不溶液-液分散广泛存在于化工、制药、食品等过程工业中。能够对不溶液-液分散进行准确描述和系统研究,对于实际过程尤其是乳化作用研究具有重要意义。不溶液-液体系指由2种或2种以上互不相溶的液体在搅拌作用下形成的一种混合物[1]。当不溶两相在叶轮的搅拌作用下混合时,一相(分散相)以液滴的形式分散到另一相(连续相)中, 同时存在着液滴的分散、聚结、悬浮以及相间的传质、传热和化学反应过程[2]。所以在实际过程中,为了保证传质、传热和化学反应过程的顺利进行,需要两相充分混合,有足够大的接触面积[3-4]。
平均液滴尺寸(MDS)和液滴尺寸分布(DSD)是描述不溶液-液体系分散程度的2个重要参数,与接触面积密切相关。MDS可以描述某个区域(点、面、体)上液滴平均尺寸,通常用d32表示,定义为:
| $ {d_{32}} = \mathop \sum \limits_{i = 1}^m {n_i}{d_i}^3/\mathop \sum \limits_{i = 1}^m {n_i}{d_i}^2 $ | (1) |
其中,n和d分别表示液滴个数和液滴直径。通过d32可以很方便地得到单位体积内两相的接触面积(S/V),其表达式为:
| $ S/V = \frac{{6\alpha }}{{{d_{32}}}} $ | (2) |
其中α表示分散相体积分数。
DSD能够反映某一区域(点、面、体)内的液滴尺寸大小分布情况,一般有2种表示形式:基于个数的液滴尺寸分布(number-DSD)或基于体积的液滴尺寸分布(volume-DSD)。其分布函数可用个数频率或体积频率表示,定义为:
| $ {{\rm{f}}_n}({d_i}) = \frac{{{n_i}}}{{\sum _{_{j = 1}}^{^m}{n_j}}}或{{\rm{f}}_v}({d_i}) = \frac{{{n_i}d_{_i}^{^3}}}{{\sum _{_{j = 1}}^{^m}{n_j}d_{_j}^{^3}}} $ | (3) |
因此如果可以获得足够多的液滴尺寸,d32、S/V、DSD就可以用方程(1)~(3)求出来。前人使用各种实验方法(照相技术[5-7],激光衍射技术[8-9],Particle Video Microscope技术[10],Focused Beam Reflectance Method Probe技术[11],相多普勒粒度分析技术[5])对不溶液-液分散体系进行了研究,得到了不同条件下的d32和DSD,并根据实验结果回归得到了许多d32的经验关联式。但实验方法的缺点是成本昂贵,测量条件和测量范围有限。有的需要搅拌槽透明,有的只能测量低浓度体系,最主要的是所有的实验方法只能给出局部范围内(某一点或者某一平面上)的d32和DSD,虽然可以通过测量多点或多个平面来减小误差,但还是不能完整描述整个搅拌槽内所有液滴的平均尺寸和分布情况。
群体平衡模型(PBM)是一种可以计算气泡和液滴尺寸分布的模型。尽管在20世纪60年代就已经出现,但由于体系复杂,方程求解困难,所以其工业应用非常有限,而且主要应用于气液体系中[12-16]。计算机的发展和计算流体动力学(CFD)方法的出现,为PBM模型的求解计算和应用提供了便利。CFD方法不仅可以克服传统实验方法的诸多缺点,还可以实现体系内部流场的可视化,得到丰富的计算数据,因而被广泛应用于固液体系、气液体系和液-液体系的混合过程。通过查阅文献,CFD方法在不溶液-液分散体系的应用研究仍然很有限。
因此,基于以上考虑,本研究采用CFD-PBM耦合的方法研究水-油分散体系在搅拌槽内的d32、S/V和DSD,同时研究叶轮转速、分散相浓度和连续相黏度对分散效果的影响。
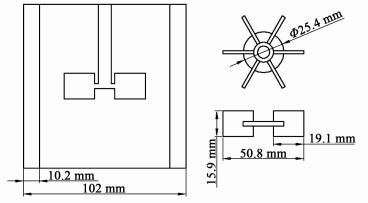
1 CFD建模 1.1 物理模型本研究模拟采用的搅拌装置如图 1所示。搅拌槽直径T=102 mm,液位高度H=T。叶轮直径D=50.8 mm,安装高度C=T/2,4块挡板垂直安装均匀分布,挡板宽度Wb=T/10。水(密度ρd=998 kg·m-3,黏度μd=0.001 Pa·s)和油(密度ρc=842 kg·m-3,黏度μc=0.003 Pa·s)分别作为分散相和连续相,两相间的界面张力σ=0.02 N·m-1。
|
| 图 1 搅拌槽结构图 Figure 1 Schematic of stirred tanks |
| |
欧拉-欧拉双流体模型用来模拟多相流动和相间作用,将每一相都当作连续的流体,并对各相分别求解连续性方程和动量方程。本研究采用的控制方程如下:
| $ \frac{\partial }{{\partial t}}{\rm{ }}({\alpha _i}{\rho _i}) + \nabla \cdot({\alpha _i}{\rho _i}{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} _i}) = 0 $ | (4) |
| $ \frac{\partial }{{\partial t}}{\rm{ }}({\alpha _i}{\rho _i}{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} _i}) + \nabla \cdot({\alpha _i}{\rho _i}{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} _i}{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} _i}) =-{\alpha _i}\nabla p + \nabla \cdot{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \tau } _i} + {\alpha _i}{\rho _i}g + {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over F} _i} $ | (5) |
其中
| $ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \tau } _i} = {\alpha _i}{\mu _i}(\nabla {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} _i} + \nabla {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} _i}^T) + {\alpha _i}({\lambda _i}-\frac{2}{3}{\mu _i})\nabla \cdot{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} _i}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over I} $ | (6) |
其中,μi和λi分别为第i相的剪切黏度和体积黏度。
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over F} = \frac{3}{4}{\alpha _{\rm{d}}}{\rho _{\rm{c}}}\frac{{{C_{\rm{D}}}}}{{{d_i}}}\left| {{u_{\rm{d}}}-{u_{\rm{c}}}} \right|({u_{\rm{d}}}-{u_{\rm{c}}}) $ | (7) |
其中,CD是曳力系数,本研究采用Schiller-Naumann模型[18],其表达式如下:
| $ \begin{array}{l} {C_{\rm{D}}} = \frac{{24(1 + 0.15R{e^{0.687}})}}{{Re}}\;\;\;\;Re \le 1000\\ {C_{\rm{D}}} = 0.44\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Re \ge 1000 \end{array} $ | (8) |
Re是相对雷诺数,定义为:
| $ Re = \frac{{{\rho _{\rm{c}}}\left| {{u_{\rm{d}}}-{u_{\rm{c}}}} \right|{d_{\rm{d}}}}}{{{\mu _{\rm{c}}}}} $ | (9) |
本研究中液相湍流采用标准k-ε模型, 该模型是针对湍流发展充分的湍流流动建立的, 也是使用最广泛的湍流模型。通过前期计算发现,该模型能够满足本研究计算要求,同时与其它两方程模型相比计算效率更高。关于湍流动能k和湍流耗散率ε所对应的输运方程表达如下:
| $ \begin{array}{c} \frac{{\partial ({\rho _{\rm{m}}}k)}}{{\partial t}} + \nabla \cdot({\rho _{\rm{m}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} }_{\rm{m}}}k) = \\ \nabla \cdot\left( {(\mu + \frac{{{\mu _{{\rm{tm}}}}}}{{{\sigma _\kappa }}})\nabla k} \right) + G-{\rho _{\rm{m}}}\varepsilon \end{array} $ | (10) |
| $ \begin{array}{c} \frac{{\partial ({\rho _{\rm{m}}}\varepsilon )}}{{\partial t}} + \nabla \cdot({\rho _{\rm{m}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} }_{\rm{m}}}\varepsilon ) = \nabla \cdot\left( {\left( {\mu + \frac{{{\mu _{{\rm{tm}}}}}}{{{\sigma _\kappa }}}} \right)\nabla \varepsilon } \right)\\ + \frac{{{C_{1\varepsilon }}\varepsilon }}{k}G + {C_{2\varepsilon }}{\rho _{\rm{m}}}\frac{{{\varepsilon ^2}}}{k} \end{array} $ | (11) |
其中G是混合相中湍流动能的产生速率。混合物的密度、速度和湍动黏度表达式如(12)~(14):
| $ {\rho _{\rm{m}}} = {\alpha _{\rm{c}}}{\rho _{\rm{c}}} + {\alpha _{\rm{d}}}{\rho _{\rm{d}}} $ | (12) |
| $ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} _{\rm{m}}} = \frac{{{\alpha _{\rm{c}}}{\rho _{\rm{c}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} }_{\rm{c}}} + {\alpha _{\rm{d}}}{\rho _{\rm{d}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over u} }_{\rm{d}}}}}{{{\alpha _{\rm{c}}}{\rho _{\rm{c}}} + {\alpha _{\rm{d}}}{\rho _{\rm{d}}}}} $ | (13) |
| $ {\mu _{{\rm{tm}}}} = \frac{{{\rho _{\rm{m}}}{C_{\rm{ \mathsf{ μ} }}}{k^2}}}{\varepsilon } $ | (14) |
更多关于湍流方程的详细描述可以参考相关文献[19]。其它模型参数分别是:C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3[20]。
1.2.3 群体平衡模型(PBM)PBM方法是描述多相流体系中分散相大小分布的通用方法。根据Tsouris和Tavlarides[21],PBM的通用形式可以表示如下:
| $ \frac{{\partial n\left( {v, t} \right)}}{{\partial t}} = {B_{\rm{B}}}\left( v \right)-{D_{\rm{B}}}\left( v \right) + {B_{\rm{C}}}\left( v \right)-{D_{\rm{C}}}\left( v \right) $ | (15) |
其中n(v, t)表示在t时刻体积为v的液滴个数,BB和BC分别指由于破碎和聚结而引起的液滴生成速率,DB和DC指由于破碎和聚结而引起的液滴消亡速率,表达式分别是:
| $ {B_{\rm{B}}} = \smallint _{_v}^{^{{v_{{{\max}}}}}}g\left( {v' } \right)\beta \left( {v, v' } \right)m\left( {v' } \right)n\left( {v', t} \right){\rm{d}}v' $ | (16) |
| $ {D_{\rm{B}}} = g{\rm{ }}\left( v \right){\rm{ }}n{\rm{ }}\left( {v, t} \right) $ | (17) |
| $ {B_{\rm{C}}} = \frac{1}{2}\smallint _{_{{v_{{\rm{min}}}}}}^{^v}a{\rm{ }}\left( {v-v', v' } \right){\rm{ }}n{\rm{ }}\left( {v-v', t} \right){\rm{ }}n{\rm{ }}\left( {v', t} \right){\rm{d}}v' $ | (18) |
| $ {D_{\rm{C}}} = \smallint _{_{{v_{{\rm{min}}}}}}^{^{v{_{\max }}}}a{\rm{ }}\left( {v, v' } \right){\rm{ }}n{\rm{ }}\left( {v, t} \right){\rm{ }}n{\rm{ }}\left( {v', t} \right){\rm{d}}v' $ | (19) |
其中,g(v)是体积为v的液滴的破碎速率,β(v, v′)是体积为v′的液滴破碎生成体积为v的液滴的概率密度函数,m(v′)是体积为v′的液滴破碎生成的子液滴数目,n(v)指t时刻体积为v的液滴数目。a(v, v′)指体积分别为v和v′的液滴碰撞发生聚结的聚结速率。关于液滴聚结破碎模型的描述有很多文献[22-26],本研究使用Turbulent-model[27-28], 和Lehr-model[14]来计算破碎速率和聚结速率。
1.3 网格划分用FLUENT前处理软件GAMBIT建立模型并划分网格。计算域分为2部分:包含叶轮的中心旋转区域和周围的静态区域。桨叶区采用非结构网格,其他区域采用结构网格,同时对叶轮区网格进行加密处理。
1.4 计算方法用离散方法求解PBM方程,计算时需要给定液滴的尺寸区间。区间数越多,预测结果越准确,计算成本也相应越大。本研究将液滴尺寸由低到高划分为15个区间,每个区间内的液滴具有相同的直径。这里使用Pacek等[29]提出的经验关联式[公式(20)]计算得到的d32作为参照,使其位于第8个区间,其它区间的液滴直径按照体积加倍或减半的规律自动生成。
| $ \frac{{{d_{32}}}}{D} = 0.052\left( {1 + 22.8\alpha } \right){\left( {\frac{{{\rho _{\rm{c}}}{N^2}{D^3}}}{\sigma }} \right)^{-0.6}} $ | (20) |
本研究采用FLUENT软件作为计算平台, 基于有限体积法,在非稳态条件下求解所有的传递方程。桨叶区采用MRF技术处理,湍流区采用k-ε标准模型,多相流模型采用Euler-Euler模型,液滴的聚结破碎用PBM模型来描述,壁面一律采用标准壁面函数处理。求解步长为0.001 s,计算步数为15 000,每次计算的最大迭代步数为30。当所有方程的残差均低于0.0001时,认为计算收敛。
2 计算结果与讨论 2.1 网格独立性验证为了确保计算的准确性,计算网格分别取8万、16万、28万、46万和63万5种精度来进行网格独立性验证。图 2给出了连续相的径向速度分量、轴向速度分量、湍流动能、分散相体积分数在叶轮附近(2r/T=0.6)的预测结果。结果显示,当网格数目超过28万时,除了湍流动能还有明显变化外,其它变量都不再随网格数的增加而发生变化。可见速度和体积分数的网格独立性容易实现,而湍流动能则需要更多的网格才能达到稳定[30-32]。图 2也表明,当网格数目达到46万时,以上4个变量都不再发生变化。此时网格数的进一步增加不会对预测结果造成影响,因此下文所有研究的网格数目都取46万。

|
| 图 2 网格独立性验证 Figure 2 Grid independence: Tangential velocity |
| |
叶轮转速(N)是搅拌混合过程中一个重要的操作参数,对不溶液-液两相的分散效果有显著影响。本研究模拟了叶轮转速分别为200、300、400、500和600 r/min条件下两相分散过程,分散相浓度为15%,结果见图 3。结果表明,随着叶轮转速的增加,d32减小,S/V增加。而且曲线log10(d32)~log10(N)和log10(S/V)~log10(N)为线性关系,相关系数均为0.9996。

|
| 图 3 d32和S/V随N的变化 Figure 3 Variation of d32 and S/V with N |
| |
分散相液滴的破碎主要是湍流压力波动作用的结果,同时液滴的内部黏性力和界面张力会阻止液滴发生破碎。转速增加会加剧湍流压力波动,从而导致越来越多的分散相液滴发生破碎。结果就是d32减小,S/V增加。Sechremeli等[4]研究了分散相体积分数低于0.1的液-液分散体系,得到了类似的结果,曲线log10(d32)~log10(N)同样呈线性关系。
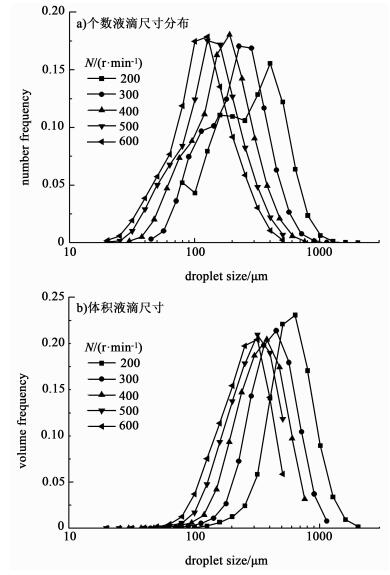
d32和S/V只能给出两相的整体分散效果,不能反映分散相液滴尺寸在不同转速条件下的分布变化。图 4给出了number-DSD和volume-DSD,结果表明,随着叶轮转速的增加,2种分布的峰值都向小尺寸方向移动。Roudsari等[33]也报道过类似的结果。图 4也表明number-DSD在200 r/min条件下呈双峰分布,随着叶轮转速的进一步增加,双峰分布逐渐变为单峰分布。以上结果与Zhou等[34]的研究结果一致,他们认为双峰分布的出现是大液滴在强旋流作用下瞬间破碎导致的。Liu等[35]认为之所以会出现双峰分布,是由于大液滴在破碎之前先被拉伸成线状,然后破碎同时产生几个小液滴所造成的。
|
| 图 4 个数液滴尺寸分布a)和体积液滴尺寸b)随N的变化 Figure 4 Variation of numberable DSD a) and volumic DSD b) with N |
| |
本研究在计算之初,假设所有液滴以相同的尺寸(区间8内的液滴直径)均匀分布在整个搅拌槽内。当叶轮转速很低时,一些液滴在重力的作用下沉入槽底,液滴尺寸分布在区间8附近形成1个峰。其余液滴在搅拌作用下分散到搅拌槽中,在叶轮附近发生破碎,此时出现了第2个峰。随着叶轮转速的增加,越来越多的液滴在叶轮搅拌作用下克服重力进入循环流动,结果使得number-DSD逐渐由双峰分布变为单峰分布。同时由于小尺寸峰值附近的液滴占所有分散相的比例很小(个数占比20%的大液滴占所有分散相体积的75%),所以volume-DSD一直呈现单峰分布。
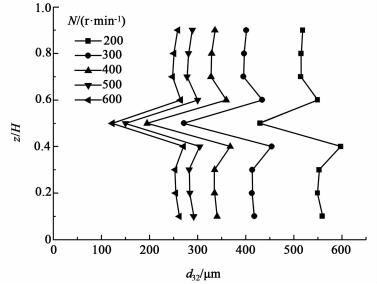
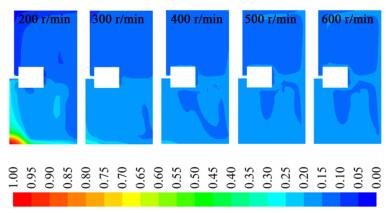
为了进一步研究分散相液滴在搅拌槽内的空间分布,沿轴向截取了9个截面(z/H=0.1~0.9),并分别计算了每个面上的d32,结果见图 5。可以看到不同叶轮转速条件下,液滴都是在z/H=0.5截面上取得最小值。这是由于该位置离叶轮最近,湍流剪切力最大,破碎占主导地位。当叶轮转速为200 r/min时,叶轮以上区域的液滴尺寸明显低于叶轮以下区域的液滴尺寸。然而,随着叶轮转速的增加,这种差距逐渐减小。当叶轮转速达到400 r/min时,差距基本消失。原因是转速较低时,分散相液滴由于重力作用沉于搅拌槽底部。较低的叶轮转速不能提供足够的能量,使液滴克服自身重力进入全槽循环中。随着转速的增加,越来越多的液滴从搅拌槽底部进入整体循环流动。当转速达到400 r/min时,分散相液滴几乎均匀分散于搅拌槽中。此时叶轮以上和叶轮以下的液滴平均尺寸几乎相同。图 6的结果也证明了这点,看到当叶轮转速达到400 r/min时,分散相基本完全分散在连续相中。
|
| 图 5 d32的轴向分布随N的变化 Figure 5 Axial distribution of d32 with N |
| |
|
| 图 6 分散相浓度云图随N的变化(α=0.15) Figure 6 Contour of dispersed phase concentration with N (α=0.15) |
| |
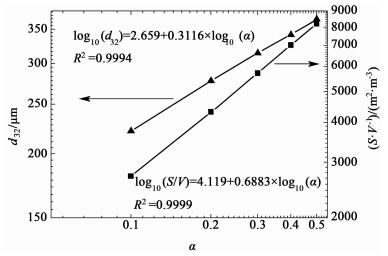
影响液-液分散效果的另一个重要的操作参数是分散相体积分数α。对于α较高的体系,实验方法的使用会受到限制。例如,LDA方法只能测量α低于3%的液滴尺寸,而CFD方法则不存在这个问题。因此为了进一步探索分散相体积分数对分散过程的影响,本研究研究了500 r/min条件下,5个分散相浓度水平(0.1~0.5)对液-液分散效果的影响。结果见图 7。
|
| 图 7 d32和S/V随α的变化 Figure 7 Variation of d32 and S/V with α |
| |
图 7表明,曲线log10(d32)~log10(α)和log10(S/V)~log10(α)都呈线性,且相关系数分别为0.9991和0.9998。当α增加时,全槽范围内的液滴平均直径d32也随之增大。原因可能是,分散相的加入增加了液滴之间的碰撞概率,有利于液滴发生聚结。图 7也表明S/V随着α的增大而增大。
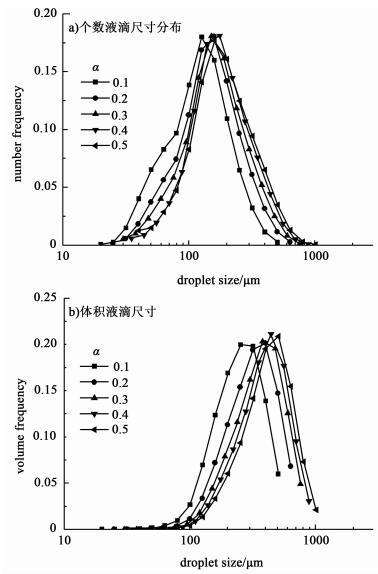
为了研究分散相体积分数对液-液的影响,图 8a)给出了500 r/min条件下number-DSD随α的变化。看到随着α的增加,number-DSD向小尺寸方向移动,但是变化并不明显。Roudsari等[34]也做了类似的研究,发现在300 r/min条件下,分散相体积分别为0.15和0.25时的分散效果没有明显的差别。还有许多研究者[10, 36-37]也得到了类似的结果。然而,图 8b)表明,随着α的增加,volume-DSD发生了明显的变化。结果表明,与全槽范围内的d32一样,整体液滴尺寸分布也是随着α的增大而增大。
|
| 图 8 个数液滴尺寸分布a)和体积液滴尺寸分布b)随α的变化 Figure 8 Variation of numberable DSD a) and volumic DSD b) with α |
| |
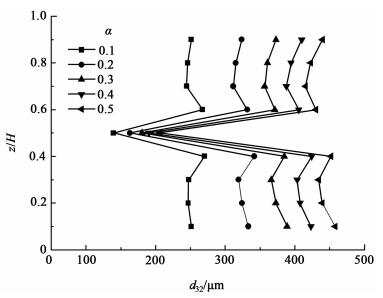
图 9展示了α对液滴在搅拌槽内空间分布的影响。
|
| 图 9 d32的轴向分布随α的变化 Figure 9 Variation of axial distribution of d32 with α |
| |
图 9表明,随着α的增大,各截面上的d32都增大。当α较低时,叶轮以下区域和叶轮以上区域各截面上的d32基本相同。随着α的增加,叶轮以上区域和叶轮以下区域各截面上的d32开始出现差异。原因是部分分散相在重力作用下沉在搅拌槽底部,使得两相混合不均匀导致的。图 10也证明了这一点。

|
| 图 10 分散相浓度云图随α的变化(N=500 r/min) Figure 10 Contour of dispersed phase concentration with α (N=500 r/min) |
| |
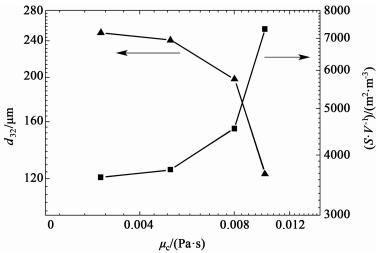
在混合过程中,机械能通过叶轮传递给流体,使得流体发生湍流波动,最终以漩涡的形式耗散掉。能量依次从最大的漩涡传递到最小的漩涡,最后在小漩涡内部通过黏性相互作用耗散掉。图 11展示了N=500 r/min、α=0.15条件下,4个连续相黏度(μc=0.003、0.005、0.008和0.010 Pa·s)对分散过程的影响。结果表明,随着μc的增大,d32减小,S/V增大。曲线log10(d32)~log10(μc)和log10(S/V)~log10(μc)不再呈现线性关系。
|
| 图 11 d32和S/V随μc的变化 Figure 11 Variation of d32 and S/V with μc |
| |
根据文献[38-39]知道,湍流区可以分为2个区域:湍流惯性区和湍流黏性区。在湍流惯性区内,液滴尺寸大于最小漩涡尺寸,此时湍流剪切力占主导地位;在湍流黏性区内,液滴尺寸小于最小液滴尺寸,此时黏性剪切力对液滴的破碎起主导作用。一方面,随着连续相黏度的增加,黏性剪切力增加,更多的液滴会发生破碎。另一方面,连续相黏度的增大会阻碍液滴之间的碰撞,从而降低液滴的聚结速率。这两方面作用的结果就是d32的减小和S/V的增大。
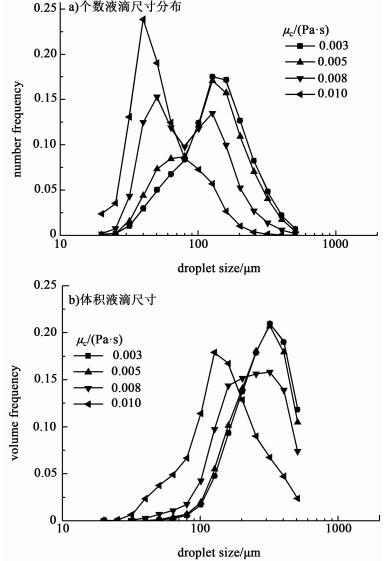
图 12表明随着μc的增大,分散相的2种液滴尺寸分布都向小尺寸方向偏移。Number-DSD先由单峰变为双峰,后又变为单峰。而volume-DSD则没有这种变化,一直保持单峰分布。合理的解释可能是,μc的增大使得黏性剪切力增大,大液滴破碎成许多小液滴,使得number-DSD出现了双峰。随着μc的进一步增大,越来越多的大液滴在黏性剪切力的作用下破碎生成小液滴,最终使得number-DSD又变为单峰。这里液滴尺寸分布的变化类似于前面2.2中N=200 r/min时的情况。
|
| 图 12 个数液滴尺寸分布a)和体积液滴尺寸b)随μc的变化 Figure 12 Variation of numberable DSD a) and volumic DSD b) with μc |
| |
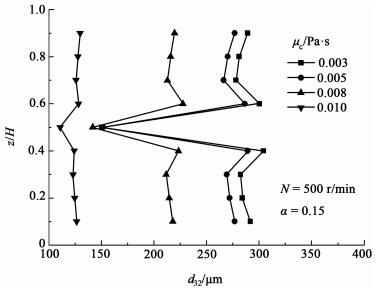
不同黏度条件下液滴的空间尺寸分布见图 13,结果表明,不同截面上的d32随着μc的增加急剧减小,这是由于湍流黏性力增大导致的。结果同时表明d32沿轴向在全槽范围内越来越均匀。可见,连续相黏度对液滴分散效果具有显著影响。对于转速固定的液-液分散过程,可以通过改变连续相黏度来实现更好的分散。
|
| 图 13 d32的轴向分布随μc的变化 Figure 13 Variation of axial distribution of d32 with μc |
| |
使用CFD-PBM耦合方法研究了不溶液-液两相在搅拌槽内的混合分散过程。用MFR技术模拟叶轮旋转,使用基于欧拉-欧拉方法的k-ε模型模拟湍流流动。用基于离散方法求解的PBM方程描述液滴的破碎聚结过程。详细研究了叶轮转速、分散相体积分数、连续相黏度对d32、S/V和DSD的影响,主要结论有:
1) N增大时,d32减小,S/V增大,number-DSD从双峰变为单峰分布,volume-DSD则始终保持单峰。曲线log10(d32)~log10(N)和log10(S/V)~ log10(N)均为线性关系,相关系数都是0.9996。
2) α增大时,d32和S/V都增大,2种DSD始终保持单峰分布。曲线log10(d32)~log10(α)和log10(S/V)~log10(α)同样为线性关系,相关系数分别是0.9991和0.9998。
3) μc增大时,d32减小,S/V增大,number-DSD先从单峰变为双峰,后又变为单峰,volume-DSD则始终保持单峰分布。
4) CFD方法可以用于研究不溶液-液体系的混合分散过程,能够给出全槽范围内的液滴平均尺寸和液滴尺寸分布,能够对分散过程进行相对全面的描述,弥补了实验方法的不足。
符号说明:
a(v, v′)—体积分别为v和v′的液滴碰撞发生聚结的概率;
BB—破碎引起的液滴生成速率,1/s;
BC—聚结引起的液滴生成速率,1/s;
C—叶轮安装高度,m;
CD—湍流中的曳力系数;
d—液滴直径,m;
d32—平均液滴直径,m;
D—搅拌桨直径,m;
DB—破碎引起的液滴消亡速率,1/s;
DC—聚结引起的液滴消亡速率,1/s;
F—相间作用力,N/m3;
fn—个数频率;
fv—体积频率;
F—相间作用力,N/m3;
g—重力加速度,m/s2;
g(v)—体积为v的液滴发生破碎的概率;
H—液位高度,m;
I—单位张量;
k—湍动能,m2/s2;
N—叶轮转速,r/min;
n—液滴个数;
p—压力,Pa;
Re—雷诺数;
S—不溶液-液两相接触面积,m2;
t—时间,s;
T—搅拌槽直径,m;
u—速度,m/s;
V—搅拌装置体积,m3;
Wb—挡板宽度,m;
α—分散相体积分数;
β(v, v′)—体积为v′的液滴破碎生成体积为v的液滴的概率密度函数;
ε—湍流耗散速率,m2/s3;
ρ—密度,kg/m3;
μ—黏度,Pa·s;
τ—应力,N/m;
σ—表面张力,N/m。
| [1] | Luo H, Svendsen H F. Theoretical model for drop and bubble breakup in turbulent dispersions[J]. AIChE Journal, 1996, 42(5): 1225–1233. DOI: 10.1002/(ISSN)1547-5905 |
| [2] | Edward L P, Atiemo-Obeng V A, Kresta M S. Handbook of industrial mixing:Science and practice[M]. New Jersey: John Wiley & Sons, Inc, 2004. |
| [3] | Eastwood C D, Armi L, Lasheras J C. The breakup of immiscible fluids in turbulent flows[J]. Journal of Fluid Mechanics, 2004, 502: 309–333. DOI: 10.1017/S0022112003007730 |
| [4] | Sechremeli D, Stampouli A, Stamatoudis M. Comparison of mean drop sizes and drop size distributions in agitated liquid-liquid dispersions produced by disk and open type impellers[J]. Chemical Engineering Journal, 2006, 117(2): 117–122. DOI: 10.1016/j.cej.2005.12.015 |
| [5] | Chen H T, Middleman S. Drop size distribution in agitated liquid-liquid systems[J]. AIChE Journal, 1967, 13(5): 989–998. DOI: 10.1002/(ISSN)1547-5905 |
| [6] | Calabrese R V, Wang C, Bryner N P. Drop breakup in turbulent stirred-tank contactors:Ⅲ. Correlations for mean size and drop size distribution[J]. AIChE Journal, 1986, 32(4): 677–681. DOI: 10.1002/(ISSN)1547-5905 |
| [7] | Wang C, Calabrese R V. Drop breakup in turbulent stirred-tank contactors:Ⅱ. Relative influence of viscosity and interfacial tension[J]. AIChE Journal, 1986, 32(4): 667–676. DOI: 10.1002/(ISSN)1547-5905 |
| [8] | Desnoyer C, Masbernat O, Gourdon C. Experimental study of drop size distributions at high phase ratio in liquid-liquid dispersions[J]. Chemical Engineering Science, 2003, 58(7): 1353–1363. DOI: 10.1016/S0009-2509(02)00461-X |
| [9] | El-Hamouz A, Cooke M, Kowalski A, et al. Dispersion of silicone oil in water surfactant solution:Effect of impeller speed, oil viscosity and addition point on drop size distribution[J]. Chemical Engineering and Processing, 2009, 48(2): 633–642. DOI: 10.1016/j.cep.2008.07.008 |
| [10] | Boxall J A, Koh C A, Sloan E D, et al. Measurement and calibration of droplet size distributions in water-in-oil emulsions by particle video microscope and a focused beam reflectance method[J]. Industrial & Engineering Chemistry Research, 2010, 49: 1412–1418. |
| [11] | Wang W, Chen W, Duan J, et al. Effect of dispersed holdup on drop size distribution in oil-water dispersions:Experimental observations and population balance modeling[J]. Chemical Engineering Science, 2014, 105: 22–31. DOI: 10.1016/j.ces.2013.10.012 |
| [12] | Colella D, Vinci D, Bagatin R, et al. A study on coalescence and breakage mechanisms in three different bubble columns[J]. Chemical Engineering Science, 1990, 54: 4767–4777. |
| [13] | Olmos E, Gentric C, Vial C, et al. Numerical simulation of multiphase flow in bubble column reactors:Influence of bubble coalescence and breakup[J]. Chemical Engineering Science, 2001, 56: 6359–6365. DOI: 10.1016/S0009-2509(01)00204-4 |
| [14] | Lehr F, Millies M, Mewes D. Bubble-Size distributions and flow fields in bubble columns[J]. AIChE Journal, 2002, 48: 2426–2443. DOI: 10.1002/(ISSN)1547-5905 |
| [15] | Ramkrishna D, Mahoney A W. Population balance modeling. Promise for the future[J]. Chemical Engineering Science, 2002, 57: 595–606. DOI: 10.1016/S0009-2509(01)00386-4 |
| [16] | Chen P, Sanyal J, Dudukovic M P. Numerical simulation of bubble columns flows:Effect of different breakup and coalescence closures[J]. Chemical Engineering Science, 2005, 60: 1085–1101. DOI: 10.1016/j.ces.2004.09.070 |
| [17] | Ljungqvist M, Rasmuson A. Numerical simulation of the two phase flow in an axially stirred reactor[J]. Chemical Engineering Research and Design, 2001, 79: 533–546. DOI: 10.1205/02638760152424307 |
| [18] | Schiller L, Naumann A. A drag coefficient correlation[J]. Z Ver Deutsch Ing, 1935, 77: 318–325. |
| [19] | Kasat G R, Khopkar A R, Ranade V V, et al. CFD simulation of liquid-phase mixing in solid-liquid stirred reactor[J]. Chemical Engineering Science, 2008, 63: 3877–3885. DOI: 10.1016/j.ces.2008.04.018 |
| [20] | Blazek J. Computational fluid dynamics:Principles and applications[M]. Amsterdam: Elsevier Ltd., 2005. |
| [21] | Tsouris C, Tavlarides L L. Breakup and coalescence models for drops in turbulent dispersions[J]. AIChE Journal, 1994, 40: 395–406. DOI: 10.1002/(ISSN)1547-5905 |
| [22] | Alopaeus V, Koskinen J, Keskinen K I. Simulation of the population balances for liquid-liquid systems in a non ideal stirred tank. Part 1.Description and qualitative validation of the model[J]. Chemical Engineering Science, 1999, 54: 5887–5899. DOI: 10.1016/S0009-2509(99)00170-0 |
| [23] | Lasheras J C, Eastwood C, Martinez-Bazan C, et al. A review of statistical models for the break-up of an immiscible fluid immersed into a fully developed turbulent flow[J]. International Journal of Multiphase Flow, 2002, 28: 247–278. DOI: 10.1016/S0301-9322(01)00046-5 |
| [24] | Liao Y, Lucas D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions[J]. Chemical Engineering Science, 2009, 64: 3389–3406. DOI: 10.1016/j.ces.2009.04.026 |
| [25] | Wang T, Wang J, Jin Y. A novel theoretical breakup kernel function for bubbles/droplets in a turbulent flow[J]. Chemical Engineering Science, 2003, 58: 4629–4637. DOI: 10.1016/j.ces.2003.07.009 |
| [26] | Liao Y, Lucas D. A literature review on mechanisms and models for the coalescence process of fluid particles[J]. Chemical Engineering Science, 2010, 65: 2851–2864. DOI: 10.1016/j.ces.2010.02.020 |
| [27] | Abrahamson J. Collision rates of small particles in a vigorously turbulent fluid[J]. Chemical Engineering Science, 1975, 30: 1371–1379. DOI: 10.1016/0009-2509(75)85067-6 |
| [28] | Higashitani K, Yamauchi K, Matsuno Y, et al. Turbulent coagulation of particles dispersed in a viscous fluid[J]. Journal of Chemical Engineering of Japan, 1983, 16(4): 299–304. DOI: 10.1252/jcej.16.299 |
| [29] | Pacek A W, Man C C, Nienow A W. On the Sauter mean diameter and size distributions in turbulent liquid-liquid dispersions in a stirred vessel[J]. Chemical Engineering Science, 1998, 53: 2005–2011. DOI: 10.1016/S0009-2509(98)00068-2 |
| [30] | Deglon D A, Meyer C J. CFD modeling of stirred tanks:Numerical considerations[J]. Minerals Engineering, 2006, 19: 1059–1068. DOI: 10.1016/j.mineng.2006.04.001 |
| [31] | Feng X, Cheng J, Li X, et al. Numerical simulation of turbulent flow in a baffled stirred tank with an explicit algebraic stress model[J]. Chemical Engineering Science, 2012, 69: 30–44. DOI: 10.1016/j.ces.2011.09.055 |
| [32] | Feng X, Li X, Cheng J, et al. Numerical simulation of solid-liquid turbulent flow in a stirred tank with a two-phase explicit algebraic stress model[J]. Chemical Engineering Science, 2012, 82: 272–284. DOI: 10.1016/j.ces.2012.07.044 |
| [33] | Roudsari S F, Turcotte G, Dhib R, et al. CFD modeling of the mixing of water in oil emulsions[J]. Computers & Chemical Engineering, 2012, 45: 124–136. |
| [34] | Zhou G, Kresta S M. Evolution of drop size distribution in liquid-liquid dispersions for various impellers[J]. Chemical Engineering Science, 1998, 53(11): 2099–2113. DOI: 10.1016/S0009-2509(97)00437-5 |
| [35] | Liu C, Li M, Liang C, et al. Measurement and analysis of bimodal drop size distribution in a rotor-stator homogenizer[J]. Chemical Engineering Science, 2013, 102: 622–631. DOI: 10.1016/j.ces.2013.08.030 |
| [36] | Ruiz M C, Lermanda P, Padilla R. Drop size distribution in a batch mixer under breakage conditions[J]. Hydrometallurgy, 2002, 63: 65–74. DOI: 10.1016/S0304-386X(01)00223-7 |
| [37] | Vankova N, Tcholakova S, Denkov N D, et al. Emulsification in turbulent flow. 1. Mean and maximum drop diameters in inertial and viscous regimes[J]. Journal of Colloid and Interface Science, 2007, 312: 363–380. DOI: 10.1016/j.jcis.2007.03.059 |
| [38] | Stamatoudis M, Tavlarides L L. The effect of continuous-phase viscosity on the unsteady state behavior of liquid-liquid agitated dispersions[J]. Chemical Engineering Journal, 2007, 35: 137–143. |
| [39] | Vankova N, Tcholakova S, Denkov N D, et al. Emulsification in turbulent flow. 1. Mean and maximum drop diameters in inertial and viscous regimes[J]. Journal of Colloid and Interface Science, 2007, 312: 363–380. DOI: 10.1016/j.jcis.2007.03.059 |
 2018, Vol. 35
2018, Vol. 35





