2. 海申机电总厂(象山), 江苏宁波 315718
2. Haishen Machinery & Electric General Works, Jiangsu Ningbo 315718, China
卧式螺旋沉降离心机(下简称卧螺离心机),是一种高效的离心分离设备,广泛应用在石油、化工、冶金、煤炭等工业部门和污水处理工程等领域[1-2]。在聚合树脂领域,卧螺离心机处理聚氯乙烯(PVC)的能力最大可达到18 t/h(以干粉计);在煤化工领域,卧螺离心机可处理存在三相物质(氨水、煤焦油和焦渣)的煤焦油回收液;在非金属矿领域,卧螺离心机可用于钛白、高岭土、碳酸钙、珍珠粉等的分级处理。在卧螺离心机流场研究方面,已有不少学者采用有限元软件获得其速度场、压力场分布及运动规律[3-4];在卧螺离心机静力学方面,也有不少学者采用有限元软件分别对转鼓、螺旋输送器进行强度刚度校核及优化设计[5-7];在卧螺离心机动力特性方面,其有限元模型也从一维耦合模型发展到复杂的三维耦合模型[8-10]。
本研究采用有限元分析方法,模拟得到卧螺离心机物料为清水时流场的压力分布,结合结构静力学分析考察了卧螺离心机转子系的应力、应变分布规律,最后通过预应力结构动力学分析对物料作用下的卧螺离心机动力特性进行研究,并通过振动测试试验验证了有限元模拟的准确性。研究结果为大型卧螺离心机的结构优化设计和改进提供参考与依据。
1 几何模型以某大型卧螺离心机为研究对象,该卧螺离心机主要由转鼓、螺旋输送器、差速器、主副电机以及机座组成。考虑到卧螺离心机转子系双转子结构的复杂性,对模型进行一定的简化[9]:忽略内外转子的螺栓连接,将螺栓连接起来的部件看成一个整体;不考虑轴承非线性油膜力的影响,认为轴承是各向同性的,刚度为常数;不考虑系统材料阻尼的影响;差速器跟电机简化为质量点;物料的质量基于刚体动力学原理,采用转动惯量等效的方法进行转换[10],转换过程中保持转鼓的结构不变,根据运行过程中物料的分布,增加转鼓相应部分的密度,保证密度增加后转鼓的转动惯量等于转换前转鼓与物料转动惯量之和来现实转动惯量的转换。简化后其转子系模型如图 1所示。

|
| 图 1 卧螺离心机转子系结构简图 Figure 1 The structure of decanter centrifuge |
| |
随着我国基础工业的快速进步和分离技术的迅速发展,卧螺离心机也日臻高转速化、高参数化和大容量化,其受到物料及其它激励源作用而产生的振动问题也日益突出,因此有必要考虑物料作用对卧螺离心机的影响并进行相应流固耦合研究和分析。
2.1 基本假设对于卧螺离心机来说,转鼓内壁面及螺旋叶片受到物料作用后其变形量较小,故不考虑结构场变化对流体场的影响,仅把流体场计算结果传递给固体结构,做单向流固耦合分析,并做出以下假设:流体为不可压缩流体,固体结构为各向同性线弹性。
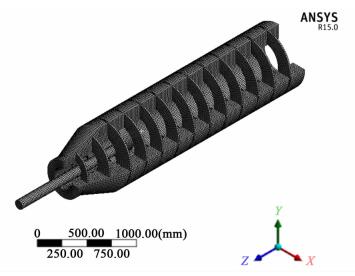
2.2 计算模型及边界条件分别建立流体计算域和结构计算域的三维有限元模型如图 2和图 3所示。为了保证流体计算域所得载荷能精确的传递到流固耦合交界面上,将流体计算域和结构计算域在各自求解器中的坐标系保持一致。
|
| 图 2 离心机流场有限元模型(半剖图) Figure 2 The finite element model of flow field(half-cutaway) |
| |

|
| 图 3 卧螺离心机有限元模型 Figure 3 The finite element model of decanter centrifuge |
| |
卧螺离心机流体计算域的介质为常温水,湍流流动状态,采用SST湍流模型计算,使用自动壁面函数以考虑边界层的影响,进口流量为1.94 kg/s,方向垂直于入口,出口边界则为压力出口,相对压力为0,旋转壁面设为无滑移边界条件,而自由液面设为自由滑移边界[11],螺旋叶片以immersed solid的形式考虑到流场中。卧螺离心机结构计算域各部件采用solid186单元模拟,螺旋输送器与转鼓、转鼓与机座之间的轴承连接采用cmbin214单元模拟,机座下方的减振器则采用combin14单元模拟。螺旋输送器与转鼓、转鼓与机座之间通过滚动轴承连接,式(1)和式(2)为轴承刚度计算公式,采用基于赫兹理论的半经验公式法[12]。
| $ {k_{\rm{s}}} = 37190z\delta _{\rm{r}}^{^{1/2}}D_{\rm{b}}^{^{1/2}} $ | (1) |
| $ {k_{\rm{c}}} = 10131z\delta _{\rm{r}}^{^{1/9}}l_{_{{\rm{we}}}}^{^{0.889}} $ | (2) |
式(1)和式(2)中:ks为深沟球轴承刚度;kc为圆柱滚子轴承刚度;z为滚子数;δr为轴承径向变形;Db为球滚子直径;lwe为圆柱滚子有效长度。
计算得到卧螺离心机各轴承刚度如表 1所示。
| 轴承 | 主轴承 | 中介轴承 | ||
| 小端 | 大端 | 小端 | 大端 | |
| 轴承刚度/(N·m-1) | 5.5×108 | 4.9×109 | 1.3×109 | 1.3×109 |
卧螺离心机结构计算域各部件的材料特性常数如表 2所示。
| 部件 | 弹性模量/GPa | 泊松比 | 密度/(kg·m-3) |
| 转鼓 | 190 | 0.3 | 7 880 |
| 螺旋 | 200 | 0.3 | 8 000 |
| 机座 | 210 | 0.3 | 7 850 |
卧螺离心机在负载工况下运行,转鼓转动带动物料一同旋转。然而,物料的旋转和转鼓的旋转并不一致,存在滞后现象,其中物料的滞后量可由式(3)得到。同时,转鼓内壁面会受到物料的离心液压力,式(4)为离心液压的理论计算公式。
| $ \omega /{\omega _0} = 1-\left( {1-\frac{{\omega ' }}{{{\omega _0}}}} \right)\frac{{k_{_0}^{^{-2}} - 1}}{{{k^{ - 2}} - 1}} $ | (3) |
| $ p = \frac{1}{2}{\rho _1}\omega _{_0}^{^2}({r^2}-r_{_1}^{^2}) $ | (4) |
式(3)和式(4)中:ω′为自由液面处角速度;ω0为转鼓角速度;k0为液面任意处湍动能;k为转鼓一定转速下的最大湍动能;p为离心液压;ρ1为物料密度;r为转鼓半径;r1为物料环内表面半径。
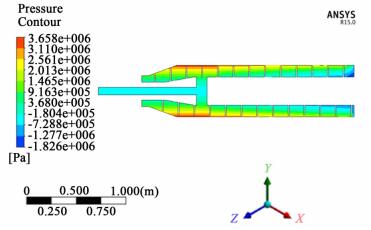
当转速为3 000 r/min时,YZ截面的流场压力分布云图如图 4所示。
|
| 图 4 流场压力分布云图 Figure 4 The flow field pressure distribution nephogram |
| |
从图 4可以看出,流场压力沿着半径方向从自由液面到转鼓内壁面逐渐增大,其中最大压力位于进料分布器出口段的转鼓内壁面处。
图 5和图 6分别为周向速度滞后量随转速变化关系图和离心液压随转速变化关系图。

|
| 图 5 滞后量ω/ω0随转速变化关系 Figure 5 Hysteresis ω/ω0 versus rotational speed |
| |
|
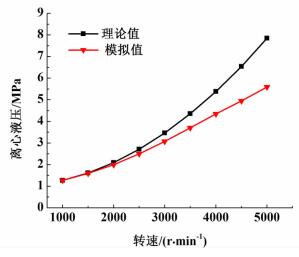
| 图 6 离心液压随转速变化关系 Figure 6 Centrifugal hydraulic pressure versus rotational speed |
| |
从图 5可以看出,随着转速的增加,周向速度滞后值逐渐增加,主要是因为物料随着转速的增加获得加速的时间也相对增长,并且模拟值比理论值略高。
从图 6中可以看出,随着转速的增加,转鼓内壁所受的离心液压也增大,同时模拟液压与理论液压的差值也越来越大,当转速为3 000 r/min时理论液压值为3.46 MPa而模拟液压值为3.08 MPa,模拟值占理论值的89.02%。这是因为液体与转鼓之间存在滞后现象,而液压与转速成平方关系,转速越大,滞后现象越明显。
3.2 转子系流固耦合分析提取转鼓内壁面以及螺旋叶片上的压力导入ANSYS静力学模块做离心力作用下的单向流固耦合静力学分析。图 7为转子系在正常工况工作转速3 000 r/min下的静力学分析云图。

|
| 图 7 转子系正常工况下静力学分析结果 Figure 7 The statics analysis results of the rotor system under load condition |
| |
从图 7可以看出,转子系最大位移发生在螺旋输送器中部,为0.58 mm;最大应力则位于螺旋筒体中部与螺旋叶片根部连接处,属于局部应力,为154.38 MPa。由此可知,卧螺离心机在正常工况下满足强度刚度要求,同时在螺旋输送器制造过程中可适当增加螺旋叶片根部的焊脚高度来降低该处应力以防止叶片断裂破坏事故的发生。
3.3 整机动力学特性分析将静力学分析结果作为预应力进行预应力模态分析,通过设置coriolis effect来考虑陀螺效应,采用QR阻尼法来求解,得到卧螺离心机整机的前八阶临界转速如表 3所示。
| 阶数 | 一阶 | 二阶 | 三阶 | 四阶 | 五阶 | 六阶 | 七阶 | 八阶 |
| 转速/(r·min-1) | 245.4 | 255.8 | 278.3 | 286.4 | 426.2 | 456.1 | 4 432.8 | 5 219.4 |
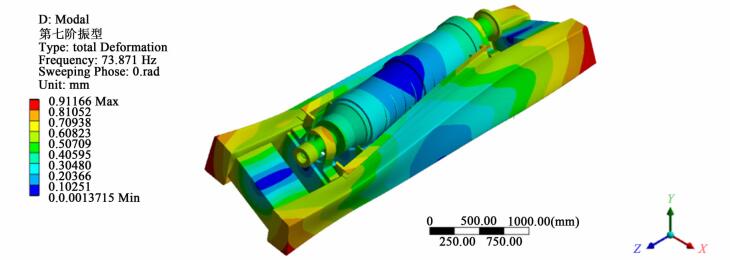
从表 3可看出,前六阶临界转速很低,在离心机启动过程中快速越过此共振区而不会发生结构共振,现取所关注的第七阶跟第八阶振型加以分析,分别见图 8和图 9。
|
| 图 8 卧螺离心机七阶振型图 Figure 8 The seventh order vibration mode of decanter |
| |
|
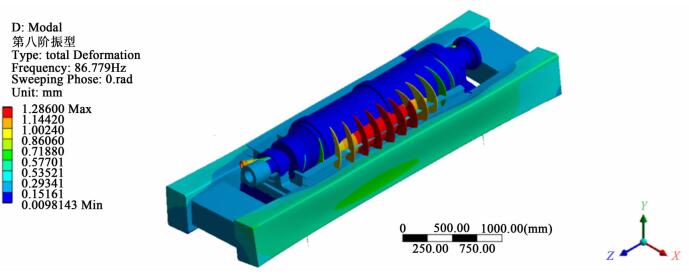
| 图 9 卧螺离心机八阶振型图 Figure 9 The eighth order vibration mode of decanter |
| |
从图 8可以看出,在机座激励下,卧螺离心机整机的七阶模态振型主要是机座绕着中轴线的扭转振动,位移最大处发生在机座四角,转子系并没有被激励起,随着机座一起发生扭转振动。
卧螺离心机的第八阶模态振型如图 9所示,整机以绕着中轴线的摆动振型为主,同时螺旋被激励起,在水平面上发生横向弯曲振动。由模态分析可知,随着激励频率的提高,依次发生振动的是机座、螺旋和转鼓。卧螺离心机正常工况下转速为3 000 r/min,即激励频率为50 Hz,在此频率下,整机不会发生结构共振。同时,针对第七阶模态振型改造机座结构优化机座刚度可有效提高卧螺离心机的临界转速。
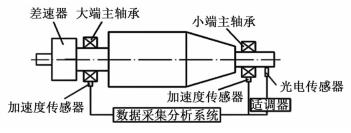
4 振动测试试验为了验证模拟的准确性,对该型号卧螺离心机进行现场振动测试试验。所用的传感器为反射式光电传感器和压电式加速度传感器,光电传感器用于测量转速,加速度传感器采集到两端轴承座的振动加速度值并经积分后得到振动速度,测试流程如图 10所示。
|
| 图 10 测试流场图 Figure 10 Flow chart of the vibration test |
| |
工程中,常用敲击脉冲法测试设备的固有频率[13],但实际试验过程中,对于此大型的卧螺离心机,敲击并不能很好地激励起高阶的整机衰减振动,而且静止状态下测试所得的固有频率也不能很好地反映负载工况下的临界转速。针对卧螺离心机独特的双转子结构,螺旋输送器截面惯性矩不相等,卧螺离心机启动过程中,在重力作用下,达到第一临界转速的一半附近可测到1个振动小峰值,并对应着2倍频振动。可由此测定卧螺离心机的临界转速而避免直接在临界转速运转状态下测定,该转速常称为副临界转速[14]。
测量并记录下卧螺离心机开机后转速从0~3 200 r/min大小两端主轴承座的振动速度数据,其中小端轴承座水平方向所测得开机过程的振动速度时域图及频谱图如图 11所示。
|
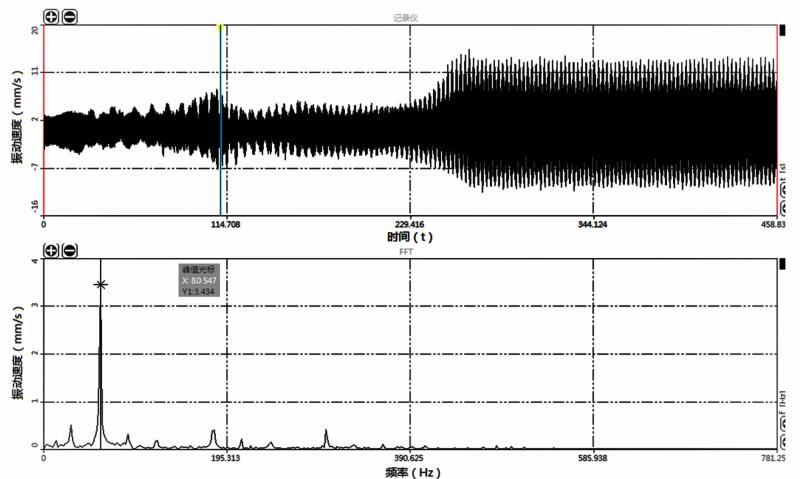
| 图 11 小端轴承水平方向振动响应(2 200 r/min) Figure 11 The small end bearing horizontal vibration response (2 200 r/min) |
| |
从图 11的时域波形图中可以看出,卧螺离心机转速从0~3 200 r/min过程中,在114.7 s附近出现一个振动小峰值,对该峰值段进行FFT快速傅里叶变化便可得到相应的频谱图,该转速下振动频率为80.55 Hz(4 833 r/min),以2倍频振动为主,振动速度峰值为3.43 mm/s。由此可知,该转速为卧螺离心机的副临界转速,振动频率对应的转速4 833 r/min可粗略的认为是卧螺离心机的临界转速。
离心机整机负载工况下,两端轴承水平方向的振动烈度随转速变化如图 12所示。
|
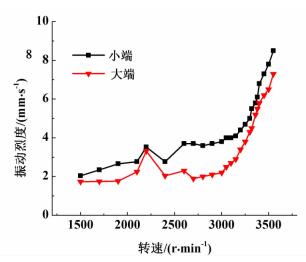
| 图 12 振动烈度随转速变化关系 Figure 12 Vibration intensity versus rotational speed |
| |
从图 12可知,大小两端在2 200 r/min附近均出现了振动小峰值,与图 11中的时域图相一致。进一步确定转速4 833 r/min为该卧螺离心机的副临界转速[15],而数值模拟得到的卧螺离心机由螺旋激励引起的临界转速为5 219.4 r/min,与测试结果差别为7.4%,误差范围内可认为数值模拟计算是准确可靠的。因此,实际工程中可通过测定卧螺离心机的副临界转速来测定卧螺离心机的临界转速。
5 结论1) 随着转速的提高,周向速度的滞后量缓慢增大,转鼓内壁所受离心液压快速增大,同时模拟液压与理论液压的差值逐渐增大。卧螺离心机在正常工况下,转子系最大位移发生在螺旋中部,为0.58 mm;最大应力位于螺旋叶片根部与螺旋筒体连接处,为154.38 MPa,强度刚度均满足工况要求。
2) 卧螺离心机在正常工况下,从启动到工作转速会经历六阶振型,但随着转速的快速提高,振动会消失。卧螺离心机在正常工况时的频率为50 Hz,不会发生共振。
3) 随着转速的提高,卧螺离心机发生振动的依次是机座、螺旋、转鼓,即离心机重要部件的刚度由低到高依次为机座、螺旋、转鼓。因此针对整机的七阶模态振型对机座结构进行优化可提高卧螺离心机的临界转速。
4) 实际工程中可通过测定卧螺离心机的副临界转速来测定卧螺离心机的临界转速,避免直接在临界转速运转状态下测定,为卧螺离心机临界转速的测定提供方法。
| [1] |
孙启才, 金鼎五.
离心机原理结构与设计计算[M]. 北京: 机械设计出版社, 1987 Sun Qicai, Jin Dingwu. The centrifuge principle structure and design calculation[M]. Beijing: Mechanical Design Press, 1987. |
| [2] | Bell G R A, Symons D D, Pearse J R. Mathematical model for solids transport power in a decanter centrifuge[J]. Chemical Engineering Science, 2014, 107(14): 114–122. |
| [3] |
于萍, 林苇, 王晓彬, 等. 卧螺离心机离心分离场速度仿真分析[J].
机械工程学报, 2011, 24: 151–157.
Yu Ping, Lin Wei, Wang Xiaobin, et al. Velocity simulation analysis on centrifuge separation field of horizontal spiral centrifuge[J]. Journal of Mechanical Engineering, 2011, 24: 151–157. |
| [4] |
董连东, 付双成, 袁惠新. 卧螺离心机内压力场的数值模拟[J].
化工进展, 2014, 2: 309–313, 336.
Dong Liandong, Fu Shuangcheng, Yuan Huixin. Numerical simulation on pressure field in a decanter centrifuge[J]. Chemical Industry and Engineering Progress, 2014, 2: 309–313, 336. |
| [5] |
李龙. LWS400卧螺离心机参数变化对转鼓强度和刚度的影响[J].
当代化工, 2014, 11: 2346–2349, 2357.
Li Long. Influence of parameters changing of LWS400 horizontal spiral centrifuge on the strength and stiffness of the rotating drum[J]. Contemporary Chemical Industry, 2014, 11: 2346–2349, 2357. DOI: 10.3969/j.issn.1671-0460.2014.11.043 |
| [6] | Chiang H W D, Hsu C N, Tu S H. Rotor-Bearing analysis for turbomachinery single and dual-rotor systems[J]. Journal of Propulsion and Power, 2004, 20(6): 1096–1104. |
| [7] |
杨钊, 黄维菊, 高志惠, 等. 大长径比卧螺离心机螺旋输送器的有限元分析[J].
过滤与分离, 2011, 4: 13–19.
Yang Zhao, Huang Weiju, Gao Zhihui, et al. Finite element analysis of screw conveyor of horizontal screw centrifuge with large aspect ratio[J]. Journal of Filtration and Separation, 2011, 4: 13–19. DOI: 10.3969/j.issn.1005-8265.2011.04.004 |
| [8] | Mihail B, Teodor S, Aurel A. Flexion movement analysis of horizontal centrifuges rotors having the basket between the bearings[D]. Bucharest: Politehnica University of Bucharest, 2010 https://www.researchgate.net/publication/290080907_Flexion_Movement_Analysis_of_Horizontal_Centrifuges_Rotors_Having_the_Basket_Between_the_Bearings |
| [9] |
张晓军, 张志新, 贺世正, 等. 卧螺离心机转子动力特性计算[J].
流体机械, 2007(5): 47–49, 28.
Zhang Xiaojun, Zhang Zhixin, He Shizheng, et al. Rotor dynamic characteristic calculation of the horizontal helical-conveyer centrifuge[J]. Fluid Machinery, 2007(5): 47–49, 28. |
| [10] |
应超, 孙恒, 王东琪, 等. 大型卧式螺旋卸料沉降离心机转子动力学分析[J].
化工设备与管道, 2014, 51(2): 38–42.
Ying Chao, Sun Heng, Wang Dongqi, et al. Dynamics analysis for rotor in large decanter centrifuge[J]. Process Equipment and Piping, 2014, 51(2): 38–42. |
| [11] |
黄志新, 钱才富, 范德顺, 等. 沉降离心机圆形转鼓内液面速率的数值模拟[J].
北京化工大学学报:自然科学版, 2007, 34(6): 645–648.
Huang Zhixin, Qian Caifu, Fan Deshun, et al. Numerical simulation of the velocity of the fluid surface in the bowl of a sedimentation centrifuge[J]. Journal of Beijing University of Chemical Technology(Natural Science Edition), 2007, 34(6): 645–648. |
| [12] |
刘泽九.
滚动轴承应用手册[M]. 北京: 机械工业出版社, 2006 Liu Zejiu. Rolling bearing application manual[M]. Beijing: China Machine Press, 2006. |
| [13] |
卢双龙, 孙丹, 杨建刚. 某型卧螺离心机振动测试与分析[J].
流体机械, 2009(4): 5–8.
Lu Shuanglong, Sun Dan, Yang Jiangang. Vibration test and data analysis of the decanter centrifuge[J]. Fluid Machinery, 2009(4): 5–8. |
| [14] |
张文.
转子动力学理论基础[M]. 北京: 科学出版社, 1990 Zhang Wen. Rotor dynamics theory basis[M]. Beijing: Science Press, 1990. |
| [15] |
杨建刚.
旋转机械振动分析与工程应用[M]. 北京: 中国电力出版社, 2007 Yang Jiangang. Rotating machinery vibration analysis and engineering applications[M]. Bijing: China Electric Power Press, 2007. |
 2018, Vol. 35
2018, Vol. 35





