固定床技术具有结构简单、操作方便和费用低廉等优点,广泛应用于化学反应、组分分离和提纯等工艺过程。决定固定床技术的性能参数有很多,其中压降对物料流体进入固定床的动量要求及其对床层内的流体流动、传热以及传质过程的影响非常大,准确预测床层压降对于固定床的设计与操作都有十分重要的意义。影响床层压降的因素主要有物料流体本身和固定床结构两方面,前者包括密度、黏度、进料流速等;后者包括填充床层的颗粒形状、粒径、床层空隙率ε、固定床直径D与粒径dp之比D/dp(对应壁面效应)等。
目前研究固定床压降的方法主要有3种:实验研究、理论分析和CFD模拟。其中,实验研究结果是理论分析和CFD模拟的基础,但由于受到模型尺寸、流场扰动和测量精度的限制,实验研究的难度往往非常大,比如当D/dp<15时,显著的壁面效应使实验测量结果的可靠性大大降低;理论分析的优势在于其所得结果往往具有普遍意义,能够清楚地认识各种影响因素,但往往需要对计算对象进行大量的抽象和简化,才可能得到理论解。
在采用理论分析法研究固定床压降方面,Reichelt等[1]和Eisflied等[2]的工作被认为对固定床的设计具有很好的指导意义。前者还基于Ergun半经验公式[3]提出计算固定床压降的经验公式[式(1)~式(4)]。
| $\phi =\frac{{{K}_{1}}A_{\rm{W}}^{2}}{R{{e}_{\rm{d}}}}\frac{{{\left( 1-\varepsilon \right)}^{2}}}{{{\varepsilon }^{3}}}+\frac{{{A}_{\rm{W}}}}{{{B}_{\rm{W}}}}\frac{1-\varepsilon }{{{\varepsilon }^{3}}}$ | (1) |
| ${{A}_{\rm{W}}}=1+\frac{2}{3(D/{{d}_{\rm{p}}})\left( 1-\varepsilon \right)}$ | (2) |
| ${{B}_{\text{W}}}={{\left[ {{k}_{1}}{{\left( \frac{{{d}_{\text{p}}}}{D} \right)}^{2}}+{{k}_{2}} \right]}^{2}}$ | (3) |
| $\phi =\frac{\Delta p}{{{\rho }_{0}}U_{\rm{s}}^{2}}\frac{{{d}_{\rm{p}}}}{L}$ | (4) |
Eisflied等[2]通过对大量实验数据进行拟合,给出了式(1)~式(4)中3个常数项K1、k1和k2的精确值,分别为154、1.15和0.87。对于填充单一粒径的固定床,可直接采用上述半经验公式[式(1)~式(4)]计算床层压降;而对于填充不同粒径的固定床,在采用半经验公式之前需要确定公式中颗粒直径的表达形式,Carman[4]引入了有效直径这一概念,Zeisberger等[5]认为采用数量平均直径(d10)作为有效直径得到的压降预测结果与实验结果更加吻合;Li等[6]指出在高和低两种进料流速下,分别可以采用长度平均直径(d21)和面积平均直径(d32)来替代有效直径;Li等[7]发现采用d32替代不同形状颗粒的有效直径时,计算得到压降值非常接近实验值。
第3种方法,即CFD数值模拟法能够克服实验研究和理论分析2种方法的诸多不足。采用CFD法计算流体流动问题,如同在计算机上进行了相应的物理实验,文献发现通过合理地建模能够准确地再现各种流场细节,获得关于速度场、压力场和湍流场等丰富的重要信息,而采用实验法只能通过一些复杂昂贵的大型仪器才能获得这些信息。很多研究者[8-15]采用实验法和CFD法研究了固定床内的压降,模拟结果与半经验公式或实验结果基本吻合,并基于这些结果对半经验公式进行了改进。
但文献研究的固定床模型的D/dp值一般比较大(D/dp >15),对小D/dp固定床的研究相对要少得多,而且通常假设填充固定床的颗粒为单一粒径分布,而实际固定床中的填充颗粒往往服从特定的粒径分布,如正态分布。鉴于CFD法在研究流体流动以及单相、多相流体系方面的巨大潜力,本研究将采用CFD法分别研究填充单一粒径以及服从不同粒径分布的颗粒的小D/dp固定床内的压降。除此外,考虑到半经验公式对小D/dp固定床适用性较差,提出更为合理的有效直径对公式加以改进。
1 CFD建模 1.1 体系和模型固定床随机填充单一粒径和服从特殊粒径分布的球形颗粒,后者得到的床层为非结构化的,计算量和难度大幅提高。3种粒径分布如表 1所示,d10均为16.5 mm:分布Ⅰ为单一粒径;分布Ⅱ和Ⅲ为正态分布,标准方差分别为0.4和1.0。对应的3种固定床模型编号分别为Ⅰ、Ⅱ和Ⅲ,固定床直径和均为0.1 m(D/dp约为6),床层高度H为0.5 m(H/dp约为30)。
| 颗粒尺寸dp/mm | |||||
| 11.2 | 13.9 | 16.5 | 19.1 | 21.8 | |
| Ⅰ | 0 | 0 | 200.0 | 0 | 0 |
| Ⅱ | 12.0 | 48.0 | 80.0 | 48.0 | 12.0 |
| Ⅲ | 35.0 | 43.0 | 44.0 | 43.0 | 35.0 |
采用基于离散元算法的PFC3D软件实现颗粒的随机堆放。颗粒之间以及颗粒与壁面之间的相互作用采用Hertz接触模型。模拟过程涉及参数主要有剪切模量(sh)为8e10,泊松比(po)为0.33,密度(dens)为3 000 kg/m3,摩擦系数(fric)为0.05,阻尼系数(da)为0.2[16]。为确保物理模型的重复性,所有模型均生成3次。
1.2 网格划分由于计算模型内部结构复杂,采用适应性更强的非结构化网格。Rep较小时,划分边界层以准确捕捉壁面附近的流场细节;而Rep较大时,受网格尺寸的限制,采用“Enhance wall treatment”方法来近似处理壁面附近的流场。网格划分过程具体详细参数见表 2。为确保获得与网格数量无关的模拟结果,层流状态下采用约600万网格,湍流状态下采用约500万网格来划分计算模型。为避免颗粒之间或颗粒与壁面之间互相接触而生成高扭曲度网格,在完成建模后将所有颗粒的粒径均缩减1%。
| 计算模型 | ||
| 湍流模型 | 层流模型 | |
| 四面体网格变长 | 8.5%dp | 8.5%dp |
| 棱形网格层数 | 5 | 0 |
| 第1层棱形网格厚度 | 0.004 | |
| 棱形网格边长增长率 | 0.024%dp | |
模拟过程中选用的物料为空气,黏度μ=1.7894×10-5 Pa·s,密度ρ=1.225 kg·m-3;高湍流状态下选用的湍流模型为standard k-ε模型;所有壁面为无滑移边界条件;进口为速度进口边界条件,进口速度相同,进口与床层之间距离为3dp;出口为压力出口边界条件,出口处压力为101.325 kPa,出口与床层之间距离为7dp。采用SIMPLE算法耦合计算速度场和压力场,当所有控制方程的残差小于10-5认为达到收敛。
2 结果及讨论 2.1 填充单一粒径颗粒固定床 2.1.1 空隙率由200个单一粒径颗粒填充而成的固定床模型Ⅰ,如图 1所示。

|
| 图 1 填充单一粒径固定床模型 Figure 1 Fixed bed model of packed with uniform particles |
| |
PFC3D计算得床层空隙率为0.485,这与Theuerkauf等[16]的研究结果基本吻合。为保证PFC3D软件建立模型的有效性,分析了空隙率沿床层径向的随机振荡变化情况,并与采用De Klerk经验公式(5)~(7)[17]计算结果进行了比较,如图 2所示。
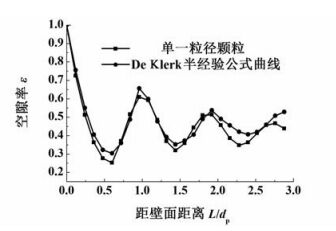
|
| 图 2 2种空隙率分布曲线比较 Figure 2 Comparison of two radial profiles for void fraction |
| |
通过计算平行于固定床轴线的不同直径环隙间的床层空隙确定空隙率的径向分布[18]。
| $z\text{=}\frac{R-r}{d}$ | (5) |
当z≤0.637时,
| $\varepsilon \left( r \right)=2.14{{z}^{2}}-2.53z+1$ | (6) |
当z>0.637时,
| $\begin{array}{l} \varepsilon \left( r \right) = 0.29{\rm{exp}}\left( { - 0.6z} \right)[{\rm{cos}}(2.3{\rm{\pi }}\left( {z - 0.16} \right))]\\ \quad \quad \quad \quad \quad + 0.15{\rm{exp}}\left( { - 0.9z} \right) + {\varepsilon _{\rm{b}}} \end{array}$ | (7) |
从图 2可以看到PFC3D软件生成的填充模型的空隙率分布与de Klerk经验公式[17]得到的空隙率分布基本一致,均呈现为衰减的正弦波。在靠近壁面处,二者几乎完全相同,在床层中心处,二者略有不同,同时说明采用PFC3D软件建立的固定床模型合理有效,可以用于CFD模拟研究。
2.1.2 压力分布采用CFD模拟研究固定床,除了要求建模结构合理以外,还要求模型能够代表整个床层。图 3展示了低进料速度下固定床内的压力分布情况。
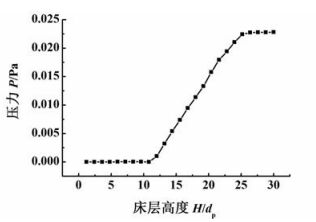
|
| 图 3 床层内压力分布 Figure 3 Pressure distribution in the fixed bed |
| |
从图 3中可以清楚地看到在床层上下两端附近压力几乎保持不变,而在床层内部压力呈线性变化,这说明物料进口和出口距床层的距离已经足够长,可以忽略进口和出口效应对于固定床内压力场的影响,同时说明由200个颗粒组成的固定床模型足以代表整个床层,能够体现床层压力的整体变化。
2.1.3 床层压降将固定床进出口压力差,即压降ΔP的模拟结果与半经验公式计算结果进行比较,如图 4所示。
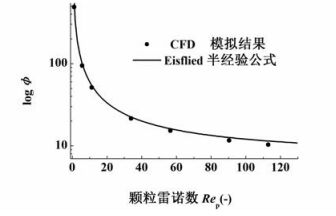
|
| 图 4 Rep<120时压降的CFD结果与半经验公式结果之间的比较 Figure 4 Comparison of pressure drop results between CFD and semi-empirical equation at Rep < 120 |
| |
在低雷诺数(Rep<120)时,CFD模拟结果与Eisflied半经验公式结果之间的相对误差较小(<10%)。但随着Rep的增大,二者之间的相对误差有所增大(<25%),并呈现先减小后增大的趋势(见图 5)。这说明CFD模拟结果与Eisflied半经验公式均能够合理地预测单一粒径固定床床层压降。

|
| 图 5 Rep >120时压降的CFD结果与半经验公式结果之间的相对误差 Figure 5 The relative error of pressure drop results between CFD and semi-empirical equation at Rep>120 |
| |
采用上述方法建立填充不同粒径颗粒的固定床模型,如图 6所示。由于大颗粒之间的缝隙能够由小颗粒进行填补,所以固定床模型Ⅱ和Ⅲ的总体空隙率相对较小,分别为0.464和0.450。

|
| 图 6 填充不同粒径颗粒固定床模型 Figure 6 Fixed bed model packed with different particles |
| |
图 7为3种固定床模型的空隙率的径向分布,3者均呈震荡衰减的趋势。除此外,模型Ⅱ和Ⅲ的峰位置向床层中心偏移,粒径分布标准差越大,该现象越明显。由于靠近固定床壁面的颗粒受壁面限制而规整排列一侧,这使得壁面附近空隙率分布较为规律,即空隙率在离壁面1/2粒径位置处出现最小值,而1个粒径位置处达到峰值。
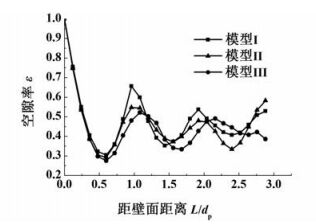
|
| 图 7 不同颗粒分布堆积模型中空隙率分布对比 Figure 7 Comparison of void fraction profiles in different fixed bed models |
| |
从图 7还可以看出靠近壁面处空隙率的第1个峰值位置与壁面之间的距离和颗粒的质量平均直径(d43)相当,这说明填充颗粒的有效直径与d43相近。同时为确保模型结果与颗粒堆放位置无关,3种固定床模型均随机生成3次,模拟结果与上述结果基本一致。
2.2.2 粒径对床层压降的影响固定床内空隙率分布会影响流体流动,从而影响床层压降。在低雷诺数(Rep<120)分别对固定床模型Ⅱ和Ⅲ内压降的CFD模拟结果和Eisflied半经验公式计算结果进行了比较,如图 8所示。

|
| 图 8 Rep<120时压降CFD结果与采用不同平均粒径的半经验公式计算结果之间的比较 Figure 8 Comparisons of pressure drop results between CFD and empirical equations using different mean diameters at Rep < 120 |
| |
由于固定床内颗粒粒径不同,需要选择1个适当的平均粒径(如d10、d21、d32和d43)来替代原半经验公式中的粒径参数。从图 8中可以看出将d43作为平均粒径代入半经验公式得到的计算结果与模拟结果之间的偏差最小(<9%),说明采用d43替代半经验公式中的粒径最为合理。固定床结构是决定其床层压降的一个关键因素,而对于小D/dp固定床而言,大粒径的颗粒对固定床结构的影响较为显著,因此选用尽量体现大粒径颗粒作用的平均粒径来估算床层压降能够得到更为准确的计算结果。该结论与文献结论存在差异,原因可能是本研究的固定床的D/dp较小,大粒径颗粒足以影响整个床层结构,而对于D/dp较大的固定床,床层中部颗粒的排布受壁面影响较小,处于随机混乱的堆积状态,此时颗粒粒径的大小对其结构影响并不显著。
高雷诺数(Rep>200)下2种固定床模型内的压降模拟结果与半经验公式计算结果之间的相对误差如图 9所示。
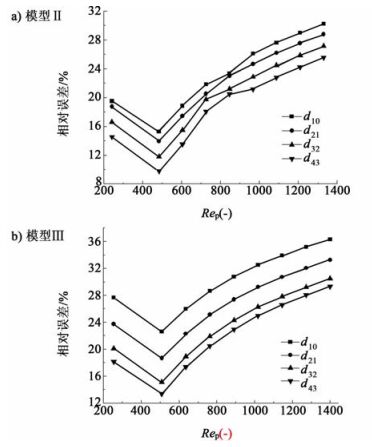
|
| 图 9 Rep>200时压降CFD结果与采用不同平均粒径的半经验公式计算结果之间相对误差的比较 Figure 9 Comparisons of relative error of pressure drop results between CFD and empirical equations using different mean diameters at Rep>200 |
| |
所有相对误差值普遍较大(>10%),造成该现象的主要原因是湍流模型[19]和计算网格。当半经验公式采用d43粒径时,相对误差最小。随着Rep的增大,相对误差均呈先减小后增大的趋势,和图 5基本一致。原因可能是当Rep较小时,固定床内的流体部分处于过渡状态,此时采用湍流模型来计算压降误差较大;而随着Rep的增大,流体逐渐处于湍流状态,此时采用湍流模型模拟压降所得结果与半经验公式计算结果之间的误差逐渐减小;但随着流体速度的进一步增大,相对误差继续增大。
比较图 5和图 9也可以看出,随着填充颗粒粒径不均匀度的增大,在相同的Rep下,模拟结果与半经验公式计算结果之间的相对误差增大,造成这种现象的主要原因是:随着填充颗粒不均匀度的增大,床层内部结构变得更加复杂,流体流过的通道变得更加扭曲,此时采用各向同性的standard k-ε模型湍流模型和原有的计算网格来计算床层压降使相对误差增大。
3 结论采用CFD法研究小D/dp的固定床内的压降,基于standard k-ε模型、SIMPLE算法、边界层等方法和模型进行模拟计算,得到的结论主要有:
对于单一粒径颗粒填充的固定床,在低雷诺数即Rep小于120左右时,CFD法和半经验公式能够预测到相似的压降值,而在高雷诺数下二者之间的相对误差有所增大,并呈现先减小后增大的趋势
对于填充不同粒径颗粒的固定床,选用d43粒径作为有效粒径,能够更好解释床层空隙率的分布形式。同时,采用d43替代原半经验公式的粒径参数得到的压降值与模拟结果最为接近,对于小D/dp固定床选用d43作为有效直径能够提高半经验公式的预测准确度。
| [1] | Reichelt W. Zur Berechnung des Druchverlustes einphasig durchströmter kugelund Zylinderschüttugen[J]. Chem Ing Tech, 1972, 23: 342–361. |
| [2] | Eisfeld B, Schnitzlein K. The influence of confining walls on the pressure drop in packed beds[J]. Chemical Engineering Science, 2001, 56: 4321–4329. DOI: 10.1016/S0009-2509(00)00533-9 |
| [3] | Ergun S. Fluid flow through packed columns[J]. Chem Eng Prog, 1952, 48(2): 89–94. |
| [4] | Carman P C. Fluid flow through granular beds[J]. Transactions of the Institution of Chemical Engineers, 1937, 15: 150–166. |
| [5] | Zeisberger A, Mayinger F. Heat transport and void fraction in granulated debris[J]. Nuclear Engineering and Design, 2006, 236: 2117–2123. DOI: 10.1016/j.nucengdes.2006.03.025 |
| [6] | Li L, Ma W. Experimental characterrization of the effective particle diameter of a particulate bed packed with multi-diameter spheres[J]. Nuclear Engineering and Design, 2011, 241: 1736–1745. DOI: 10.1016/j.nucengdes.2011.03.013 |
| [7] | Li L, Ma W. Experimental study on the effective particle diameter of a packed bed with non-spherical particles[J]. Transp Porous Med, 2011, 89: 35–48. DOI: 10.1007/s11242-011-9757-2 |
| [8] | Dalman M T, Merkin J H, Mcgreavy C. Fluid flow and heat transfer past two spheres in a cylindrical tube[J]. Computers & Fluids, 1986, 14: 267–281. |
| [9] | Calis H P A, Nijenhuis J, Paikert B C, et al. CFD modeling and experimental validation of pressure drop and flow profile in a novel structured catalytic reactor packing[J]. Chemical Engineering Science, 2001, 56: 1713–1720. DOI: 10.1016/S0009-2509(00)00400-0 |
| [10] | Reddy R K, Joshi J B. CFD modeling of pressure drop and drag coefficient in fixed and expended beds[J]. Chemical Engineering Research and Design, 2008, 86: 444–453. DOI: 10.1016/j.cherd.2007.12.007 |
| [11] | Atmakidis T, Kenig E Y. CFD-Based analysis of the wall effect on the pressure in packed beds with moderate tube/particle diameter ratios in the laminar flow regime[J]. Chemical Engineering Journal, 2009, 155: 404–410. DOI: 10.1016/j.cej.2009.07.057 |
| [12] | Maker M J, Tabor G R. Computational analysis of transitional air flow through packed columns of spheres using the finite volume technique[J]. Computers and Chemical Engineering, 2010, 34: 878–885. DOI: 10.1016/j.compchemeng.2009.10.013 |
| [13] | Reddy R K, Joshi J B. CFD modeling of pressure drop and drag coefficient in fixed beds:Wall effects[J]. Particuology, 2010, 8: 37–43. DOI: 10.1016/j.partic.2009.04.010 |
| [14] | Eppinger T, Seidler K, Kraume M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios[J]. Chemical Engineering Journal, 2011, 166: 324–331. DOI: 10.1016/j.cej.2010.10.053 |
| [15] | Augier F, Idoux F, Delenne J Y. Numerical simulations of transfer and transport properties inside packed beds of spherical particles[J]. Chemical Engineering Science, 2010, 65: 1055–1064. DOI: 10.1016/j.ces.2009.09.059 |
| [16] | Theuerkauf J, Witt P, Schwesig D. Analysis of particle porosity distribution in fixed beds using the discrete element method[J]. Powder Technology, 2006, 165: 92–99. DOI: 10.1016/j.powtec.2006.03.022 |
| [17] | DeKlerk A. Voidage variation in packed beds at small column to particle diameter ratio[J]. AIChE J, 2003, 49: 2022–2029. |
| [18] | DuToit C G. The numerical determination of the variation in the porosity of the pebble-bed core[J]. In:Proceedings of 1st international topical meeting on high temperature reactor technology (HTR2002), 2002. |
| [19] | Guardo A, Coussirat M, Larrayoz M A, et al. Influence of the turbulence model in CFD modeling of wall-to-fluid heat transfer in packed beds[J]. Chemical Engineering Science, 2005, 60: 1733–1742. DOI: 10.1016/j.ces.2004.10.034 |
 2017, Vol. 34
2017, Vol. 34





