茚在工业上是一种非常重要的原料,主要用于制造茚-古马隆树脂以及苯乙烯-茚树脂[1],高纯度的茚是一种非常重要的共聚物,广泛用于改变分子的表面活性[2]。在生物以及医药领域,茚可以用作药物中间体[3-4]。茚主要来源于煤焦油中的一个含茚的馏分里[5],将这个馏分中的茚初步提纯后会含有一些杂质,而杂质中最难以去除的则是苯甲腈。汽液平衡数据是设计精馏流程的基础,而苯甲腈与茚二元体系的汽液平衡数据在已知文献中还没有,所以测量苯甲腈与茚的汽液平衡数据是很有意义的。
茚在常压下的沸点是454.75 K,在这个温度下,茚容易发生自聚,通过降低实验压力来降低实验温度。本研究测量了这个二元体系分别在22.0、32.0和42.0 kPa下的汽液平衡数据,并应用了Wilson方程[6]、NRTL方程[7]以及UNIQUAC方程[8]来拟合实验数据,结果显示这3种状态方程都能很好地拟合实验数据,运用了Herington[9]以及van Ness 2种方法来对实验数据进行热力学一致性检验,结果可以很好地通过检验。
1 实验部分 1.1 实验药品实验所用的药品均未经过进一步的提纯,其中,苯甲腈来自于TCI,其质量分数为0.997;茚来自于Aladdin,其质量分数为0.990。药品的纯度用气相色谱仪(GC-7 890 A, Agilent Technologies)来测定以及标定。表 1以及表 2是所用药品的一些基础物理性质以及安托尼常数。
| Component | Benzonitrile | Indene | |
| Antoine | |||
| constants | A | 6.795 06 | 6.344 100 |
| B | 2 066.710 | 1 749.215 | |
| C | -32.190 | -52.375 | |
| Temperature range/K | 301.4~463.8 | 289.6~454.8 | |
| a Antoine equation: log10P=A-B/(T+C),其中P/kPa, T/K。 | |||
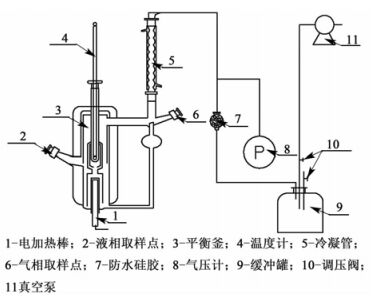
图 1为实验装置的简图。平衡釜的总容量约为140 mL,其中加样量约为50 mL,从液相取样口加入药品,然后通过热电偶来控制电加热棒给平衡釜加热。汽相在冷凝管冷凝后一小部分储存于汽相取样口,然后通过汽相取样口回流到平衡釜中,这种测量汽液平衡数据的方法叫做汽相冷凝循环法,可以有效地降低平衡釜内的过热情况。系统通过1个SHB-B95型真空泵来提供压力条件,并通过2个调压阀来控制压力。真空泵连续运行,使得体系内的压力可以在很长的时间内保持稳定。当体系温度在60 min内不再发生变化,则可以认为体系达到了汽液平衡状态。然后通过汽相和液相取样口各取出约1 mL的样品,通过气相色谱仪(GC-7890 A, Agilent Technologies)来测定样品的浓度。气相色谱仪在实验前使用精密天平(精确到0.0001 g)量取的标准试样进行了标定。每份样品至少分析3次,直到3次所测得的摩尔分数之间的差距少于0.5%。体系温度由1个插入平衡釜中但并不与体系接触的精密水银温度计测量,其测量精度为±0.05 K。体系压力由1个经过水银柱标定的精密压力表测量,其精度为±0.04 kPa,量程为0~100 kPa。
|
| 图 1 装置简图 Figure 1 Schematic diagram of the VLE apparatus |
| |
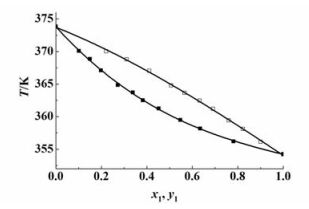
实验前,通过测量正丙醇与正丁醇体系在53.3 kPa下的汽液平衡数据并与已知文献[15]中的数据进行对比来验证装置的可靠性。结果如图 2所示。
图 2中,2条曲线分别代表文献数据汽相组成和液相组成,实心点为实验数据的液相组成点,空心点为汽相组成点。从图 2中可以看出,实验数据点基本都分布在文献数据拟合的曲线两端,所以用上述装置所测得的实验数据与文献数据吻合得很好,说明实验装置的可靠性很好。
2 实验结果及讨论 2.1 实验数据22.0、32.0和42.0 kPa下的苯甲腈与茚二元体系的等压汽液平衡实验数据如表 3所示。
| x1exp | y1exp | Texp | γ1exp | γ2exp |
| P=22.0 kPa | ||||
| 1.0000 | 1.0000 | 411.20 | 1.0000 | |
| 0.9328 | 0.8901 | 410.03 | 0.9927 | 1.2669 |
| 0.8571 | 0.7902 | 408.77 | 1.0004 | 1.1835 |
| 0.7843 | 0.6985 | 407.77 | 0.9995 | 1.1632 |
| 0.7159 | 0.6198 | 406.76 | 1.0053 | 1.1502 |
| 0.6407 | 0.5447 | 406.04 | 1.0117 | 1.1146 |
| 0.5615 | 0.4729 | 405.03 | 1.0374 | 1.0924 |
| 0.3668 | 0.3076 | 403.41 | 1.0921 | 1.0475 |
| 0.2482 | 0.2091 | 402.75 | 1.1225 | 1.0298 |
| 0.1307 | 0.1162 | 402.37 | 1.2003 | 1.0077 |
| 0.0853 | 0.0782 | 402.24 | 1.2433 | 1.0032 |
| 0.0556 | 0.0533 | 402.19 | 1.3023 | 0.9995 |
| 0.0376 | 0.0370 | 402.16 | 1.3382 | 0.9987 |
| 0.0000 | 0.0000 | 402.13 | 1.0000 | |
| P=32.0 kPa | ||||
| 1.0000 | 1.0000 | 422.78 | 1.0000 | |
| 0.9114 | 0.8695 | 421.46 | 0.9973 | 1.1710 |
| 0.8345 | 0.7711 | 420.14 | 1.0070 | 1.1435 |
| 0.7526 | 0.6724 | 419.20 | 1.0031 | 1.1260 |
| 0.6946 | 0.6045 | 418.30 | 1.0055 | 1.1313 |
| 0.6214 | 0.5244 | 417.43 | 1.0026 | 1.1266 |
| 0.5111 | 0.4252 | 416.28 | 1.0256 | 1.0918 |
| 0.4148 | 0.3475 | 415.66 | 1.0537 | 1.0552 |
| 0.3067 | 0.2601 | 415.00 | 1.0897 | 1.0305 |
| 0.2114 | 0.1817 | 414.46 | 1.1240 | 1.0187 |
| 0.1373 | 0.1209 | 414.13 | 1.1639 | 1.0106 |
| 0.0737 | 0.0687 | 413.98 | 1.2382 | 1.0017 |
| 0.0401 | 0.0389 | 413.91 | 1.2915 | 0.9998 |
| 0.0000 | 0.0000 | 413.88 | 1.0000 | |
| P=42.0 kPa | ||||
| 1.0000 | 1.0000 | 431.73 | 1.0000 | |
| 0.9202 | 0.8809 | 430.40 | 0.9982 | 1.2031 |
| 0.8074 | 0.7278 | 428.63 | 0.9915 | 1.1978 |
| 0.6943 | 0.6051 | 427.28 | 0.9987 | 1.1379 |
| 0.6212 | 0.5233 | 426.34 | 0.9935 | 1.1389 |
| 0.5221 | 0.4357 | 425.43 | 1.0121 | 1.0970 |
| 0.4495 | 0.3812 | 424.72 | 1.0513 | 1.0660 |
| 0.3607 | 0.3082 | 424.17 | 1.0774 | 1.0428 |
| 0.2562 | 0.2217 | 423.50 | 1.1140 | 1.0283 |
| 0.1877 | 0.1661 | 423.30 | 1.1463 | 1.0148 |
| 0.1263 | 0.1152 | 423.11 | 1.1886 | 1.0066 |
| 0.0692 | 0.0663 | 422.98 | 1.2535 | 1.0009 |
| 0.0386 | 0.0384 | 422.92 | 1.3040 | 0.9998 |
| 0.0000 | 0.0000 | 422.88 | 1.0000 | |
| a:u(T)=±0.05 K,u(x)=0.001。 | ||||
为了验证实验数据的可靠性,应用了Herington面积法,van Ness微分法2种方法来对实验数据进行热力学一致性检验。
对于面积法
| $D = 100\frac{{\left| {\int_{x{_1} = 0}^{x{_1} = 1} {{\rm{ln}}\frac{{{\gamma _1}}}{{{\gamma _2}}}{\rm{d}}{x_1}} } \right|}}{{\left| {\int_{x{_1} = 0}^{x{_1} = 1} {{\rm{ln}}\left| {\frac{{{\gamma _1}}}{{{\gamma _2}}}} \right|{\rm{d}}{x_1}} } \right|}}$ | (1) |
| $J = 150\frac{{{T_{{\rm{max}}}} - {T_{{\rm{min}}}}}}{{{T_{{\rm{min}}}}}}$ | (2) |
其中,Tmax和Tmin分别表示测量体系的最高沸点和最低沸点。Herington认为,如果(D-J)的值小于10,则可以认为实验数据是符合热力学一致性的。苯甲腈与茚在22.0、32.0、42.0 kPa下的面积法热力学一致性检验结果如表 4所示。
| P/ kPa | D | J | D-J |
| 22.0 | 12.39 | 3.12 | 9.27 |
| 32.0 | 4.35 | 2.93 | 1.42 |
| 42.0 | 8.33 | 2.90 | 5.43 |
结果显示在这3个压力下的实验数据都能通过面积法检验。Wisniak(1994)[16]验证过面积法不能肯定一组实验数据的热力学一致性,也就是说,通过面积法检验的实验数据有可能是不准确的,然而面积法还是广泛的应用于热力学一致性检验。
对于van Ness检验法,用1个4参数的Legendre多项式来表示超额吉布斯自由能。
| $g = \frac{{{G^E}}}{{RT}} = {x_1}(1 - {x_1})\sum\limits_{}^k {{a_k}} {L_k}({x_1})$ | (3) |
其中k取值为4。对下列目标函数进行优化,
| $F = \sum ({y_{{\rm{1cal}}}} + {y_{{\rm{2cal}}}} - 1)$ | (4) |
使得F最小,其中,y1 cal表示计算得到的苯甲腈的气相摩尔分数,y2 cal表示计算得到的茚的气相摩尔分数。
Gmehling和Onken认为当气相摩尔分数的平均偏差Δy小于0.01的时候,可以认为实验数据是通过热力学一致性检验的。而计算得到的22.0、32.0和42.0 kPa 3个压力下的Δy分别为0.003、0.004和0.006,均小于0.01。所以所得到的实验数据能通过van Ness的微分法热力学一致性检验。
2.3 数据拟合在低压的条件下,气体的状态可以当成理想气体来处理,于是,物质的活度系数可以通过式(5)来计算。
| ${\gamma _i} = \frac{{{y_i}P}}{{{x_i}P_i^s}}$ | (5) |
式(5)中,Pis是纯物质i在平衡温度下的饱和蒸汽压。Pis的值可以通过安东尼方程来计算。
| ${\rm{lo}}{{\rm{g}}_{10}}P = A - \frac{B}{{T + C}}$ | (6) |
活度系数则可以通过式(7)来计算物质的超额吉布斯自由能。
| ${G^E} = RT({x_1}{\rm{ln}}{\gamma _1} + {x_2}{\rm{ln}}{\gamma _2})$ | (7) |
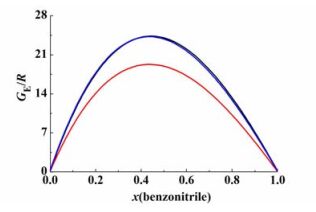
图 3是苯甲腈与茚二元体系在22.0、32.0、42.0 kPa 3个压力下超额吉布斯自由能和组成的关系图。
|
| 图 3 超额吉布斯自由能与组成关系图 Figure 3 Calculated excess Gibbs energy versus mole fraction |
| |
图 3中,黑线、红线和蓝线分别代表 22.0、32.0和42.0 kPa下的超额吉布斯自由能。
用随机选取的大部分实验数据来进行NRTL,Wilson以及UNIQUAC方程的数据拟合,而另一小部分实验数据则拿来和拟合的数据进行对比,结果如图 4所示。

|
| 图 4 苯甲腈与茚的T-x-y图 Figure 4 T-x-y diagram for the benzonitrile (1)+indene (2) system |
| |
图 4中,黑线表示一部分实验数据用NRTL方程拟合得到的曲线,空心黑点表示用来拟合曲线的实验数据点,实心黑点表示用来与拟合曲线比较的实验数据点。从上至下依次为22.0、32.0和42.0 kPa下的T-x-y图。从图 4可知,实验数据都分布在拟合曲线的两边。
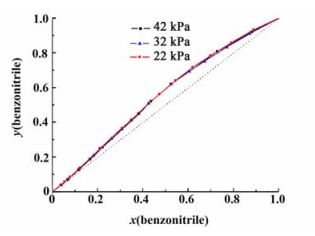
图 5是苯甲腈与茚在22.0、32.0和42.0 kPa下的y-x图。图 5中,红色、蓝色和黑色的点分别代表 22.0、32.0和42.0 kPa下测得的实验数据点,红线,蓝线,黑线分别代表实验数据拟合得到的曲线。
|
| 图 5 苯甲腈与茚的y-x图 Figure 5 y-x diagram for the benzonitrile (1)+indene (2) system |
| |
从T-x-y图与y-x图可以看出,当两物质组成接近纯茚时,泡点线与露点线在纯茚的一端接近于相切。这种非理想性使得要通过普通的精馏方法得到纯茚变得很困难。
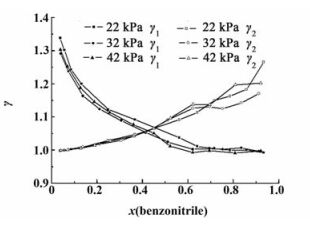
各个压力下通过实验得到的活度系数与组成的关系如图 6所示。
|
| 图 6 活度系数与组成图 Figure 6 Activity coefficient and composition |
| |
实验数据应用Wilson方程、NRTL方程以及UNIQUAC方程来拟合,通过最优化求解下列目标函数F[17]的最小值,
| $F = {\sum\limits_{k = 1}^n {\sum\limits_{i = 1}^2 {\left( {\frac{{\gamma _i^{{\rm{exp}}} - \gamma _i^{{\rm{cal}}}}}{{\gamma _i^{{\rm{exp}}}}}} \right)} } ^2}$ | (8) |
可以得到用各方程拟合的活度系数,进而可以求解各方程对应的二元交互作用参数参数。式(8)中,n是实验数据点个数,NRTL方程中的α值设定为0.3。用Wilson方程、NRTL方程以及UNIQUAC方程计算得到的二元交互作用参数以及关于气相摩尔分数与泡点温度的计算值与实验值之间的均方根偏差如表 5所示。
| Benzonitrile+Indene | |||||
| model | A12a/K | A21a/K | α | σTb/K | σyb |
| P=22.0 kPa | |||||
| NRTL | -112.08 | 241.19 | 0.3 | 0.099 | 0.0026 |
| Wilson | 0.63 | 1.16 | 0.110 | 0.0028 | |
| UNIQUAC | -118.04 | 173.08 | 0.107 | 0.0028 | |
| P=32.0 kPa | |||||
| NRTL | -231.92 | 392.84 | 0.3 | 0.092 | 0.0038 |
| Wilson | 0.54 | 1.37 | 0.220 | 0.0058 | |
| UNIQUAC | -162.92 | 229.17 | 0.225 | 0.0056 | |
| P=42.0 kPa | |||||
| NRTL | -197.92 | 352.15 | 0.3 | 0.054 | 0.0060 |
| Wilson | 0.53 | 1.33 | 0.055 | 0.0069 | |
| UNIQUAC | -158.26 | 229.35 | 0.060 | 0.0067 | |
| a 3个模型的二元相互作用参数表达式: | |||||
| Wilson, Aij=(λij-λii)/R; NRTL, Aij=(gij-gii)/R; UNIQUAC, Aij=(Uij-Uii)/R。 | |||||
| | |||||
从表 5中可以看到,用拟合得到的二元交互作用参数计算得到的气相摩尔分数与泡点温度,它们的均方根偏差分别小于0.006 9及0.225 K。并且用3种方程计算得到的数据偏差很小,由此可见,3种模型都能用于计算苯甲腈与茚二元体系的等压汽液平衡数据。
3 结论应用汽相冷凝循环法测定了苯甲腈与茚二元体系在22.0、32.0和42.0 kPa下的汽液平衡数据,并应用面积检验法和微分检验法2种方法对所测实验数据进行了热力学一致性检验,结果显示所测数据都能通过热力学一致性检验。应用了Wilson模型、NRTL模型以及UNIQUAC模型来对实验数据进行拟合,得到了3种模型下此体系的二元交互作用参数,结果显示实验数据能与拟合数据较好地吻合。
| [1] | 张国锋. 焦化重油精制[D]. 北京: 北京化工大学, 2010. Zhang Guofeng. Purification of coking heavy oil[D]. Beijing:Beijing University of Chemical Technology, 2010(in Chinese) http://cdmd.cnki.com.cn/article/cdmd-10010-2010170623.htm |
| [2] | Brzozowska T, Zielinski J, Machnikowski J. Effect of polymeric additives to coal tar pitch on carbonization behaviour and optical texture of resultant cokes[J]. Journal of Analytical and Applied Pyrolysis, 1998, 48(1): 45–58. DOI: 10.1016/S0165-2370(98)00101-6 |
| [3] | Buckland B C, Drew S W, Connors N C, et al. Microbial conversion of indene to indandiol:A key intermediate in the synthesis of CRIXIVAN[J]. Metabolic Engineering, 1999, 1(1): 63–74. DOI: 10.1006/mben.1998.0107 |
| [4] | Lu M, Mulholland J A. Aromatic hydrocarbon growth from indene[J]. Chemosphere, 2001, 42(5): 625–633. |
| [5] | Hiroaki M, Youko S. Production process of indene:US, 6818121[P]. 2004-11-16 |
| [6] | Wilson G M. Vapor-Liquid equilibrium. X I. A new expression for the excess free energy of mixing[J]. Journal of the American Chemical Society, 1964, 86(2): 127–130. DOI: 10.1021/ja01056a002 |
| [7] | Renon H, Prausnitz J M. Local compositions in thermodynamic excess functions for liquid mixtures[J]. AIChE Journal, 1968, 14(1): 135–144. |
| [8] | Abrams D S, Prausnitz J M. Statistical thermodynamics of liquid mixtures:A new expression for the excess Gibbs energy of partly or completely miscible systems[J]. AIChE Journal, 1975, 21(1): 116–128. |
| [9] | Herington E F G. Tests for the consistency of experimental isobaric vapor-liquid equilibrium data[J]. J Inst Petrol, 1951, 37: 457–470. |
| [10] | 程能林. 溶剂手册[M]. 第4版. 北京: 化学工业出版社, 2008 |
| [11] | David R L. CRC handbook of chemistry and physics[M]. 87th ed. Taylor and Francis: Boca Raton, FL, 2007. |
| [12] | Horstmann S, Gardeler H, Bölts R, et al. Vapor-Liquid equilibria and excess enthalpy data for the binary systems benzene+benzonitrile and toluene+ benzonitrile covering the temperature range from 323.15 to 413.15 K[J]. Journal of Chemical & Engineering Data, 1999, 44(3): 539–543. |
| [13] | Poling B E, Prausnitz J M, John P O C, et al. The properties of gases and liquids[M]. New York: McGraw-Hill, 2001. |
| [14] | 马沛生, 李永红. 化工热力学[M]. 第2版. 北京: 化学工业出版社, 2010 |
| [15] | Mohsen-Nia M, Memarzadeh M R. Isobaric (vapour+ liquid) equilibria for the (1-propanol+1-butanol) binary mixture at (53.3 and 91.3) kPa[J]. The Journal of Chemical Thermodynamics, 2010, 42(6): 792–796. DOI: 10.1016/j.jct.2010.02.001 |
| [16] | Wisniak J. The Herington test for thermodynamic consistency[J]. Industrial & Engineering Chemistry Research, 1994, 33(1): 177–180. |
| [17] | 高光华. 化工热力学[M]. 第2版. 北京: 清华大学出版社, 2000 |
 2017, Vol. 34
2017, Vol. 34