降低操作温度是固体氧化物燃料电池的发展趋势,其面临的主要问题是寻找在较低温度下离子导电性能良好的电解质。掺杂氧化铈(DCO)因在中低温范围内具有较高的氧离子电导率而受到了广泛关注。但是在还原气氛中,Ce4+的还原带来的电子电导限制了其应用[1-2]。在DCO主相中引入第二相,形成两相复合电解质材料,可以有效的抑制单相DCO在低氧气氛下的电子电导。目前已研究过的体系有DCO-硫酸盐[3],DCO-卤化物[4],DCO-碳酸盐[4-5]等,其中最典型的是DCO-碳酸盐复合体系。DCO-碳酸盐复合电解质不仅在400~600 ℃范围内具有较高的离子电导率,而且在燃料电池操作条件下存在氧离子和质子的共同传导[6-7]。
关于DCO-碳酸盐复合电解质导电性能的研究已经有很多,但是关于H+和O2-在DCO-碳酸盐复合电解质中的传导机制的研究还比较缺乏。对于氧离子的传导,较普遍的观点是氧离子主要通过DCO体相和复合电解质的两相界面进行传导,而且氧离子更易于在两相界面处迁移[8-11]。Zhu等[9]认为氧空位在两相界面区域的浓度远高于在陶瓷相体相中的浓度,同时界面区域的电荷效应降低了O2-迁移的活化能,因此促进了O2-的传导。依据这一观点,可以解释Liu等[11]报道的复合电解质的氧离子电导率随碳酸盐含量先增加后减小的现象。但是,尚无直接的证据可以证明两相界面对氧离子传导的促进作用。与此不同,Zhao等[12-13]指出氧离子不仅能通过DCO体相进行传导,而且能在熔融碳酸盐中迁移,并用直流四电极法测得了熔融碳酸盐的氧离子电导率。Yin等[14-15]的实验结果也表明熔融碳酸盐具有较高的氧离子电导率,并以Na2CO3-K2CO3为电解质用电化学的方法分解Fe2O3制得了Fe和O2。
对于质子的传导,一种较普遍的观点是质子通过两相界面进行传导[8, 16]。2011年Wang等[16]针对钐掺杂氧化铈(SDC)-碳酸钠复合电解质中的超离子导电性提出的“Swing Model”认为:两相界面处形成的Ce—O—H—O—CO22-键合作用为H+的传导提供了快速通道,熔融碳酸盐的存在对于这种效应至关重要。另一种较为被认可的观点是H+可以通过与CO32-结合生成HCO3-,在碳酸盐体相内传导[17]。但是,Liu等[18]以Ce0.8M0.2O2-δ(M=La, Y, Gd, Sm)为电解质成功实现了电化学氨合成,直接证明了Ce0.8M0.2O2-δ(M=La, Y, Gd, Sm)的质子导电性。Sun等[19]也用“氢渗透测试”的方法证明SDC具有一定的质子导电性。
本研究中,我们依据O2-和H+均能通过DCO和熔融碳酸盐体相进行传导的事实,利用随机电阻网络模型(RRN)对DCO-碳酸盐复合电解质的O2-电导率和H+电导率进行了计算,研究了碳酸盐体积分数、DCO颗粒的粒径大小、温度对复合电解质电导率的影响,并与文献报道的实验数据进行了对比。
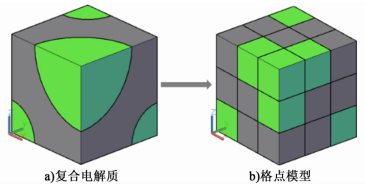
1 计算方法 1.1 电阻网络的生成本研究用两相随机格点模型来模拟DCO-碳酸盐复合电解质(如图 1所示)。若复合电解质取样空间尺度为L,每个格点的尺度为l,则模型中含有ND个格点(N=L/l,D为空间维数)。
|
| 图 1 用三维格点模型近似复合电解质相结构 Figure 1 Using a 3D lattice to approximate the structure of the composite electrolyte |
| |
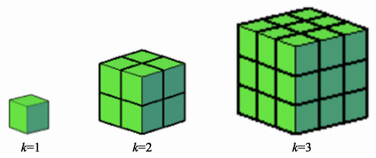
我们以1个格点表示1个碳酸盐颗粒。为了研究DCO颗粒大小对复合电解质导电性能的影响,我们引入DCO与碳酸盐颗粒的粒径比k来表示DCO颗粒相对于碳酸盐颗粒的大小。k=1、2和3时,每个DCO颗粒的大小如图 2所示,即每个DCO颗粒用k3个格点组成的大立方体表示。
|
| 图 2 DCO颗粒大小示意图 Figure 2 Particle-size of DCO |
| |
在给定碳酸盐体积分数XCar和k的条件下,格点模型生成过程如下:1) 建立1个大小为N×N×N的格点模型,初始时所有格点均为碳酸盐相格点。我们用1个大小为N×N×N的三维矩阵A对格点模型进行标记,矩阵中的每个元素对应1个格点。矩阵A中包含2种元素,值为‘1’的元素对应的格点表示DCO相,值为‘1’的元素对应的格点表示碳酸盐相。初始时A中所有元素的值均为‘1’。2) 在格点模型中随机选取1个位点i,尝试在该位置处放入1个DCO颗粒。若A中与新放入DCO颗粒对应位置处的元素值均为‘1’,即新放入的DCO颗粒不与已放入的DCO颗粒冲突,则放入成功,并将A中相应位置处的元素值设为‘0’;否则继续选取下1个随机位点。3) 重复2),直至碳酸盐体积分数达到设定值。
所得格点模型中碳酸盐相的体积分数为:
| $ {X_{{\rm{Car}}}} = \frac{{\sum\nolimits_1^{{N^3}} {A\left( i \right)} }}{{{N^3}}} $ | (1) |
若DCO相和碳酸盐相的电导率分别为σDCO和σCar,则每个DCO相和每个碳酸盐相格点的电导分别为:
| $ {g_{{\rm{DCO}}}} = {\sigma _{{\rm{DCO}}}}\frac{s}{l} = {\sigma _{{\rm{DCO}}}}l $ | (2) |
| $ {g_{{\rm{Car}}}} = {\sigma _{{\rm{Car}}}}\frac{s}{l} = {\sigma _{{\rm{Car}}}}l $ | (3) |
其中s=l2,表示每个格点垂直于坐标轴的截面积。
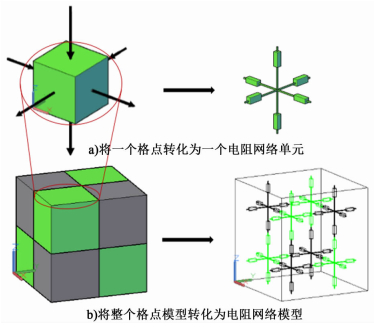
假设只有面接触的相邻格点间能进行电传导,而点接触和棱接触的相邻格点间不能进行电传导,即离子只沿着垂直于格点表面的方向进行传导[如图 3a)左图所示],那么就可以将1个格点看成是1个由6个小电阻通过1个节点连接起来的电阻网络单元[如图 3a)所示],每个小电阻的阻值均为整个格点电阻的一半。如此,整个格点模型就可以转化为1个由节点和电阻连接起来的电阻网络模型[如图 3b)右图所示]。两相邻节点间的电阻和电导计算公式如式(4) 和(5)。
| $ {R_{i,j}} = 0.5{R_i} + 0.5{R_j} = 0.5\left( {\frac{1}{{{g_i}}} + \frac{1}{{{g_j}}}} \right) $ | (4) |
| $ {g_{i,j}} = \frac{1}{{{R_{i,j}}}} = \frac{{2 \times {g_i} \times {g_j}}}{{{g_i} + {g_j}}} $ | (5) |
|
| 图 3 电阻网络模型的生成过程示意图 Figure 3 Generation of the random resistor network |
| |
i和j表示2个相邻的格点,Ri和gi分别表示格点i的电阻和电导;Rj和gj分别表示格点j的电阻和电导;Ri, j,gi, j分别表示相邻节点间的电阻和电导。
1.2 电导率的计算根据基尔霍夫定律,对于电路中的任一节点,任一瞬间流入和流出该节点的所有电流的代数和恒为0。
| $ \sum\limits_{k = 1}^6 {({U_{ik}} - {U_i}){g_{i,ik}}} = 0 $ | (6) |
其中,i表示电阻网络中的任一节点,ik表示与节点i相邻的节点,Ui表示节点i处的电势,Uik表示节点ik处的电势,gi, ik表示节点i与节点ik之间的电导。
将模型Z方向上边界处电势设为U(本研究中U=10 V),Z方向下边界处电势设为0,其他边界设为绝缘边界。通过求解方程组(6) 可以得到电阻网络中任一节点处的电势,从而可以得到Z方向上相邻两层节点之间的电流总值(以下简称为层间电流,对于N×N×N三维随机电阻网络模型,层间电流共有N-1个)。各层间电流Ii计算公式为:
| $ {l_i} = \sum\limits_{x = 1}^N {\sum\limits_{y = 1}^N {{I_{x,y,(i + 1,i)}}} } $ | (7) |
其中i=1, 2, 3, …, N-1。Ix, y, (i+1, i)表示第i+1层上节点(x, y, i+1) 与第i层上相邻节点(x, y, i)之间的电流。x,y表示节点在X,Y方向上的坐标(x=1, 2, 3…, N;y=1, 2, 3…, N)。
我们采用直接迭代法求解方程组(6),收敛条件是:
| $ {\rm{Potentialerror}} = {\rm{max}}(|U_i^n - U_i^{n + 1}|) < 0.0001 $ | (8) |
Uin和Uin+1分别表示第n次和第n+1次迭代结束时节点i的电势值。考虑到稳态下流过任一垂直于Z轴截面的电流实际上应相等,计算得到的各层间电流应足够接近。本计算中要求:
| $ {\rm{Currenterror}} = \frac{{{\rm{max}}({I_i}) - {\rm{min}}({I_i})}}{{{\rm{min}}({l_i})}} < 0.001 $ | (9) |
计算过程中,我们发现层间电流的算术平均值Iave随迭代次数的增加呈现双曲线的收敛趋势。为了减小误差,利用最小二乘法拟合得到Iave关于迭代次数的双曲线函数,并将其收敛极值Ifit作为流过模型Z方向的电流。进而利用Ifit以及加载在模型Z方向两端的电压U计算电阻网络整体的电导率,即DCO-碳酸盐复合电解质的电导率:
| $ {\sigma _{{\rm{com}}}} = \frac{{{l_{{\rm{fit}}}}}}{U} \times \frac{L}{S} = \frac{{{l_{{\rm{fit}}}}}}{U}/\left( {Nl} \right) $ | (10) |
其中L表示DCO-碳酸盐复合电解质的厚度,模型中L的值为Nl;S表示复合电解质垂直于Z轴的截面积,模型中为(Nl)2;σcom表示复合电解质的电导率。
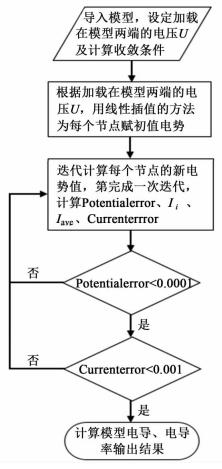
模型的生成程序及复合电解质电导率的计算程序均是通过Matlab 2010高级语言编写而成。复合电解质电导率的计算流程如图 4所示。
|
| 图 4 电导率计算流程图 Figure 4 Flow chat for conductivity calculation |
| |
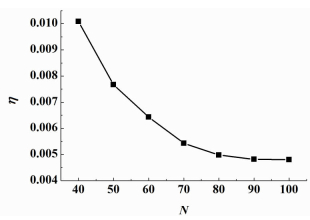
格点模型中每一维度上的格点数N对计算结果的稳定性有很大的影响,因此首先对N的大小进行了确定。计算结果的稳定性以多次计算结果的标准差与其平均值的比值η来表示:
| $ \eta = \frac{S}{{{\sigma _{{\rm{ave}}}}}} $ | (11) |
其中S表示多次计算结果的标准差,σave表示多次计算结果的平均值。碳酸盐与DCO电导率比值为100、碳酸盐体积分数为0.5时,η随N的变化关系如图 5所示。
|
| 图 5 计算结果的稳定性随N的变化关系 Figure 5 Dependence of η on N |
| |
从图 5中可以看出η随着N的增大而减小,N≥80时,η < 0.005,说明此时计算结果具有很好的稳定性。考虑到随着N的增大,达到计算精度所需的计算时间会急剧增加,故选取N=80。
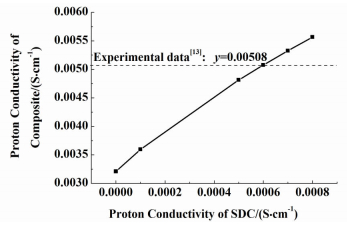
碳酸盐的含量、DCO颗粒的大小、温度对复合电解质的导电性能有很大影响。本研究主要计算了复合电解质的电导率随这3种因素的变化关系。计算所用的数据,SDC的O2-电导率σO2-SDC、熔融碳酸盐的O2-电导率σO2-Car和熔融碳酸盐的H+电导率σCarH+,来自Zhao等[13]的实验,其中σO2-SDC=8.0×10-3 S/cm,αO2-Car=6.7×10-2 S/cm,σCarH+=4.02×10-2 S/cm。但是未见有文献报道SDC的质子电导率σSDCH+。文献[13]中指出碳酸盐体积分数为0.473时,SDC和碳酸盐的颗粒粒径均约为100 nm。因此,在碳酸盐相的体积分数为0.473,k=1的条件下,利用Zhao等[13]测得的σCarH+和复合电解质的质子电导率对σSDCH+进行了选取。此条件下,σSDCH+对复合电解质的质子电导率的影响如图 6所示。
|
| 图 6 SDC质子导电率σH+SDC对复合电解质的质子电导率的影响 Figure 6 Influence of σH+SDC on proton conductivities of the composite electrolytes |
| |
从图 6中可以看出,复合电解质的质子电导率随着σSDCH+的增大而增大,且σSDCH+=6×10-4 S/cm时,计算值与实验值[13]刚好吻合,因此选取σSDCH+=6×10-4 S/cm。
碳酸盐相体积分数XCar及SDC与碳酸盐颗粒的粒径比k对复合体系O2-电导率的影响如图 7a)所示。从图 7a)中可以看出,随着XCar的增大,复合电解质的电导率逐渐增大。并且XCar一定时,随着SDC粒径的增大,复合电解质的电导率逐渐增大。这是因为SDC粒径越大,被SDC颗粒隔离的碳酸盐颗粒越少,而能够形成通路的碳酸盐相格点越多。碳酸盐相体积分数XCar及粒径比k对复合体系H+电导率的影响[如图 7b)所示]也具有相同的趋势。

|
| 图 7 碳酸盐体积分数及SDC粒径大小对复合电解质O2-电导率a)和H+电导率b)的影响 Figure 7 Effect of carbonate volume fraction and SDC particle size on O2- a) and H+ b) conductivities of SDC-Carbonate composite electrolytes |
| |
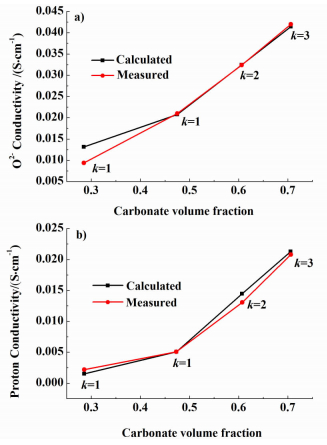
碳酸盐体积分数不同时,SDC-碳酸盐复合电解质的氧离子电导率的计算值与实验值[13]的对比如图 8a)所示。从图 8a)中可以看出,当计算值与实验值吻合时,随着碳酸盐体积分数的增大,SDC相颗粒的粒径逐渐增大。在相应粒径比下,复合电解质质子电导率的计算值与实验值也具有较好的吻合性[如图 8b)所示],说明σSDCH+=6×10-4 S/cm是合适的。
对于碳酸盐质量分数为20%的SDC-碳酸盐复合电解质(SDC-20LN),其氧离子电导率随温度的变化关系如图 9所示。计算时所用的SDC的O2-电导率和碳酸盐的O2-电导率来自Zhao等[13]的实验数据,如图 9中的SDC和Carbonate代表的曲线所示。从图 9中可以看出,复合电解质的O2-电导率随温度的升高而增大,且计算值与实验值[13]具有很好的吻合性。

|
| 图 9 碳酸盐质量分数为20%的复合电解质O2-电导率随温度的变化关系 Figure 9 Temperature dependence of O2- conductivities in SDC-20LN composite electrolytes |
| |
依据O2-和H+均能通过SDC和熔融碳酸盐体相传导的事实,首次用两相随机格点模型模拟掺杂氧化铈-碳酸盐复合电解质,进而将格点模型转化为电阻网络模型,对掺杂氧化铈-碳酸盐复合电解质导电性能进行了模拟,并考察了碳酸盐相的体积分数、SDC颗粒的粒径大小、温度对SDC-碳酸盐复合电解质电导率的影响。结果表明,复合电解质的电导率随碳酸盐体积分数的增大而增大,随SDC颗粒的增大而增大,随温度的升高而增大。并且复合电解质的电导率的计算值与实验值具有较好的吻合性,这表明格点模型和电阻网络模型是分析研究掺杂氧化铈-碳酸盐复合电解质导电行为的有效工具。
| [1] | Kharton V V, Marques F M B, Atkinson A. Transport properties of solid oxide electrolyte ceramics: A brief review[J]. Solid State Ionics, 2004, 174(1): 135–149. |
| [2] | Inaba H, Tagawa H. Ceria-Based solid electrolytes[J]. Solid State Ionics, 1996, 83(1): 1–16. |
| [3] | Liu X, Zhu B, Xu J, et al. Sulphate-Ceria composite ceramics for energy environmental co-generation technology[J]. Key Engineering Materials, 2004, 280: 425–430. |
| [4] | Zhu B. Functional ceria-salt-composite materials for advanced ITSOFC applications[J]. Journal of Power Sources, 2003, 114(1): 1–9. DOI: 10.1016/S0378-7753(02)00592-X |
| [5] | Zhu B, Liu X, Zhou P, et al. Innovative solid carbonate-ceria composite electrolyte fuel cells[J]. Electrochemistry Communications, 2001, 3(10): 566–571. DOI: 10.1016/S1388-2481(01)00222-3 |
| [6] | Zhao Y, Xia C, Xu Z, et al. Validation of H+/O2- conduction in doped ceria-carbonate composite material using an electrochemical pumping method[J]. International Journal of Hydrogen Energy, 2012, 37(15): 11378–11382. DOI: 10.1016/j.ijhydene.2012.05.015 |
| [7] | Zhu B, Albinsson I, Andersson C, et al. Electrolysis studies based on ceria-based composites[J]. Electrochemistry Communications, 2006, 8(3): 495–498. DOI: 10.1016/j.elecom.2006.01.011 |
| [8] | Zhu B, Mat M D. Studies on dual phase ceria-based composites in electrochemistry[J]. International Journal of Electrochemical Sciences, 2006, 1(8): 383–402. |
| [9] | Zhu B. Next generation fuel cell R&D[J]. International Journal of Energy Research, 2006, 30(11): 895–903. DOI: 10.1002/(ISSN)1099-114X |
| [10] | Zhu B, Li S, Mellander B E. Theoretical approach on ceria-based two-phase electrolytes for low temperature (300~600 C) solid oxide fuel cells[J]. Electrochemistry Communications, 2008, 10(2): 302–305. DOI: 10.1016/j.elecom.2007.11.037 |
| [11] | Liu W, Liu Y, Li B, et al. Ceria (Sm3+, Nd3+)/carbonates composite electrolytes with high electrical conductivity at low temperature[J]. Composites Science and Technology, 2010, 70(1): 181–185. DOI: 10.1016/j.compscitech.2009.10.006 |
| [12] | Zhao Y, Xia C, Wang Y, et al. Quantifying multi-ionic conduction through doped ceria-carbonate composite electrolyte by a current-interruption technique and product analysis[J]. International Journal of Hydrogen Energy, 2012, 37(10): 8556–8561. DOI: 10.1016/j.ijhydene.2012.02.053 |
| [13] | Zhao Y, Xu Z, Xia C, et al. Oxide ion and proton conduction in doped ceria-carbonate composite materials[J]. International Journal of Hydrogen Energy, 2013, 38(3): 1553–1559. DOI: 10.1016/j.ijhydene.2012.11.004 |
| [14] | Yin H, Tang D, Zhu H, et al. Production of iron and oxygen in molten K2CO3-Na2CO3 by electrochemically splitting Fe2O3 using a cost affordable inert anode[J]. Electrochemistry Communications, 2011, 13(12): 1521–1524. DOI: 10.1016/j.elecom.2011.10.009 |
| [15] | Tang D, Yin H, Xiao W, et al. Reduction mechanism and carbon content investigation for electrolytic production of iron from solid Fe2O3 in molten K2CO3-Na2CO3 using an inert anode[J]. Journal of Electroanalytical Chemistry, 2013, 689: 109–116. DOI: 10.1016/j.jelechem.2012.11.027 |
| [16] | Wang X, Ma Y, Li S, et al. Ceria-Based nanocomposite with simultaneous proton and oxygen ion conductivity for low-temperature solid oxide fuel cells[J]. Journal of Power Sources, 2011, 196(5): 2754–2758. DOI: 10.1016/j.jpowsour.2010.11.033 |
| [17] | Huang J, Mao Z, Yang L, et al. SDC-Carbonate composite electrolytes for low-temperature SOFCs[J]. Electrochemical and Solid-State Letters, 2005, 8(9): A437–A440. DOI: 10.1149/1.1960139 |
| [18] | Liu R, Xie Y, Wang J, et al. Synthesis of ammonia at atmospheric pressure with Ce0.8M0..2O2-δ(M=La, Y, Gd, Sm) and their proton conduction at intermediate temperature[J]. Solid State Ionics, 2006, 177(1): 73–76. |
| [19] | Sun W, Shi Z, Liu W. Considerable hydrogen permeation behavior through a dense Ce0.8Sm0.2O2-δ(SDC) asymmetric thick film[J]. Journal of the Electrochemical Society, 2013, 160(6): F585–F590. DOI: 10.1149/2.073306jes |
 2017, Vol. 34
2017, Vol. 34