油水分离应用于许多工业过程的分离操作部分[1]。聚结即多个小液滴融合成1个较大液滴的过程,是油水分离过程中的常见现象。通常,由于油水两相不互溶,在重力的作用下,最终可以实现两相的分离。然而,当分散相为乳化态液滴时(粒径小于100 μm),布朗运动的影响愈发显著,经典的斯托克斯方程不再适用,分散相液滴可以长期稳定地悬浮在混合液中[2]。这时则需要采用聚结法来实现分散相的聚结。
采用聚结法,即在一定乳化程度的乳化液流经聚结材料时,分散相液滴就可以被聚结材料吸附并在其表面富集发生聚结,增大自身粒径,从而有利于快速高效地被分离出来[3]。该方法利用油水两相对聚结材料的亲和力不同进行分离,不同种类的聚结材料以及具有不同外形的同一种聚结材料,都会影响分离效果[4]。由此可见,聚结法的技术关键是选择合适的聚结材料,而材料的表面润湿性即油相或水相液体附着到材料表面的倾向性则是需要重点考虑的因素。
目前,在众多的聚结材料中,纤维材料的应用时间较早且范围广泛[5]。随着高分子合成工业的快速发展,合成纤维性能优良且产品质量易于控制,越来越多地被用作聚结材料[6]。因此,本研究选择3种主要合成纤维作为研究对象。
关于表面润湿性的研究中,大多以表面能作为判断依据[7]。然而至今仍无精确、可靠、通用的测定固体表面能的方法,目前研究中使用的方法均只适用于一定条件下的特定体系[8]。通常是通过测试接触角间接计算得出结果[9]。但是合成纤维并不具备接触角法所要求的光滑平整均匀的表面,并且其对液体的吸收也增大了结果的误差[10]。
使用反相气相色谱法可以避免上述问题。该方法快速有效[11],可以在较宽的温度范围内测定多种固体材料的表面自由能及其他热力学函数,并且只需要很少量的材料样品和试剂[12]。在过去的50年中,该方法得到了很好的理论发展和实际应用[13]。
国内外众多研究者已经将反相气相色谱法用于表征高聚物材料、天然和无机纤维、氧化物颗粒等固体材料的性质,表征结果多用于增强固体材料表面性能,评价固体材料改性效果以及预测固体材料与其复合物质界面间的相互作用等方面。目前尚无将反相气相色谱法应用于固体材料表面润湿性的表征。
本研究首次将反相气相色谱法应用于表征合成纤维表面润湿性,测定了聚丙烯纤维、聚癸二酰己二胺纤维和聚对苯二甲酸乙二醇酯纤维的表面自由能色散分量和水分子的净保留体积,以此判断其对油水两相亲和性的不同,并探究了温度、纤维化学结构单元以及纱线线体结构对表面润湿性的影响。
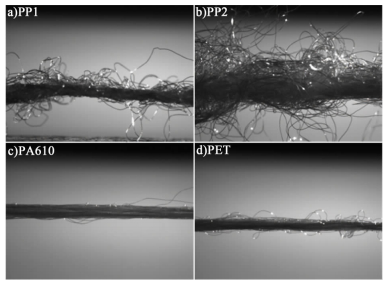
1 材料与方法 1.1 实验材料聚丙烯纤维(具有2种外观形态,分别记为PP1和PP2),聚癸二酰己二胺纤维(PA610),聚酯纤维即聚对苯二甲酸乙二醇酯纤维(PET),均购于东台邦德化纤有限公司,呈纱线形式(外观形貌见图 1),纱线的主要性质见表 1。
|
| 图 1 纱线的外观形貌 Figure 1 Exterior appearance of the yarns |
| |
| 合成纤维 | 纱线类型 | 线密度/tex | 纤维细丝直径/μm |
| PP1 | 毛圈纱 | 145 | 25.65 |
| PP2 | 毛圈纱 | 390 | 24.58 |
| PA610 | 长丝纱 | 130 | 16.56 |
| PET | 长丝纱 | 131 | 12.68 |
正己烷、正庚烷、正辛烷、正壬烷,均为色谱标定纯,购于天津市光复精细化工研究所;蒸馏水,购于永源蒸馏水制造中心。
气相色谱仪(北京北分天普仪器技术有限公司SP-3420型);循环水式多用真空泵(上海翔雅仪器设备有限公司SHB-ⅢA型);电子天平(上海天平仪器厂YP1002N型)。
1.3 试验过程 1.3.1 反相气相色谱柱的制备采用聚四氟乙烯柱,内径6 mm,长度30 cm。将待测纤维材料剪切成平均长度为4~5 mm的短线段,采用真空填充法将剪切后的纤维装入色谱柱中。色谱柱在进行测试前需要老化,断开色谱柱与检测器连接,使用氢气为载气,调整速率为7~8 mL/min。先在常温下,用氢气吹扫2 h;之后升高柱温至100 ℃,老化12 h。
1.3.2 反相气相色谱分析条件调整载气速率为15 mL/min左右。选用热导检测器,检测器与进样器温度设定为150 ℃。一系列正烷烃作为探针分子时,进样量为1 μL,柱温范围为60~80 ℃;水分子作为探针分子时,进样量为0.1 μL,柱温范围为90~110 ℃。气相色谱图最大峰值出现的时间即为要测定的停留时间。
1.3.3 计算方法探针分子的校准保留体积可由式(1) 计算。
| $ {V_{\rm{N}}} = j\cdot\frac{{F({t_{\rm{R}}} - {t_{\rm{M}}})}}{M}\cdot\frac{{{T_{\rm{C}}}}}{{{T_{\rm{F}}}}}\cdot\frac{{P - {P_{\rm{F}}}}}{P} $ | (1) |
式(1) 中,j为James-Martin气体压缩校正因子;F为载气的体积流率,mL/min;tM是死时间(即不与固定相发生交互作用的探针分子通过色谱柱的时间),min;tR是正烷烃和蒸馏水作为探针分子时的停留时间,min;M为色谱柱中合成纤维的填充质量,g;TC和TF分别为柱温与皂膜流量计所处环境温度(一般为室温),K;P是色谱柱出口处压力,kPa;PF为皂膜流量计所处环境温度下的水的饱和蒸汽压,kPa。
合成纤维的表面能色散分量(γSd)的计算如下:
根据Dorris和Gray[14]的计算方法,正烷烃在材料表面的吸附自由能可由式(2) 计算。
| $ \Delta {G_{\rm{A}}} = - RT{\rm{ln}}{V_{\rm{N}}} + C $ | (2) |
式(2) 中,R为气体常数,J/(mol·K);C为常数。
已知ΔGA与正烷烃分子所含的碳原子数有很好的线性关系,将RTlnVN与碳原子数作图,所得直线的斜率即为ΔGA的值。
依据Fowkes[15]的研究,探针分子在固定相材料表面的吸附自由能主要由色散相互作用和酸-碱相互作用组成。二者的主要作用力分别是London力和氢键。正烷烃是非极性分子,则可认为其与材料表面只有色散相互作用。因此正烷烃的表面吸附自由能可以用来计算合成纤维的表面能色散分量。
合成纤维的表面能色散分量γSd可由式(3) 计算:
| $ \frac{{\Delta {G_{\rm{A}}}}}{{N{a_{{\rm{C}}{{\rm{H}}_{\rm{2}}}}}}} = \frac{{RT{\rm{ln}}{V_{\rm{N}}}}}{{N{a_{{\rm{C}}{{\rm{H}}_{\rm{2}}}}}}} = 2{({\gamma _{{\rm{C}}{{\rm{H}}_{\rm{2}}}}}\gamma _{\rm{S}}^{\rm{d}})^{1/2}} $ | (3) |
式(3) 中,N为阿伏伽德罗常数;aCH2为单个亚甲基基团与固定相表面接触的横截面积,是固定值为0.06 nm2,表示仅由亚甲基基团构成的液体物质的表面张力,mJ/m2,具体数值可由式(4) 计算:
| $ {\gamma _{{\rm{C}}{{\rm{H}}_{\rm{2}}}}} = 35.6 - ({T_{\rm{C}}} - 293.15) $ | (4) |
另一种计算方法来自Schultz等[16],合成纤维的表面能色散分量γSd可由式(5) 计算。
| $ \frac{{\Delta {G_{\rm{A}}}}}{{N{a_{\rm{s}}}}} = \frac{{RT{\rm{ln}}{V_{\rm{N}}}}}{{N{a_{\rm{s}}}}} = {W_{\rm{A}}} = 2{(\gamma _{\rm{L}}^{\rm{d}}\gamma _{\rm{S}}^{\rm{d}})^{1/2}} $ | (5) |
式(5) 中,as为探针分子的表面积,m2;γLd为探针分子为液态时在相应柱温t(℃)下的表面张力,mJ/m2,具体数值由兰氏化学手册查得[17],见表 2。
| 探针分子 | a/(10-20m2) | γdL(=a-bt)/(mJ·m-2) | |
| a | b | ||
| C6H14 | 51.5 | 20.44 | 0.1022 |
| C7H16 | 57.0 | 22.10 | 0.0980 |
| C8H18 | 62.8 | 23.52 | 0.0951 |
| C9H20 | 68.9 | 24.72 | 0.0935 |
同样,由(5) 式可以看出RTlnVN与as(γdL)1/2有很好的线性关系,将二者作图,所得直线的斜率可直接得到γSd的数值。
2 结果及讨论 2.1 合成纤维的表面能色散分量(γSd)使用Dorris和Gray的方法和Schultz等的方法计算出γSd,结果见表 3。
| 合成纤维 | 方法 | γSd/(mJ·m-2) | ||||
| 60 ℃ | 65 ℃ | 70 ℃ | 75 ℃ | 80 ℃ | ||
| PP 1 | 1 | 53 | 58 | 61 | 64 | 63 |
| 2 | 49 | 54 | 56 | 59 | 57 | |
| PP 2 | 1 | 45 | 52 | 61 | 62 | 66 |
| 2 | 42 | 49 | 55 | 57 | 60 | |
| PA610 | 1 | 46 | 45 | 44 | 43 | 39 |
| 2 | 43 | 42 | 41 | 40 | 36 | |
| PET | 1 | 46 | 35 | 34 | 25 | 23 |
| 2 | 43 | 32 | 31 | 23 | 21 | |
| 注:方法1: Dorris和Gray的计算方法; 方法2: Schultz等的计算方法。 | ||||||
依照Dorris和Gray的计算方法得出的γSd要大于依照Schultz等的计算方法得出的γSd,但2种方法所得的γSd较为接近,其相差数值与Schultz等[16]、Asten等[18]和Tsutsumi等[19]的研究结果具有较好的一致性,并且通过2种方法得到的γSd随温度的变化趋势完全相同。因此可以确定反相气相色谱法适用于本研究,所得数值准确可靠。
以由Dorris和Gray的计算方法得出的γSd为例,PP1和PP2的γSd较大,其范围为45~66 mJ/m2,PA610和PET的γSd较小,范围分别为39~46 mJ/m2和23~46 mJ/m2。γSd代表着纤维表面对非极性分子作用力的大小,γSd越大,表明相互作用力越大。依据固体表面润湿理论,固体表面与气体分子之间的相互作用力要大于液体与气体分子之间相互作用力(即液体的表面张力),固体才可以被液体润湿。以正烷烃为主要组成的油相液体表面张力较低,则γSd越大的合成纤维对油相液体的亲和力越好。因此,γSd较大的PP1和PP2有较好的亲油性,而PA610和PET的亲油性则较差。
2.1.1 纤维化学结构单元对γSd的影响不同的合成纤维其化学结构单元不同,其化学构成各异是造成γSd显著差异的根本原因。PP1和PP2的结构单元由亚甲基和甲基构成,均为非极性基团,更容易与非极性的正烷烃分子通过London力产生较强的相互作用,因此γSd较大;PA610的结构单由亚甲基和酰胺基构成,亚甲基与正烷烃分子之间存在较强的相互作用,但是1个分子链上的酰胺基团中的氢原子可以与另1个分子链中酰胺基团的氧原子形成氢键,导致PA分子链间的相互作用力非常强,影响了与正烷烃之间的作用力,所以PA610的γSd要小于PP1和PP2的γSd。PET的结构单元由亚甲基、酯基、苯环、端醇羟基构成,其中,亚甲基与苯环为非极性基团,可以与正烷烃分子发生较强的相互作用,但酯基是极性基团,增强了分子间的相互作用力,在一定程度上减弱了PET对正烷烃分子的作用力,因而PET的γSd也小于PP1和PP2的γSd。
2.1.2 纱线线体结构对γSd随温度变化趋势的影响纱线的线体结构不同,其γSd随着温度有不同的变化趋势。
PA610与PET为长丝纱,二者的γSd随着温度的升高而减小,这是因为纤维受热膨胀,纤维本体分子间的相互作用力增强,从而减弱了表面分子对探针分子的作用力。
PP1和PP2均为毛圈纱,PP1的γSd随温度升高先增大后减小(由53 mJ/m2升高至64 mJ/m2后降低为63 mJ/m2),PP2的γSd随温度升高一直增大(由45 mJ/m2升高至66 mJ/m2)。本研究认为出现这种情况,纱线线体结构是主要影响因素。由图 1可看出,PP1和PP2纱线线体较为蓬松,具有大量弯曲的纤维细丝,二者纤维细丝直径相差很小可以认为相同,而PP2的线密度约为PP1的线密度的2.5倍。当处在受热环境当中,纱线线体与纤维表面同时受热膨胀,但二者膨胀后对γSd造成的影响不同:蓬松的线体具有较大的膨胀空间,膨胀时,体积明显增大,纤维细丝之间的空隙增大,甚至弯曲的纤维细丝也伸展开来,从而增大了与探针分子的作用面积,表现为γSd的增大;纤维表面的膨胀则与PA610与PET的情况一样,造成γSd的减小。在一定的温度范围内,纱线线体膨胀所造成的影响远大于纤维表面膨胀的影响,故而γSd随温度升高而增大;当温度升高到一定程度,纱线线体完全膨胀,因其所造成的对γSd的影响减弱,纤维表面膨胀的影响开始占主导地位,则γSd随温度的继续升高而减小,其变化趋势中出现拐点,如PP1。因为PP2的线密度远大于PP1,在所测定的温度范围内,其线体没有实现完全膨胀,故γSd仍在升高。
此外,对比同温度下PP1与PP2的γSd可以发现,在低于80 ℃的温度范围内,PP2的值小于或等于PP1的值,在80 ℃时,PP2的值才大于PP1的值。这说明线密度大并不一定代表纤维与正烷烃分子的相互作用力强,在受热膨胀不显著的时候,线密度大的纱线可能因为纤维的互相遮挡掩盖,反而减弱了其对正烷烃分子的相互作用。
2.2 水分子的净保留体积(VN)为了尽量避免水分子在合成纤维表面的凝结并综合考虑色谱柱和合成纤维的耐热性,本研究在100~110 ℃的范围内测定了水分子的净保留体积,结果见表 4。
| 合成纤维 | VN/mL | ||
| 100 ℃ | 100 ℃ | 100 ℃ | |
| PP1 | 1.43 | 1.11 | 0.35 |
| PP2 | 0.91 | 0.77 | 0.17 |
| PA610 | 41.03 | 31.36 | 26.35 |
| PET | 24.77 | 19.01 | 14.71 |
VN的大小可以直接反映合成纤维与水分子的相互作用情况,VN越大,表明相互作用力越强。PA610的VN最大,范围为26.35~41.03 mL,说明PA610对水分子有较强的相互作用,是亲水性材料,PET的VN范围为14.71~24.77 mL,表明其亲水性比PA610要差,而PP1和PP2的VN非常小,范围为0.17~1.43 mL,说明其几乎不与水分子发生相互作用,亲水性非常差。
2.2.1 纤维化学结构单元对VN的影响纤维化学结构单元对VN有决定性影响:PA610结构单元中的亚甲基与水分子相互作用力非常弱,但大量酰胺键能与水分子形成稳定的氢键作用,故PA610亲水性最好,并且,我们还可以推断其他类型的聚酰胺纤维如PA6、PA66等,纤维所含的酰胺基与亚甲基的比例越大,则其亲水性越好;PET结构单元中的酯基是极性基团,其碳氧双键中碳原子的电子云偏向氧原子,因而具有一定的亲水性,但苯环的空间位阻大,阻碍酯基与水分子的结合,所以与水分子的之间作用弱;PET的端醇羟基虽然可以形成氢键,但单体聚合后,只存在很少量的端醇羟基,故PET的亲水性不如PA610好;PP1与PP2的结构单元全部由非极性基团构成,没有显著的电偶极矩,与水分子的相互作用力非常微弱,所以其亲水性最差。
2.2.2 温度和纱线线体结构对的VN的影响4种合成纤维的VN均随着温度的升高而减小,这表明升高温度会减弱其与水分子之间的相互作用。但是低温条件下,水分子在合成纤维表面的凝结效果将十分明显,严重影响实验结果的准确性。因此,应综合考虑凝结作用和温度的影响。
同种合成纤维中,PP1的VN(0.35~1.43 mL)大于PP2的VN(0.17~0.91 mL)。依照上文的测定结果,PP1的纱线线体已经完全膨胀,PP2的纱线线体也有了一定程度的膨胀,这说明在线体膨胀程度较高的情况下,线密度较大的PP2与水分子的相互作用更微弱,亲水性更差。本研究所使用的合成纤维均已实现工业化生产,但受生产条件、市场需求等方面的限制,合成纤维的外形样式较为单一,本研究只针对PP的2种纤维外形进行了对比分析。如果能够取得具有多种外形样式的同种纤维,其外形对合成纤维表面润湿性的影响将会是一个非常有意义的研究方向。
另外,水分子的净保留体积与合成纤维填充量、填充柱尺寸、柱前压等因素有关,使用不同的填充柱或色谱仪,测定的VN将会不同,该方法只能在检测条件完全相同的情况下判断不同合成纤维的亲水性,不具备普遍适用性。因此,使用反相气相色谱表征合成纤维亲水性的研究方法仍有待进一步完善。
3 结论本研究使用反相气相色谱法测定合成纤维表面自由能色散分量和水分子的净保留体积,建立了判断合成纤维表面润湿性的方法,并得出以下结论。
1) 合成纤维的化学结构单元对其润湿性起着决定性作用:表面的极性基团使纤维具有亲水性;非极性基团使纤维具有亲油性。
2) 纱线线体结构影响着表面自由能色散分量随温度的变化及水分子的净保留体积:长丝纱的表面自由能色散分量随温度升高而减小;毛圈纱的表面自由能色散分量随温度升高先增大后减小;在受热膨胀较充分的情况下,线密度较大的毛圈纱中,水分子的净保留体积较小,其亲水性更差。
本研究的理论意义在于提出了一种能够准确判断合成纤维表面润湿性的新方法,弥补了现有聚结材料表面润湿性测定方法的不足,对聚结机理的探索和完善具有参考价值;本研究的实用意义则在于为选择聚结材料提供可靠依据,并对改进聚结材料和优化聚结方法具有指导意义。
| [1] | Cusack R. Rethink your liquid-liquid separations[J]. Euromoney Trading Limited, 2009, 88(6): 53–60. |
| [2] | Bansal S, Arnim V V, Stegmaier T, et al. Effect of fibrous filter properties on the oil-in-water-emulsion separation and filtration performance[J]. Journal of Hazardous Materials, 2011, 190(1): 45–50. |
| [3] | Ristenpart W D, McCalla P M, Roy R V, et al. Coalescence of spreading droplets on a wettable substrate[J]. Physical Review Letters, 2006, 97(6): 3633–3646. |
| [4] |
纪轩.
废水技术处理问答[M]. 北京: 中国石化出版社, 2003 Ji Xuan. Wastewater technology treatment questions and answers[M]. Beijing: China Petrochemical Press, 2003. |
| [5] |
刘亚莉, 吴山东, 戚俊清, 等. 用于油水分离的聚结技术及其进展[J].
西南石油大学学报:自然科学版, 2008(1): 129–132.
Liu Yali, Wu Shandong, Qi Junqing, et al. Coalescence techniques and progress for the oil-water separation[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2008(1): 129–132. |
| [6] | 周建. 聚结技术处理含油污水的实验研究[D]. 北京: 中国石油大学, 2009 Zhou Jian. Study on Treatment of oily wastewater by coalescence technology[D]. Beijing: China University of Petroleum, 2009 (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10425-2009222528.htm |
| [7] |
王正烈, 周亚平.
物理化学[M]. 北京: 高等教育出版社, 2001 Wang Zhenglie, Zhou Yaping. Physical chemistry[M]. Beijing: Higher Education Press, 2001. |
| [8] |
赵振国.
应用胶体与界面化学[M]. 北京: 化学工业出版社, 2008 Zhao Zhenguo. Application of colloid and interface chemistry[M]. beijing: Chemical Industry Press, 2008. |
| [9] |
汪成, 王淑红, 金政.
先进聚合物基复合材料及应用[M]. 哈尔滨: 哈尔滨地图出版社, 2009 Wang Cheng, Wang Shuhong, Jin Zheng. Advanced polymer matrix composite materials and applications[M]. Harbin: Harbin Map Press, 2009. |
| [10] | Anhang J, Gray D G. Surface characterization of poly (ethylene terephthalate) film by inverse gas chromatography[J]. Journal of Applied Polymer Science, 1982, 27(1): 71–78. DOI: 10.1002/app.1982.070270108 |
| [11] | Donnet J B, Park S J, Balard H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography[J]. Chromatographia, 1991, 31(9/10): 434–440. |
| [12] | Heng J, Pearse D F, Thielmann F, et al. Methods to determine surface energies of natural fibres: A review[J]. Composite Interfaces, 2007, 14(7/9): 581–604. |
| [13] | Voelkel A, Strzemiecka B, Adamska K, et al. Inverse gas chromatography as a source of physiochemical data[J]. Journal of Chromatography A, 2009, 1216(10): 1551–1566. DOI: 10.1016/j.chroma.2008.10.096 |
| [14] | Dorris G M, Gray D G. Adsorption of n-alkanes at zero surface coverage on cellulose paper and wood fibers[J]. Journal of Colloid and Interface Science, 1980, 77(2): 353–362. DOI: 10.1016/0021-9797(80)90304-5 |
| [15] | Fowkes F M. Calculation of work of adhesion by pair potential suummation[J]. Journal of Colloid and Interface Science, 1968, 28(3): 493–505. |
| [16] | Schultz J, Lavielle L, Martin C. The role of the interface in carbon fibre-epoxy composites[J]. The Journal of Adhesion, 1987, 23(1): 45–60. DOI: 10.1080/00218468708080469 |
| [17] | Speight J G. Lange's handbook of chemistry[M]. USA: McGraw-Hill New York, 2005. |
| [18] | Van Asten A, van Veenendaal N, Koster S. Surface characterization of industrial fibers with inverse gas chromatography[J]. Journal of Chromatography A, 2000, 888(1): 175–196. |
| [19] | Tsutsumi K, Ohsuga T. Surface characterization of modified glass fibers by inverse gas chromatography[J]. Colloid & Polymer Science, 1990, 268(1): 38–44. |
 2017, Vol. 34
2017, Vol. 34





