燃料电池是将燃料的化学能直接转化为电能的一种电化学反应装置,除了能量转化效率高以外,还具有能量转化过程较清洁、热效率高、应用范围广等优点。质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell,PEMFC)作为燃料电池的一种,除了具有各种燃料电池的共同优点外,还具有功率密度高、工作温度低、启动快、可靠性强等独特优势,因此在电动汽车和便携电器设备等方面具有广阔的应用前景。
PEMFC的核心部件——膜电极组件MEA(Membrane Electrode Assembly)——是由质子交换膜、阳极与阴极催化层和气体扩散层叠压在一起构成。催化层作为电化学反应发生的场所,是膜电极的关键组成部分。电极催化层由三相构成,分别是传导质子的离子聚合物相、传导电子的Pt/C催化剂相和传递气体的孔相。电化学反应只能发生在电子、质子与气体通路的交汇区域(三相区),因此催化层的各相组成及其中各成分的传输对电极反应有极大影响。了解催化层结构与其中物质传递和电化学反应的关系对于提高PEMFC的性能至关重要。目前的实验分析表征方法对研究催化层中的构效关系有很大局限性,而计算机数学模拟为此提供了重要的研究手段。
催化层的结构参数对其性能有很大影响,因此许多国内外的科学家对此进行了研究。目前,用于研究催化层参数影响的模型主要有界面模型[1-3]、宏观均相模型[4-10]、团聚体模型[11-16]以及近年发展起来的孔网络模型[17-19]和微观格点模型[20-25]等。Song等[7]利用宏观均相模型对PEMFC阴极催化层进行了单参数和双参数的数值优化,发现在0.6 V的电池电压下,当进行单参数优化时,PEMFC的性能对厚度参数十分敏感,10 μm的催化层性能最优;当进行催化层厚度与单位面积Pt载量双参数优化时,可以使电池获得最大的电能输出。Senanell等[16]基于二维团聚体模型研究了膜电极的参数优化问题。模拟结果显示,增加离子聚合物相的体积分数和Pt载量、减少催化层中的碳含量可以改善膜电极中的物质传递和电化学动力学。Wu等[19]利用孔网络模型模拟PEMFC阴极催化层,发现在低于1.0 A·cm-2的电流密度区,越薄的催化层所对应的电池性能越好;当电流密度高于1.0 A·cm-2时,电池性能却呈现相反的变化趋势。Zhang等[24]利用球形微观结构模型模拟了PEMFC的阴极催化层,并对催化层厚度和催化剂颗粒粒径进行了优化研究。
相比于界面模型,宏观均相模型考虑了催化层内厚度方向上的物质和电荷传递过程,模型的准确性有所提高;而相比于团聚体模型和微观模型,均相模型较简单,计算效率大大提高。因此,本研究采用宏观均相模型来模拟PEMFC的阴极催化层。
催化层厚度是一个和电池的活化极化、欧姆极化和浓差极化都息息相关的参数。其不但影响着催化层内部的物质和电荷传递,还关乎催化层内催化活性面积的大小。然而目前对催化层厚度影响的研究不够充分,一般是在特定电压或特定电流下分析讨论催化层厚度,没有得到在PEMFC全操作电流范围内适用的同一厚度。还有些只是笼统讨论催化层厚度影响而没有指出催化层厚度变化的具体方式。
本研究采用一维稳态的宏观均相模型模拟阴极催化层(CCL),进而研究催化层厚度对质子交换膜燃料电池(PEMFC)性能的影响。对具有不同厚度CCL的PEMFCs在全操作电流范围内的功率输出进行了计算,并获取了各催化层内的氧气浓度、氧气还原反应(ORR)速率和阴极过电位在催化层内的分布。因催化层各参数间是相互影响的,无法做到绝对的单一参数变化。为保持催化层各相体积分数不变,我们采用2种变化催化层厚度的方式,一是变化单位面积内的Pt载量mPt,另一种是变化Pt在碳载铂(Pt/C)催化剂颗粒中的质量分数f。2种方法都可以改变催化层内的催化活性面积大小。
1 数学模型 1.1 模型对象描述本研究的目标是探讨催化层厚度对PEMFC性能的影响,因此我们选择建立在厚度方向的单一维度模型。为了精简计算量,采用宏观均相模型模拟PEMFC的阴极催化层,图 1是CCL的示意图。
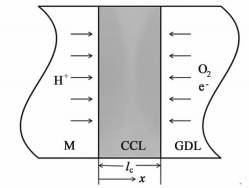
|
| 图 1 PEMFC阴极催化层的示意图 Figure 1 Schematic of the cathode catalyst layer for a PEMFC |
| |
我们考虑的PEMFC在恒温(80 ℃)、恒压(3/1atm H2/O2,1 atm=1.013×105 Pa,下同。)条件下稳态工作,其催化层由质子导体Nafion、电子导体Pt/C颗粒与孔隙三相构成并在催化层中均匀分布,形成质子、电子和气体的传递通路。催化层的孔隙不被液态水占据。
1.2 控制方程氧气在催化层中的扩散由浓度梯度驱使,其浓度分布服从Fick定律。因此,通过阴极催化层界面的氧气通量为:
| ${N_{{{\rm{O}}_2}}} =-D_{{{\rm{O}}_2}}^{{\rm{eff}}}\frac{{{\rm{d}}{c_{{{\rm{O}}_2}}}}}{{{\rm{d}}x}}$ | (1) |
其中,NO2是催化层垂直于厚度方向的氧气摩尔通量,cO2是催化层中的局部氧气浓度,x是沿厚度方向的坐标,如图 1所示。DeffO2是催化层内氧气的有效扩散系数,其与氧气在空气中扩散的本体扩散系数DO2之间满足Bruggeman关系式[26]:
| $D_{{{\rm{O}}_2}}^{{\rm{eff}}} = {{\rm{D}}_{{{\rm{O}}_2}}}\varepsilon _{\rm{V}}^{3/2}$ | (2) |
式(2) 中εV是催化层内孔相的体积分数。
稳态情况下,催化层厚度方向氧气摩尔通量的变化量等于电化学反应的消耗量,即单位体积内的电化学反应速率RO2。
| $\frac{{{\rm{d}}{N_{{{\rm{O}}_2}}}}}{{{\rm{d}}x}} = {R_{{{\rm{O}}_2}}}$ | (3) |
由质子的物料守恒,RO2与质子电流密度i之间存在如下关系:
| ${R_{{{\rm{O}}_2}}} =-\frac{1}{{nF}}\frac{{{\rm{d}}i}}{{{\rm{d}}x}}$ | (4) |
由此得到氧气浓度的分布方程:
| $\frac{{{\rm{d}}{c_{{{\rm{O}}_2}}}}}{{{\rm{d}}x}} = \frac{{i-{I_{{\rm{tot}}}}}}{{nFD_{{{\rm{O}}_2}}^{{\rm{eff}}}}}$ | (5) |
式(4)~(5) 中,n为氧还原反应转移的电子数,F为法拉第常数,Itot是电池的总电流密度。
电化学反应速率可由Butler-Volmer方程计算得出:
| $\frac{{{\rm{d}}i}}{{{\rm{d}}x}} = ai_0^{{\rm{ref}}}\frac{{{c_{{{\rm{O}}_2}}}}}{{c_{{{\rm{O}}_2}}^{{\rm{ref}}}}}\left[{\exp \left( {\frac{{{\alpha _{\rm{c}}}F{\eta _{\rm{c}}}}}{{RT}}} \right)-\exp \left( {-\frac{{{\alpha _{\rm{a}}}F{\eta _{\rm{c}}}}}{{RT}}} \right)} \right]$ | (6) |
式(6) 中a是催化层的活性比表面积,crefO2是参考氧气浓度,αc和αa分别是阴极和阳极的电荷转移系数,ηc是阴极催化层的过电位,i0ref是参考交换电流密度,可由对实验数据[27]的曲线拟合而得:
| $i_0^{{\rm{ref}}} = {10^{0.03741T-16.96}}$ | (7) |
催化层的活性比表面积a与催化剂载量mPt和催化层的厚度lc的关系为:
| $a = \frac{{{m_{{\rm{Pt}}}}}}{{{l_{\rm{c}}}}}{A_{\rm{s}}}$ | (8) |
式(8) 中As是单位质量Pt具有的反应活性面积,其与Pt在碳载铂(Pt/C)催化剂颗粒中的质量分数f有关[15]:
| $\begin{array}{c} {A_{\rm{s}}} = \left( {227.79{f^3}-158.57{f^2}-201.53f + } \right.\\ \left. {159.5} \right) \times {10^3} \end{array}$ | (9) |
| $f = \frac{{{m_{{\rm{pt}}}}}}{{{m_{{\rm{Pt}}}} + {m_{\rm{c}}}}}$ | (10) |
式(10) 中mC是单位面积催化层中的碳载量。
阴极过电位ηc与质子电势φP和电子电势φe、平衡电极电势Eeq, c有关,表示为:
| ${\eta _{\rm{c}}} = {\varphi _{\rm{c}}}-{\varphi _{\rm{P}}}-{E_{{\rm{eq, c}}}}$ | (11) |
对式(11) 进行微分,并结合欧姆定律[10]:
| $\frac{{{\rm{d}}{\varphi _{\rm{p}}}\varphi }}{{{\rm{d}}x}} =-\frac{i}{{{\kappa ^{{\rm{eff}}}}}}$ | (12) |
| $\frac{{{\rm{d}}{\varphi _{\rm{e}}}}}{{{\rm{d}}x}} =-\frac{{{I_{{\rm{tot}}}}-i}}{{{\sigma ^{{\rm{eff}}}}}}$ | (13) |
可得:
| $\frac{{{\rm{d}}{\eta _{\rm{c}}}}}{{{\rm{d}}x}} = \frac{i}{{{\kappa ^{{\rm{eff}}}}}} + \frac{{i-{I_{{\rm{tot}}}}}}{{{\sigma ^{{\rm{eff}}}}}}$ | (14) |
式(14) 中κeff是催化层的有效质子电导率,可由Nafion的本征质子电导率κH和其在催化层内的体积分数εN的Bruggeman关系式求得:
| ${\kappa ^{{\rm{eff}}}} = {\kappa _{\rm{H}}}\varepsilon _{\rm{N}}^{3/2}$ | (15) |
同样,催化层的有效电子导率σeff可通过催化剂固体相的本征电子导率σe与其在催化层内的体积分数εS的Bruggeman关系式求得:
| ${\sigma ^{{\rm{eff}}}} = {\sigma _{\rm{e}}}\varepsilon _{\rm{S}}^{3/2}$ | (16) |
式(16) 中εS可由催化剂载量mPt、催化层厚度lc、Pt在碳载铂(Pt/C)催化剂颗粒中的质量分数f、铂的密度ρPt和碳的密度ρC求得:
| ${\varepsilon _{\rm{S}}} = \left( {\frac{1}{{{\rho _{{\rm{Pt}}}}}} + \frac{{1-f}}{{f{\rho _C}}}} \right)\frac{{{m_{{\rm{Pt}}}}}}{{{l_c}}}$ | (17) |
另外,催化层中三相体积分数的和等于1,故其中孔隙率为:
| ${\varepsilon _{\rm{V}}} = 1-{\varepsilon _{\rm{N}}}-{\varepsilon _{\rm{S}}}$ | (18) |
在阴极催化层与质子交换膜的界面,即M/CCL界面(x=0),质子电流密度等于电池电流密度,而氧气的扩散通量为0:
| $i\left| {_{x = 0} = {I_{{\rm{tot}}}}} \right.$ | (19) |
| ${\left. {\frac{{{\rm{d}}{c_{{{\rm{O}}_2}}}}}{{{\rm{d}}x}}} \right|_{x = 0}} = 0$ | (20) |
在阴极催化层与气体扩散层的界面,即CCL/GDL界面(x=lc),质子电流密度为0,而氧气浓度为定值。
| $i\left| {_{x = {l_{\rm{c}}}} = 0} \right.$ | (21) |
| ${c_{{{\rm{O}}_2}}}\left| {_{x = {l_{\rm{c}}}} = {c_0}} \right.$ | (22) |
完成几何建模以后,借助Comsol Multiphysics 3.5软件对控制方程进行求解。计算所选用的基本参数归纳于表 1中。
| 参数 | 符号 | 单位 | 取值 |
| 法拉第常数 | F | C·mol-1 | 96 500 |
| ORR反应电子转移数 | n | 4 | |
| 普适气体常数 | R | J·mol-1·K-1 | 8.314 |
| 温度 | T | K | 353.15[5] |
| 氧气的压力 | PO2 | atm | 1 |
| H2压力 | PH2 | atm | 3[30] |
| CCL厚度 | lc | μm | 10 |
| Nafion相的体积分数 | εN | 0.3[7] | |
| 孔隙率 | εV | 0.25 | |
| 单位面积催化层的Pt载量 | mPt | mg·cm-2 | 0.2[7] |
| Pt与铂碳催化剂颗粒的质量比 | f | 0.2[7] | |
| Pt的密度 | ρPt | kg·m-3 | 21 400 |
| 碳的密度 | ρC | kg·m-3 | 1 800 |
| 氧气参考浓度 | crefO2 | mol·m-3 | 1.2[5] |
| 阴极电荷转移系数 | αc | 1 | |
| 阳极电荷转移系数 | αa | 0.5 | |
| Nafion的本征质子导率 | κH | S·m-1 | 17[5] |
| Pt/C颗粒的本征电子导率 | σe | S·m-1 | 7.27×104[5] |
| O2在空气中的扩散系数 | DO2 | m2·s-1 | 1.8×10-5[25] |
| 入口处氧气浓度 | c0 | mol·m-3 | 5.2 |
| 电池面电阻 | Rm | Ω·cm2 | 0.24 |
| 注:1 atm=1.013×10-5 Pa。 | |||
由于PEMFC中氢气氧化反应的过电位远低于氧气还原反应的过电位,所以,阳极过电位可以忽略不计。欧姆过电位等于池电流Itot与面电阻的乘积Rm由此,因此电池的输出电压Ecell为:
| ${E_{{\rm{cell}}}} = {E_{\rm{r}}}-{\eta _{\rm{c}}}-{I_{{\rm{tot}}}}{R_{\rm{m}}}$ | (23) |
可逆电池电动势Er为温度和压力的函数[28],表示为:
| ${E_{\rm{r}}} = {E^\theta }-\frac{{RT}}{{2F}}\ln \frac{{{\rho _{{{\rm{H}}_2}O}}}}{{{\rho _{{{\rm{H}}_2}}}p_{{{\rm{O}}_2}}^{1/2}}}$ | (24) |
基于表 1中的参数以及εN=0.4, mPt=0.35 mg·cm-2,f=0.1和lc=50μm对该CCL模型进行模拟计算,并将模拟结果与Ticianelli的实验数值[29]进行比照,如图 2所示。
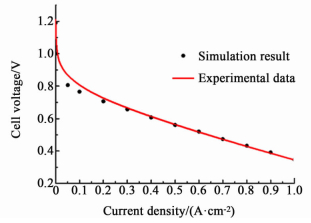
|
| 图 2 模型模拟结果与实验数值的比较 Figure 2 Comparison of simulation result and experimental data |
| |
由图 2可见二者的吻合程度较好,说明此模型能够较好地描述实验结果。
2.1 通过调整铂载量mPt研究催化层厚度变化对PEMFC性能的影响铂载量mPt随CCL厚度lc变化时,二者的对应关系归纳于表 2。催化层内的Pt载量是随着催化层厚度增加而线性增长的,所以催化层内的催化活性面积也是与催化层厚度成正比关系的。
| mPt/(mg·cm-2) | lc/μm |
| 0.002 | 0.1 |
| 0.010 | 0.5 |
| 0.020 | 1.0 |
| 0.040 | 2.0 |
| 0.120 | 6.0 |
| 0.200 | 10.0 |
| 0.300 | 15.0 |
| 注:各催化层的铂碳比f=0.2,比表面积a=22.9 m-1。 | |
催化层厚度不同的PEMFC的功率密度曲线(P-i曲线)示于图 3中。
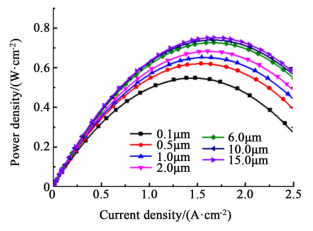
|
| 图 3 不同厚度催化层的功率密度曲线(改变mPt) Figure 3 Power density curves as a function of CCL thickness (changing mPt) |
| |
由图 3可以看出催化层厚15 μm的PEMFC在0~2.5 A·cm-2的电流密度范围内均具有高于其它催化层厚度的电池功率输出,最大值出现在1.5 A·cm-2附近,约为0.75 W·cm-2。随着催化层厚度增加,PEMFC的性能增强,当厚度达到6 μm以上,电池的功率密度输出不再有明显的变化。
为了分析催化层中的物质传递和电化学反应对PEMFC性能的影响,我们将电流密度为1.5 A·cm-2时催化层内的氧气浓度、ORR速率和阴极过电位沿催化层厚度方向的分布示于图 4。图 4中横轴坐标x/lc是比厚度,x/lc=0的位置是M/CCL界面,而x/lc=1是CCL/GDL界面。
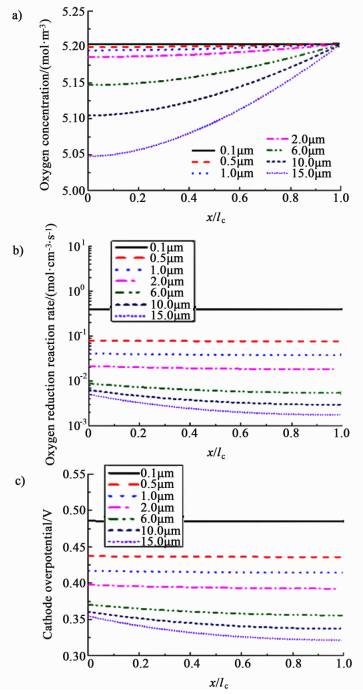
|
| 图 4 不同厚度的催化层在Itot=1.5 A·cm-2时的a)氧气浓度b)ORR和c)阴极过电位的分布曲线(改变mPt) Figure 4 a) Oxygen concentration b) ORR rate and c) cathode overpotential profiles of the CCLs with different thicknesses at Itot=1.5 A·cm-2 (changing mPt) |
| |
由图 4a)可以看出催化层内的氧气浓度分布都比较均匀。在厚度小于2 μm的催化层内,从CCL/GDL界面到M/CCL界面氧气浓度变化极小,而6 μm以上的催化层两界面间的氧气浓度稍有变化,说明催化层内的氧气传质阻力很小,但随催化层厚度的增加,传质阻力增大。催化层内ORR速率分布也很均匀,如图 4b)所示,说明催化层各处的催化剂都被充分利用于电化学反应。6、10和15 μm的催化层内反应速率在M/CCL界面高于CCL/GDL界面,是因为在CCL/GDL界面质子传导路径长,限制了ORR速率。因为催化层被充分利用,越厚的催化层催化剂载量越大,催化活性总面积也越大,所以活化过电位越小,如图 4c)所示。而6、10和15 μm的催化层在M/CCL界面过电位相比于CCL/GDL界面高,是浓差极化影响的结果。总而言之,活化过电位对阴极催化层的过电位影响最大,使得催化层厚度为15 μm的PEMFC在0~2.5 A·cm-2的电流密度范围内具有最高的输出功率。
然而,从催化剂利用率角度分析,最薄的催化层(0.1 μm)的催化剂利用率最高,单位质量Pt的电池功率输出约为275 W·mg-1。这是因为在Pt在碳载铂(Pt/C)颗粒中的质量分数f相同的情况下,单位体积催化层的Pt载量相同。0.1 μm催化层内的平均ORR速率远大于其余催化层,如图 4b)所示,即单位质量催化剂对电化学反应的贡献更多。
2.2 通过调整铂碳比f研究催化层厚度变化对PEMFC性能的影响铂碳比f随催化层厚度变化时,不同厚度的催化层对应的f值列于表 3中。因为f的变化会引起催化剂在碳载体上的分布发生改变,使得催化层的催化活性比表面积a也随之改变,所以催化层内的催化活性总面积随催化层厚度而变化。
| f | lc/ μm | 催化层比表面积a/m-1 | 催化层内的总催化活性面积*/(×10-6cm2) |
| 1.00 | 0.2 | 271.9 | 54.38 |
| 0.89 | 0.5 | 61.1 | 30.56 |
| 0.75 | 1.0 | 30.0 | 29.98 |
| 0.58 | 2.0 | 34.2 | 68.37 |
| 0.30 | 6.0 | 30.5 | 183.25 |
| 0.20 | 10.0 | 22.9 | 229.35 |
| 0.14 | 15.0 | 17.1 | 256.68 |
| 注:各催化层的Pt载量均为0.2 mg·cm-2;*系根据文献[15]计算而得。 | |||
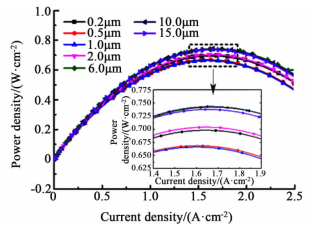
PEMFC的功率密度曲线随催化层厚度的变化示于图 5。
|
| 图 5 不同厚度催化层的功率密度曲线(改变f) Figure 5 Power density curves as a function of CCL thickness (changing f) |
| |
由图 5可以看出,各电池的功率密度输出都很接近,催化层厚6和10 μm的PEMFC几乎同时具备最优的性能。
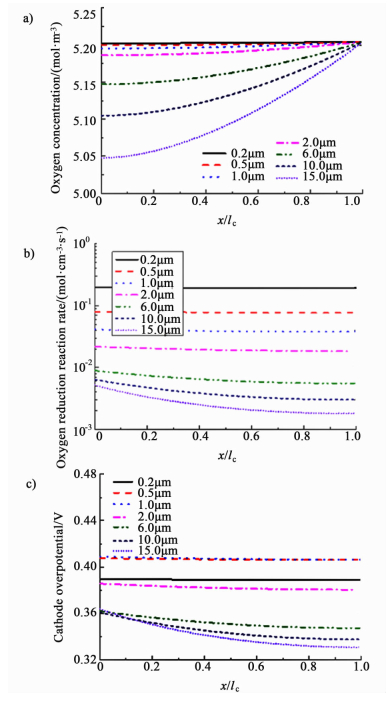
在电流密度为1.5 A·cm-2时催化层内的氧气浓度、ORR速率和阴极过电位沿催化层厚度方向的分布示于图 6。
|
| 图 6 不同厚度的催化层在Itot=1.5 A·cm-2时的a)氧气浓度b)ORR和c)阴极过电位的分布曲线(改变f) Figure 6 a) Oxygen concentration b) ORR rate and c) cathode overpotential profiles of the CCLs with different thicknesses at Itot=1.5 A·cm-2 (changing f) |
| |
由图 6a)我们可以看出催化层内的氧气浓度分布比较均匀,在厚度小于2 μm的催化层内,从CCL/GDL界面到M/CCL界面氧气浓度变化很小,6 μm以上的催化层两界面间的氧气浓度略有变化。这与通过调整mPt改变催化层厚度的研究结果一致。由于在M/CCL界面质子传递路径短、阻力小,而氧气浓度没有大幅降低,所以在6、10和15 μm厚的催化层内,M/CCL界面的ORR速率稍高于CCL/GDL界面[图 6b)]。由图 6c)可以看出,在CCL/GDL界面处的阴极过电位与不同厚度催化层内的催化活性总面积(表 3)直接相关,即活性总面积大则过电位低。其原因是,在此界面氧气的供应充足,过电位的差异主要来自于反比于活性面积的活化过电位。因为氧气传递阻力因素,催化层越厚,浓差过电位就越大,从CCL/GDL界面到M/CCL界面的阴极过电位的增幅就越大[图 6c)]。所以活化过电位与浓差过电位二者共同作用,使得催化层厚度为6和10 μm的电池性能最佳。
从对以上2种变化催化层厚度方式的模拟结果分析得知,最适宜厚度的催化层在全操作电流范围内使得PEMFC具有最高的功率输出。这是因为在低电流密度区,最适宜厚度的催化层具有比薄层更大的催化活性面积,活化过电位更低;而在高电流密度区,最适宜厚度催化层比厚层传质阻力小,浓差极化更弱。在催化层孔隙中无液态水存在的情况下,传质阻力不是决定电池性能的主要因素,所以无论低电流密度还是高电流密度时,活化过电位都对催化层厚度的优化起着主导作用,催化层较厚的PEMFC具有较高的电池功率输出。
3 结论采用一维稳态宏观均相模型首次对不同厚度的PEMFC在全操作电流范围内的功率输出进行了计算和比较。为了保证催化层中各相的体积比不变,催化层厚度采用2种变化方式,一是变位面积催化层内的Pt载量,一是变化Pt在碳载铂(Pt/C)催化剂颗粒中的质量分数。模拟结果表明,变化Pt载量mPt时,催化层越厚则PEMFC的功率输出越高。而催化层越薄,催化剂利用率越高,最高达到225 W·mg-1。当改变Pt/C中Pt质量分数f时,催化层厚度为6~10 μm的PEMFC表现出较其它更优的性能。在本研究中设定的CCL参数范围内,计算所得的最适宜厚度催化层在整个电流密度范围内都使PEMFC有最高的功率输出。研究结果将有助于PEMFC催化层的优化设计。
| [1] | He W, Yi J, Van Nguyen T. Two-Phase flow model of the cathode of PEM fuel cells using interdigitated flow fields[J]. AIChE Journal, 2000, 46(10): 2053–2064. DOI: 10.1002/(ISSN)1547-5905 |
| [2] | Wilson M S, Gottesfeld S. Thin-Film catalyst layers for polymer electrolyte fuel cell electrodes[J]. Journal of Applied Electrochemistry, 1992, 22(1): 1–7. DOI: 10.1007/BF01093004 |
| [3] | Kazim A, Liu H, Forges P. Modelling of performance of PEM fuel cells with conventional and interdigitated flow fields[J]. Journal of Applied Electrochemistry, 1999, 29(12): 1409–1416. DOI: 10.1023/A:1003867012551 |
| [4] | Tiedemann W, Newman J. Maximum effective capacity in an ohmically limited porous electrode[J]. Journal of the Electrochemical Society, 1975, 122(11): 1482–1485. DOI: 10.1149/1.2134046 |
| [5] | Khajeh-Hosseini-Dalasm N, Kermani M J, Moghaddam D G, et al. A parametric study of cathode catalyst layer structural parameters on the performance of a PEM fuel cell[J]. International Journal of Hydrogen Energy, 2010, 35(6): 2417–2427. DOI: 10.1016/j.ijhydene.2009.12.111 |
| [6] | You L, Liu H. A parametric study of the cathode catalyst layer of PEM fuel cells using a pseudo-homogeneous model[J]. International Journal of Hydrogen Energy, 2001, 26(9): 991–999. DOI: 10.1016/S0360-3199(01)00035-0 |
| [7] | Song D, Wang Q, Liu Z, et al. Numerical optimization study of the catalyst layer of PEM fuel cell cathode[J]. Journal of Power Sources, 2004, 126(1): 104–111. |
| [8] | Song D, Wang Q, Liu Z, et al. A method for optimizing distributions of Nafion and Pt in cathode catalyst layers of PEM fuel cells[J]. Electrochimica Acta, 2005, 50(16): 3347–3358. |
| [9] | Ahadian S, Khajeh-Hosseini-Dalasm N, Fushinobu K, et al. An effective computational approach to the parametric study of the cathode catalyst layer of PEM fuel cells[J]. Materials Transactions, 2011, 52(10): 1954–1959. DOI: 10.2320/matertrans.M2011101 |
| [10] | Marr C, Li X. Composition and performance modelling of catalyst layer in a proton exchange membrane fuel cell[J]. Journal of Power Sources, 1999, 77(1): 17–27. DOI: 10.1016/S0378-7753(98)00161-X |
| [11] | Kamarajugadda S, Mazumder S. Numerical investigation of the effect of cathode catalyst layer structure and composition on polymer electrolyte membrane fuel cell performance[J]. Journal of Power Sources, 2008, 183(2): 629–642. DOI: 10.1016/j.jpowsour.2008.05.072 |
| [12] | Yang T, Cheng C, Su A, et al. Numerical analysis of the manipulated high performance catalyst layer design for polymer electrolyte membrane fuel cell[J]. International Journal of Energy Research, 2014, 38(15): 1937–1948. DOI: 10.1002/er.v38.15 |
| [13] | Hu G, Li G, Zheng Y, et al. Optimization and parametric analysis of PEMFC based on an agglomerate model for catalyst layer[J]. Journal of the Energy Institute, 2014, 87(2): 163–174. DOI: 10.1016/j.joei.2014.03.004 |
| [14] | Khajeh-Hosseini-Dalasm N, Fesanghary M, Fushinobu K, et al. A study of the agglomerate catalyst layer for the cathode side of a proton exchange membrane fuel cell: Modeling and optimization[J]. Electrochimica Acta, 2012, 60: 55–65. DOI: 10.1016/j.electacta.2011.10.099 |
| [15] | Secanell M, Karan K, Suleman A, et al. Multi-Variable optimization of PEMFC cathodes using an agglomerate model[J]. Electrochimica Acta, 2007, 52(22): 6318–6337. DOI: 10.1016/j.electacta.2007.04.028 |
| [16] | Secanell M, Songprakorp R, Djilali N, et al. Optimization of a proton exchange membrane fuel cell membrane electrode assembly[J]. Structural and Multidisciplinary Optimization, 2010, 40(1/6): 563–583. |
| [17] | El Hannach M, Pauchet J, Prat M. Pore network modeling: Application to multiphase transport inside the cathode catalyst layer of proton exchange membrane fuel cell[J]. Electrochimica Acta, 2011, 56(28): 10796–10808. DOI: 10.1016/j.electacta.2011.05.060 |
| [18] | El Hannach M, Prat M, Pauchet J. Pore network model of the cathode catalyst layer of proton exchange membrane fuel cells: Analysis of water management and electrical performance[J]. International Journal of Hydrogen Energy, 2012, 37(24): 18996–19006. DOI: 10.1016/j.ijhydene.2012.09.139 |
| [19] | Wu R, Liao Q, Zhu X, et al. Pore network modeling of cathode catalyst layer of proton exchange membrane fuel cell[J]. International Journal of Hydrogen Energy, 2012, 37(15): 11255–11267. DOI: 10.1016/j.ijhydene.2012.04.036 |
| [20] | Wei Z, Ran H, Liu X, et al. Numerical analysis of Pt utilization in PEMFC catalyst layer using random cluster model[J]. Electrochimica Acta, 2006, 51(15): 3091–3096. DOI: 10.1016/j.electacta.2005.08.048 |
| [21] | Mukherjee P P, Wang C. Stochastic microstructure reconstruction and direct numerical simulation of the PEFC catalyst layer[J]. Journal of the Electrochemical Society, 2006, 153(5): A840–A849. DOI: 10.1149/1.2179303 |
| [22] | Wang G, Mukherjee P P, Wang C. Optimization of polymer electrolyte fuel cell cathode catalyst layers via direct numerical simulation modeling[J]. Electrochimica Acta, 2007, 52(22): 6367–6377. DOI: 10.1016/j.electacta.2007.04.073 |
| [23] | 曹鹏贞. PEMFC催化层的Monte Carlo模拟[D]. 天津: 天津大学, 2007 Cao Pengzhen. The Monte Carlo simulation on the catalyst layer of PEMFC[D]. Tianjin: Tianjin University, 2007(in Chinese) |
| [24] | 张洁婧. PEMFC电极微观结构模拟[D]. 天津: 天津大学, 2011 Zhang Jiejing. Simulations of the PEMFC electrode microstructure[D]. Tianjin: Tianjin University, 2011(in Chinese) |
| [25] | 陈秋香. 聚合物膜燃料电池催化层微观模拟研究[D]. 天津: 天津大学, 2013 Chen Qiuxiang. A study on the macro-modeling of catalyst layer in PEM fuel cell[D]. Tianjin: Tianjin University, 2013(in Chinese) |
| [26] | Robert E, Tobias C W. On the conductivity of dispersions[J]. Journal of The Electrochemical Society, 1959, 106(9): 827–833. DOI: 10.1149/1.2427505 |
| [27] | Parthasarathy A, Srinivasan S, Appleby A J, et al. Temperature dependence of the electrode kinetics of oxygen reduction at the platinum/Nafion © interface -A microelectrode investigation[J]. Journal of the Electrochemical Society, 1992, 139(9): 2530–2537. DOI: 10.1149/1.2221258 |
| [28] | Shabgard H R. Investigation and analysis of the condensation phenomena in the cathode electrode of PEM fuel cells[D]. MSc thesis: Amirkabir University of Technology (Tehran Polytechnic), Iran, 2006 |
| [29] | Ticianelli E A, Derouin C R, Redondo A, et al. Methods to advance technology of proton exchange membrane fuel cells[J]. Journal of the Electrochemical Society, 1988, 135(9): 2209–2214. DOI: 10.1149/1.2096240 |
| [30] | Pourmahmoud N, Rezazadeh S, Mirzaee I, et al. Three-Dimensional numerical analysis of proton exchange membrane fuel cell[J]. Journal of Mechanical Science and Technology, 2011, 25(10): 2665–2673. DOI: 10.1007/s12206-011-0743-y |
 2017, Vol. 34
2017, Vol. 34





