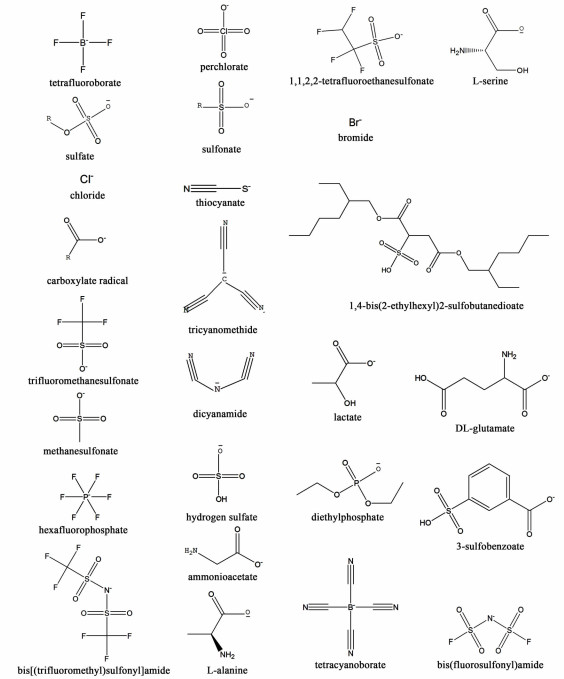
离子液体由有机阳离子和无机或者有机阴离子组成,在100 ℃(大多数在常温下)呈液态[1]。目前,常见的阳离子为:N, N-二烷基咪唑离子、N-烷基吡啶离子、吡咯离子、季铵离子和季鏻阳离子。阴离子的种类很多,常见的主要有:醋酸盐、四氟硼酸盐、六氟磷酸盐和硫酸盐等。离子液体具有几乎可以忽略的饱和蒸汽压、低熔点、低毒性、高密度和良好的溶解性等优点,尤其是离子液体的可设计性,即通过组合不同的阴、阳离子和支链,“按需定制”离子液体,吸引了很多研究者的注意[2-4]。而想要设计出具有特定性质的离子液体,必须先要获得离子液体的物性数据,通过结构与其性质的关系,进而得到合适的结构。
对于研究者来说,测量如此庞大物系的物理化学性质是一项耗时耗力的工作,所以开发估算离子液体性质的计算方法是很必要的。定量结构-性质关系(QSPR)是常用的定量地研究物质结构和其性质关系的方法,关于离子液体的QSPR研究已经涉及到了黏度、密度、无限稀释活度系数和表面张力等方面,而对于光学性质方面的研究较少[5-9]。
折射率是表征物质光学性能的重要参数,通过研究离子液体的折射率可以了解其光学性能、确定其纯度、计算混合物的浓度,而且,折射率与其它性质,如密度、表面张力以及介电常数是相关的。因此,预测并设计出所需要的折射率的离子液体对于开发新的光学材料等具有重要的意义。
目前,对于预测离子液体折射率(nD)的报道较少。Gardas和Coutinho[10]分析了24种咪唑类的离子液体,得到了含有10个基团参数的基团贡献模型,其总的相对偏差仅为0.18%,但该模型没能预测其它类型的离子液体,具有很大的局限性。Soriano等[11]和Freire等[12]使用了相同的方法,也仅仅预测了咪唑类离子液体的折射率。Ramjugernath[13]分析了97种离子液体,包含了50种阳离子和33种阴离子,得到了含有17个基团参数的基团贡献模型,但是基团组合不够灵活,不能为离子液体的设计提供方便。本论文中,搜集了115种离子液体在不同温度下的1 161个折射率数据,运用基团贡献法,得到了39个基团参数的模型,计算值与文献值的平均相对偏差为0.452%,而且基团之间组合灵活,为离子液体的结构设计提供便利。
1 计算部分 1.1 实验数据的选取选用的实验数据取自离子液体数据库(NIST),共115种离子液体(可在本刊网站下载)。其中,阳离子有5类:季铵阳离子、季鏻阳离子、咪唑阳离子、吡啶阳离子和吡咯阳离子,阴离子有26类,详见表 1。
将115种离子液体的结构按照特定的方式进行拆分,然后归类,共得到39个基团,见表 2。
| 基团 | ai | bi | ||
| 阳离子 | 主基团 | Im | 0.843127463 | 0.071220109 |
| Py | 0.869444478 | 0.071213700 | ||
| Pyr | 0.830831697 | 0.071234606 | ||
| N | 0.144353176 | -3.030414080 | ||
| P | 0.199640356 | -3.030507726 | ||
| R1 | CH3— | 0.688671333 | -0.071780609 | |
| —CH2— | 0.000869369 | -2.921334746×10-6 | ||
| C6H5— | 0.755646445 | -0.071786486 | ||
| —OH | 0.701384467 | -0.071773111 | ||
| —CN | 0.741694924 | -0.071756862 | ||
| R2 | CH3— | 0.001457050 | -2.230015429×10-6 | |
| —CH2— | -0.003137008 | 4.011014730×10-6 | ||
| H | -0.000307144 | -4.652805482×10-5 | ||
| R3 | CH3— | 0.343993522 | 48.240948329 | |
| —CH2— | -0.014144141 | 2.252574584×10-5 | ||
| R4 | CH3— | 0.343993538 | -45.139312773 | |
| —CH2— | 0.004256789 | -8.502479091×10-6 | ||
| 阴离子 | CH3— | 0.077508562 | 0.000323780 | |
| SO2 | -0.019017500 | -5.800392392×10-6 | ||
| O | -0.013083864 | -1.360144097×10-5 | ||
| Cl | 0.042012219 | 0.000310375 | ||
| B | -0.194239199 | -0.000932244 | ||
| F | 0.039373716 | 0.000314057 | ||
| COO | -0.040703800 | -6.076985565×10-5 | ||
| H | 0.095496678 | 0.000463450 | ||
| N | -0.040102446 | -0.000336241 | ||
| C | -0.091449390 | -0.000625320 | ||
| C6H4— | 0.035867790 | -5.894469980×10-6 | ||
| S | 0.048340405 | -2.756048953×10-5 | ||
| —CH2— | -0.002591669 | -1.460933106×10-6 | ||
| —CN | 0.049754768 | 0.000301733 | ||
| P | -0.273844001 | -0.001581029 | ||
| NH2 | 0.104471285 | 0.000281311 | ||
| CH | -0.059885029 | -0.000298234 | ||
| OH | 0.053523162 | 0.000365177 | ||
| PO | -0.071619441 | -0.000364562 | ||
| Br | 0.027350602 | 0.000290818 | ||
| C6H5— | 0.061112489 | 0.000297045 | ||
| ClO3 | 0.030350386 | 0.000314309 | ||
如表 2所示,基团划分考虑了阳离子主体部分不同取代基对离子液体折射率的影响,将阳离子划分成主基团、R1、R2、R3和R4 5个部分,其中,主基团是阳离子的中心结构,R1、R2、R3和R4分别为支链结构,依次表示第1、2、3和4个支链,目前搜集到的离子液体,最多含有4个支链。对于阳离子含多个支链的离子液体,支链按照其复杂程度排序。
首先是含有烃基以外的官能团的支链,其次是链长较长或者结构较复杂的支链,例如同时含苄基与乙基2个支链的阳离子,苄基比乙基复杂,因此,该阳离子的支链划分为:1个R1即C7H7,1个R2即C2H5,其中,R1又分为C6H5和CH2,R2又分为1个CH3和1个CH2。2个部分中CH2的贡献值是不同的,这样划分基团虽然增加了复杂性,但是估算精度会有所提高。
为了更加清晰地说明基团的分类方法,以三乙基甲基四氟硼酸铵和1-苄基-3甲基咪唑氯盐为例。前者的阴离子可以划分为1个B和4个F, 阳离子中包含1个主基团:N,1个R1:乙基,1个R2:乙基,1个R3:乙基,1个R4:甲基,其中R1,R2,R3又分别划分为1个CH3和1个CH2。因此,阳离子包含1个主基团:N,R1中的1个CH3和1个CH2,R2中的1个CH3和1个CH2,R3中的1个CH3和1个CH2以及R4中的1个CH3。后者的阴离子为1个Cl,阳离子中包含主基团:咪唑(Im),1个R1:苄基,1个R2:甲基,其中R1又可以划分为:1个C6H5和1个CH2。因此,阳离子包含1个主基团:Im,R1中的1个C6H5和1个CH2,R2中的1个CH3。
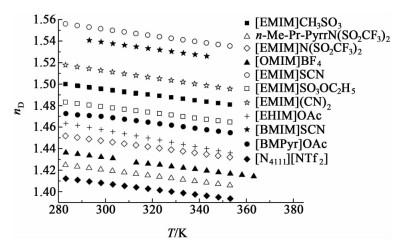
1.3 基团贡献模型的建立考虑到折射率随温度变化的关系,首先将搜集到的115种离子液体在不同温度下折射率的变化作图,为了看起来更加清晰,图 1中仅给出了11种离子液体折射率随温度的变化,剩余的104种离子液体具有同样的变化趋势。
|
| 图 1 离子液体的折射率随温度的变化 Figure 1 The refractive indices of ionic liquids changing with temperature |
| |
由图 1可以看出,离子液体折射率随着温度的变化呈线性关系,且都随着温度的升高有所下降。然后,根据方程1分别对115种离子液体的折射率值进行线性拟合,得到的相关系数都大于0.99。
| $ {n_{\text{D}}}=A + BT/K $ | (1) |
其中,A是离子液体在0 K下的折射率,B是折射率随温度变化的系数。根据Gardas[10]提出的基团贡献方法,A和B可以表示为:
| $ A=\sum\limits_{i=1}^k {{n_i}{a_i}} $ | (2) |
| $ B=\sum\limits_{i=1}^k {{n_i}{b_i}} $ | (3) |
其中,k为不同基团的总数,值为39;ni为基团i的个数;ai,bi分别为基团i对参数A,B的贡献值。
将115种离子液体的1 161个折射率值用上述模型进行回归,得到各个基团的贡献值见表 2。
2 结果与讨论 2.1 标准差和相对偏差的计算为说明此方法的回归效果,用式(4) 计算了估算的标准差,式中n表示数据点数1 161。结果显示参与估算的折射率数据的标准方差为0.00897。
| $ s=\sqrt {\frac{{\sum {{{({n_{{{\text{D}}_{{\text{cal}}}}}} - {n_{{{\text{D}}_{{\text{lit}}}}}})}^2}} }}{{n - 1}}} $ | (4) |
用回归得到的基团的贡献值,计算参与估算的1 161个折射率值,用式(5) 计算文献值与计算值的相对偏差(RD),进而可以求出计算的平均相对偏差(ARD)为0.452%。具体的相对偏差的分布情况见图 2。
| $ {\text{RD=}}\frac{{|{n_{{{\text{D}}_{{\text{cal}}}}}} - {n_{{{\text{D}}_{{\text{lit}}}}}}|}}{{{n_{{{\text{D}}_{{\text{lit}}}}}}}} \times 100\% $ | (5) |

|
| 图 2 离子液体折射率计算值与文献值的相对偏差的分布比例 Figure 2 The distribution of relative deviations between calculated and the literature values |
| |
由图 2可以看出,97.93%的数据点的相对偏差小于2%,说明该方法是比较精确的。另外有2.07%数据点的相对偏差大于2%,这部分数据是由Ziyada[14-16]测量的[CNC2Oim]Cl(RD=2.7346%)、[CNC2Oim]TFMS(RD=2.068%)和[CNC2Him]TFMS(RD=2.032%),测得数据的不确定度相对较小,分别是0.00057、00006和0.00081,所以应该不是数据测量不准确,而有可能是因为离子液体中杂质含量比较高:含水量分别为0.0259%、0.0179%和0.0243%,另还含有一定的Br杂质。
2.2 基团贡献法验证为了更好的检验估算方法的准确性,利用该方法估算未参与回归的离子液体[EM2N(CH2)2OH][ESO4][17]和[P666(14)][Deca][18]的折射率,结果见表 3。得到的2种具有代表性的离子液体折射率的估算值与文献实验值的相对偏差分别为0.520%和0.284%,平均相对偏差为0.331%,说明该方法是可靠的。但是由于所搜集的离子液体的阳离子中很少具有3个支链,所以该方法对于估算阳离子具有3个支链的离子液体的折射率有一定的局限性。
| 离子液体 | 部分 | 基团 | 基团数量 | T/K | nDlit | nDcal | RD | ARD |
 |
主基团 | N | 1 | 298.15 | 1.47303[17] | 1.48069 | 0.520% | 0.520% |
| R1 | CH2 | 2 | ||||||
| OH | 1 | |||||||
 |
R2 | CH3 | 1 | |||||
| CH2 | 1 | |||||||
| R3 | CH3 | 1 | ||||||
| R4 | CH3 | 1 | ||||||
| 阴离子 | CH3 | 1 | ||||||
| CH2 | 1 | |||||||
| SO2 | 1 | |||||||
| O | 2 | |||||||
 |
主基团 | P | 1 | 293.15 | 1.47413[18] | 1.46943 | 0.319% | 0.284% |
| R1 | CH3 | 1 | 298.15 | 1.47242[18] | 1.46784 | 0.311% | ||
| CH2 | 13 | 313.15 | 1.46722[18] | 1.46308 | 0.282% | |||
| R2 | CH3 | 1 | 333.15 | 1.46002[18] | 1.45673 | 0.225% | ||
| CH2 | 5 | |||||||
 |
R3 | CH3 | 1 | |||||
| CH2 | 5 | |||||||
| R4 | CH3 | 1 | ||||||
| CH2 | 5 | |||||||
| CH3 | 1 | |||||||
| 阴离子 | CH2 | 8 | ||||||
| COO | 1 |
Freire等[12]之前的文献中仅仅提出了预测咪唑类离子液体折射率的基团贡献法;Ramjugernath[13]的文中分析了97种离子液体,得到了17个基团参数模型;而本论文中搜集了115种离子液体,通过新的基团划分方法得的39个基团参数更能灵活的组合成新型的离子液体,而且该模型预测的离子液体折射率的平均相对偏差仅为0.331%,小于Ramjugernath[13]提出的17参数模型的平均相对偏差为0.45%,说明该方法更为灵活、准确。
3 结论提出一种新型的基团分类方法,通过回归115种离子液体的1 161个折射率数据点,建立了1个含有39个基团参数的基团贡献模型来预测离子液体的折射率,回归标准差和相对偏差的值分别为0.00897和0.452%。使用该方法计算了未参与回归的2种离子液体的5个数据点,得到的相对偏差分别是0.520%和0.284%,说明该基团贡献模型和该基团分类方法是准确、可靠的。
| [1] |
蒋鹏忠. 离子液体的应用与发展前景[J].
科教文汇(中旬刊), 2008(3): 195–196.
Jiang Pengzhong. The application and development prospects of ionic liquids[J]. Education Science & Culture Magazine, 2008(3): 195–196. |
| [2] | Brennecke J F, Maginn E J. Ionic liquids: Innovative fluids for chemical processing[J]. AIChE Journal, 2001, 47(11): 2 384–2 389. DOI: 10.1002/(ISSN)1547-5905 |
| [3] |
彭艳枚, 崔现宝, 张缨, 等. 甲醇-乙酸甲酯-1-丁基-3-甲基咪唑双三氟甲磺酰亚胺盐的等压汽液平衡[J].
化学工业与工程, 2013, 30(6): 27–31.
Peng Yanmei, Cui Xianbao, Zhang Ying, et al. Isobaric vapor-liquid equilibrium for methanol-methyl acetate-1-butyl-3-methyl-imidazoliumbis [(trifluoromethyl) sulfonyl] imide at 101.3 kPa[J]. Chemical Industry and Engineering, 2013, 30(6): 27–31. |
| [4] |
关淑霞, 于海南, 邰永娜. 离子液体的应用进展[J].
化学工业与工程技术, 2011, 32(6): 32–36.
Guan Shuxia, Yu Hainan, Tai Yongna. Application progress of ionic liquids[J]. Chemical Industry and Engineering, 2011, 32(6): 32–36. |
| [5] |
盛卫心, 戎宗明, 英徐根. 基团贡献法分子设计研究的进展[J].
化学工业与工程, 2007, 24(5): 457–465.
Sheng Weixin, Rong Zongming, Ying Xugen. Progress in computer-aided molecular design based on group contribution method[J]. Chemical Industry and Engineering, 2007, 24(5): 457–465. |
| [6] |
文路. 离子液体粘度的QSPR研究[D]. 北京: 北京化工大学, 2011
Wen Lu. QSPR study on the viscosity of ionic liquids[D]. Beijing: Beijing University of Chemical Technology, 2011(in Chinese) |
| [7] | Qiao Y, Ma Y, Huo Y, et al. A group contribution method to estimate the densities of ionic liquids[J]. The Journal of Chemical Thermodynamics, 2010, 42(7): 852–855. DOI: 10.1016/j.jct.2010.02.007 |
| [8] |
李瑞. 离子液体萃取精馏的萃取剂分子设计[D]. 天津: 天津大学, 2012
Li Rui. Molecular design of ionic liquid entrainers for extractive distillation[D]. Tianjin: Tianjin University, 2012(in Chinese) |
| [9] |
马沛生, 李平, 赵兴民, 等. 用基团贡献方法估算20 ℃下表面张力[J].
化工学报, 1994, 45(1): 112–116.
Ma Peisheng, Li Ping, Zhao Xingmin, et al. Estimating surface tensions by a group contribution method when the temperature is less than 20℃[J]. Journal of Chemical Industry and Engineering, 1994, 45(1): 112–116. |
| [10] | Gradas R L, Coutinho J A P. Group contribution methods for the prediction of thermophysical and transport properties of ionic liquids[J]. AIChE Journal, 2009, 55(5): 1 274–1 290. DOI: 10.1002/aic.v55:5 |
| [11] | Soriano A N, Doma Jr B T, Li M. Density and refractive index measurements of 1-ethyl-3-methylimidazolium-based ionic liquids[J]. Journal of the Taiwan Institute of Chemical Engineers, 2010, 41(1): 115–121. DOI: 10.1016/j.jtice.2009.07.002 |
| [12] | Freire M G, Teles A R R, Rocha M A A, et al. Thermophysical characterization of ionic liquids able to dissolve biomass[J]. Journal of Chemical & Engineering Data, 2011, 56(12): 4 813–4 822. |
| [13] | Sattari M, Kamari A, Mohammadi A H, et al. A group contribution method for estimating the refractive indices of ionic liquids[J]. Journal of Molecular Liquids, 2014, 200, Part B: 410–415. |
| [14] | Ziyada A K, Wilfred C D, Murugesan T. Densities, viscosities and refractive indices of 1-alkyl-3-propanenitrile imidazolium chloride ionic liquids[J]. Physics and Chemistry of Liquids, 2011, 50(2): 152–160. |
| [15] | Ziyada A K, Wilfred C D. Effect of temperature and anion on densities, viscosities, and refractive indices of 1-octyl-3-propanenitrile imidazolium-based ionic liquids[J]. Journal of Chemical & Engineering Data, 2014, 59(5): 1 385–1 390. |
| [16] | Ziyada A K, Bustam M A, Wilfred C D, et al. Densities, viscosities, and refractive indices of 1-hexyl-3-propanenitrile imidazolium ionic liquids incorporated with sulfonate-based anions[J]. Journal of Chemical & Engineering Data, 2011, 56(5): 2 343–2 348. |
| [17] | Mahrova M, Vilas M, Domínguez A, et al. Physicochemical characterization of new sulfonate and sulfate ammonium ionic liquids[J]. Journal of Chemical & Engineering Data, 2012, 57(2): 241–248. |
| [18] | Almeida H F D, Lopes-da-Silva J A, Freire M G, et al. Surface tension and refractive index of pure and water-saturated tetradecyltrihexylphosphonium-based ionic liquids[J]. The Journal of Chemical Thermodynamics, 2013, 57(10): 372–379. |
 2017, Vol. 34
2017, Vol. 34