地氯雷他定是治疗过敏性疾病的一线药物[1],具有很强的抗组胺活性,且无心脏毒性、无中枢镇静作用。反式-4-羟基环己基地氯雷他定是地氯雷他定的衍生物,在之前的研究中,Lin Yan等[2]发现它在体内和体外均表现出了很强的抗组胺活性,当给药量仅为地氯雷他定的质量的1%时,就能达到地氯雷他定的药效,此外能够显著的拮抗由组胺引起的痉挛,具有成为抗组胺新药的潜质。其结构如图 1。
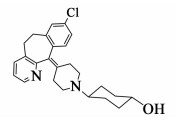
|
| 图 1 反式-4-羟基环己基地氯雷他定结构式 Figure 1 The structure of trans-4-hydroxycyclohexyl desloratadine |
| |
对于药物来说,溶解度往往会直接影响其在生物体内的溶出度,进而影响到药物的生物活性,与剂型、制剂的选择及工艺、处方、质量控制等具有密切的关系。而通过查阅文献我们发现,尚未有文献对其溶解度数据进行报道。因此,测定反式-4-羟基环己基地氯雷他定在不同溶剂中的溶解度就显得非常重要。
本研究采用高效液相色谱法测定了反式-4-羟基环己基地氯雷他定在水、质量分数为10%的甲醇-水、质量分数为20%的甲醇-水、质量分数为10%的乙醇-水和质量分数为20%的乙醇-水中的溶解度,并采用Apelblat方程和λh方程对所得到的溶解度数据进行关联拟合,通过van’t Hoff方程计算了其在不同溶剂中的溶解焓和溶解熵,来理解反式-4-羟基环己基地氯雷他定的溶解过程。
1 实验部分 1.1 实验试剂实验所用反式-4-羟基环乙基地氯雷他定样品为实验室自制,经提纯后,HPLC检测其质量分数达到99%以上,符合溶解度测定要求。所用水为去离子水,且经过两次重蒸。所用溶剂皆为市售。
1.2 实验设备及分析方法溶解度测试所用仪器列于表 1。
| 仪器名称 | 型号 | 生产厂家 |
| 电子分析天平 | AL104 | Mettler Toledo公司 |
| 恒温震荡水浴槽 | Julabo SW23 | 德国Julabo公司 |
| 移液器 | DR720060 | Dragon-Med公司 |
| 高效液相色谱 | Agilent 1100 Series | 美国Agilent公司 |
| 精密温度计 | ±0.1 ℃ | - |
采用Agilent 1100 Series液相色谱仪来分析样品浓度。检测波长为256 nm,色谱柱为C18反相色谱柱(250 mm×4.6 mm I.D.,4 μm,Agilent),流动相为V(甲醇):V(水)=1:4,流速为0.8 mL/min,进样量为5 μL。
1.3 反式-4-羟基环己基地氯雷他定溶解度的测定在测试之前,将反式-4-羟基环乙基地氯雷他定置于真空干燥箱,于60 ℃下干燥14 h以确保除去样品中的全部水分,干燥后的样品置于干燥器中,用时取出。测试时向10 mL塞有玻璃塞的单口烧瓶中加入6 mL左右溶剂和略微过量的样品,保证测试过程中烧瓶中始终存在固体。用四氟带和封口胶密封,以防止溶剂的挥发。将单口瓶置于恒温震荡水浴槽(精确度为±0.02 ℃),在预设温度下以150 r/min振荡频率震荡10 h保证溶解过程达到平衡,静置5 h,待固体全部沉淀后,用移液器小心移取一定量的上层清液。移液器预先加热,以防止固体在取样时析出。将上层清液用对应溶剂稀释若干倍后,用HPLC分析,通过标准曲线得出稀释后的浓度,计算后得到该温度下的饱和浓度。在相同实验条件下,平行测定3次,取所得平均值作为该温度下反式-4-羟基环乙基地氯雷他定的溶解度。
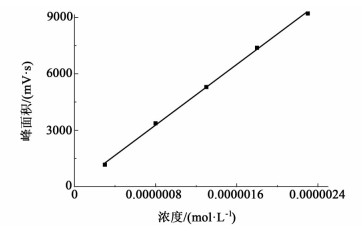
通过配置一系列浓度范围在3.0×10-7~2.3×10-6 mol·mL-1的反式-4-羟基环乙基地氯雷他定标准溶液,绘制峰面积(mV·s)与浓度(mol·mL-1)关系的标准曲线图(见图 2),测试结果表明峰面积与样品浓度呈线性关系,且回归结果良好,相关系数R2=0.999。
|
| 图 2 反式-4-羟基环乙基地氯雷他定的浓度与峰面积关系的标准曲线 Figure 2 Linear relationship between the concentration of trans-4-hydroxycyclohexyl desloratadine and the peak area |
| |
测量了常压下反式-4-羟基环己基地氯雷他定在293.15~323.15 K温度范围内在水、质量分数为10%的甲醇-水、质量分数为20%的甲醇-水、质量分数为10%的乙醇-水和质量分数为20%的乙醇-水中的溶解度,以5 K为1个间隔取实验点。溶解度按公式(1) 计算:
| $ {x^{\exp }}=\frac{{{m_1}/{M_1}}}{{{m_1}/{M_1}+{m_2}/{M_2}+{m_3}/{M_3}}} $ | (1) |
式(1) 中m1,m2和m3分别代表反式-4-羟基环己基地氯雷他定、甲醇或乙醇及水在体系中的质量;M1、M2和M3分别指其相应的摩尔质量;xexp是溶解度的实验测量值。
2.1 溶解度数据反式-4-羟基环己基地氯雷他定在溶剂中的溶解度数据列于表 2,其中xc, Apelb、xc,λh和xc, van分别为溶解度数据的Apelblat方程的拟合值、λh方程和van’t Hoff方程的拟合值。实验值与拟合值的偏差用相对误差(relative deviations,RD)来衡量,按公式(2) 计算。
| $ {\text{RD=}}\frac{{{x^{\exp }} - {x^{\text{c}}}}}{{{x^{\exp }}}} $ | (2) |
| T/K | 105xexp | 105xc, Apelb | 102RD | 105xc,λh | 102RD | 105xc, van | 102RD | |
| water | ||||||||
| 293.15 | 1.5544 | 1.5095 | 2.89 | 1.5416 | 0.82 | 1.5108 | 2.80 | |
| 298.15 | 2.0216 | 2.0036 | 0.89 | 2.0346 | -0.64 | 2.0243 | -0.13 | |
| 303.15 | 2.5569 | 2.6486 | -3.59 | 2.6678 | -4.34 | 2.6862 | -5.06 | |
| 308.15 | 3.6618 | 3.4874 | 4.76 | 3.4788 | 5.00 | 3.5319 | 3.55 | |
| 313.15 | 4.4053 | 4.5743 | -3.84 | 4.5166 | -2.53 | 4.6035 | -4.50 | |
| 318.15 | 5.9892 | 5.9776 | 0.19 | 5.8455 | 2.40 | 5.9505 | 0.65 | |
| 323.15 | 7.8131 | 7.7830 | 0.39 | 7.5525 | 3.34 | 7.6307 | 2.33 | |
| methanol (ω)+water (1-ω) | ||||||||
| ω=10% | 293.15 | 4.8614 | 4.6203 | 4.96 | 4.8338 | 0.57 | 4.7854 | 1.56 |
| 298.15 | 5.9333 | 5.9089 | 0.41 | 5.9696 | -0.61 | 5.9781 | -0.76 | |
| 303.15 | 7.1309 | 7.4401 | -4.34 | 7.3499 | -3.07 | 7.4133 | -3.96 | |
| 308.15 | 9.3967 | 9.2315 | 1.76 | 9.0301 | 3.90 | 9.1292 | 2.85 | |
| 313.15 | 11.291 | 11.297 | -0.05 | 11.082 | 1.85 | 11.168 | 1.09 | |
| 318.15 | 13.426 | 13.644 | -1.62 | 13.600 | -1.30 | 13.575 | -1.11 | |
| 323.15 | 16.433 | 16.276 | 0.96 | 16.713 | -1.70 | 16.402 | 0.19 | |
| ω=20% | 293.15 | 8.6639 | 8.9759 | -3.60 | 8.7402 | -0.88 | 8.7098 | -0.53 |
| 298.15 | 10.981 | 11.040 | -0.54 | 10.878 | 0.94 | 10.924 | 0.52 | |
| 303.15 | 13.733 | 13.569 | 1.19 | 13.491 | 1.76 | 13.599 | 0.98 | |
| 308.15 | 16.634 | 16.663 | -0.17 | 16.690 | -0.34 | 16.809 | -1.05 | |
| 313.15 | 20.431 | 20.446 | -0.07 | 20.616 | -0.91 | 20.637 | -1.01 | |
| 318.15 | 25.638 | 25.064 | 2.24 | 25.456 | 0.71 | 25.174 | 1.81 | |
| 323.15 | 30.293 | 30.696 | -1.33 | 31.465 | -3.87 | 30.520 | -0.75 | |
| ethanol (ω)+water (1-ω) | ||||||||
| ω=10% | 293.15 | 11.117 | 11.885 | -6.91 | 11.123 | -0.05 | 11.117 | 0.00 |
| 298.15 | 14.564 | 15.159 | -4.09 | 14.812 | -1.70 | 14.866 | -2.07 | |
| 303.15 | 20.493 | 19.484 | 4.92 | 19.590 | 4.41 | 19.690 | 3.92 | |
| 308.15 | 25.775 | 25.220 | 2.15 | 25.754 | 0.08 | 25.842 | -0.26 | |
| 313.15 | 33.527 | 32.856 | 2.00 | 33.694 | -0.50 | 33.623 | -0.29 | |
| 318.15 | 41.588 | 43.058 | -3.53 | 43.924 | -5.62 | 43.387 | -4.33 | |
| 323.15 | 57.190 | 56.736 | 0.79 | 57.137 | 0.09 | 55.547 | 2.87 | |
| ω=20% | 293.15 | 29.605 | 28.678 | 3.13 | 29.893 | -0.97 | 29.889 | -0.96 |
| 298.15 | 41.987 | 40.508 | 3.52 | 40.953 | 2.46 | 41.074 | 2.17 | |
| 303.15 | 55.748 | 56.082 | -0.60 | 55.638 | 0.20 | 55.856 | -0.19 | |
| 308.15 | 74.742 | 76.185 | -1.93 | 75.038 | -0.40 | 75.203 | -0.62 | |
| 313.15 | 95.547 | 101.66 | -6.40 | 100.57 | -5.26 | 100.294 | -4.97 | |
| 318.15 | 142.27 | 133.36 | 6.26 | 134.13 | 5.72 | 132.552 | 6.83 | |
| 323.15 | 169.13 | 172.18 | -1.80 | 178.25 | -5.39 | 173.678 | -2.69 | |
式(2) 中xc为溶解度数据的计算值。
反式-4-羟基环己基地氯雷他定溶解度随温度变化的关系如图 3所示。

|
| 图 3 反式-4-羟基环己基地氯雷他定在不同温度下在水和二元溶液中的溶解度数据 Figure 3 Experimental mole fraction solubility (x) of trans-4-hydroxycyclohexyldesloratadine in water and binary solvent at different temperatures |
| |
由图 3可知在实验温度范围内,反式-4-羟基环己基地氯雷他定的溶解度在所有溶剂中均随着温度的升高而增加,在不同组成的溶剂中其溶解度随温度的增长速率也不相同,且不同组成的溶剂对其溶解能力也不同。可以看出对反式-4-羟基环己基地氯雷他定的溶解能力是按照水、甲醇、乙醇的顺序递增的,而三者的极性顺序大小如下:水>甲醇>乙醇,所以我们可以在一定程度上认为反式-4-羟基环己基地氯雷他定的溶解度随着溶剂极性的升高而降低。当改变溶液的组成时,发现随着水中甲醇或乙醇质量分数的增加,反式-4-羟基环己基地氯雷他定的溶解度显著升高,进一步印证了我们的猜想。
从结构上来看反式-4-羟基环己基地氯雷他定虽然带有1个羟基使其具有一定的亲水性和极性,但三环酮结构的存在还是使分子整体上来讲具有较强的疏水性及较弱的极性,所以根据相似相溶的原理,溶解度随着溶液极性的降低而升高。同时由于分子中含有羟基,使得反式-4-羟基环己基地氯雷他定分子会与溶剂分子形成氢键,在一定程度上有利于其在极性溶剂中的溶解,这也是虽然其分子整体上具有较强的疏水性,但在水-甲醇和水-乙醇混合溶液中仍具有一定的溶解性的原因。
2.2 溶解度数据关联与热力学计算将实验中反式-4-羟基环己基地氯雷他定在不同组成溶剂中溶解度随着温度变化趋势分别用Apelblat方程、λh方程和van’t Hoff方程进行关联拟合,以验证所得实验数据的稳定性。溶解度数据的关联效果用均方根偏差(root-mean-square deviation,RMSD)来衡量,其定义式如下:
| $ {\text{RMSD=}}{\left[{\frac{1}{N}\sum\limits_{i=1}^N {{{(\frac{{{x^{\exp }}-{x^{\text{c}}}}}{{{x^{\exp }}}})}^2}} } \right]^{\frac{1}{2}}} $ | (3) |
式(3) 中N表示实验数据点的个数,xexp和xc为溶解度数据的实验值和拟合值。
2.2.1 Apelblat方程Apelblat方程起源于Williamson方程[3-4],最初由Apelblat提出并用于分析温度与溶解度之间的依赖关系。Apelblat方程为一半经验方程[5],其形式简单,方程中仅有3个经验常数,因此常用于溶解度数据的关联拟合、内插和圆滑,并可在小范围内做简单的外推计算,其具体形式如式(4)。
| $ \ln {x_1}=A+\frac{B}{T}+C\ln T $ | (4) |
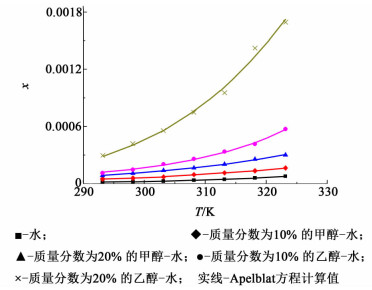
式(4) 中A、B、C为Apelblat方程的经验参数。其中A和B代表了活度系数在溶液中的偏离理想状态的程度,C代表了温度对熔化焓的影响[6-7]。本研究利用Apelblat方程对溶解度数据进行关联拟合,以溶解度x1对温度T作图,结果如图 4所示。
|
| 图 4 反式-4-羟基环己基地氯雷他定溶解度数对温度的Apelblat方程拟合图 Figure 4 Experimental and correlated mole fraction solubility (x) of trans-4-hydroxycyclohexyl desloratadine in water and binary solvent at different temperatures |
| |
通过实验数据回归计算出了Apelblat方程3个经验参数的值,结果列于表 3,Apelblat方程对溶解度数据关联拟合的相关性系数R2及均方根偏差RMSD也列于表 3。
| ω/% | A | B | C | R2 | 105RMSD |
| water | |||||
| -121.978 | 697.113 | 19.100 | 0.998 | 0.10 | |
| methanol+water | |||||
| 10 | 184.707 | -12 256.225 | -26.912 | 0.998 | 0.19 |
| 20 | -144.057 | 2 882.189 | 21.988 | 0.998 | 0.30 |
| ethanol+water | |||||
| 10 | -374.049 | 12 519.833 | 56.737 | 0.997 | 0.85 |
| 20 | 222.423 | -15 317.894 | -31.392 | 0.992 | 4.33 |
λh方程由Buchowski等首先提出[8-9],由于具有处理极性体系的能力[10],被广泛用于固液平衡的实验数据关联[11]。文献[12]报道,若将二元混合溶剂视为一元组分处理,用λh方程关联拟合溶解度数据也能得到很高的精度。λh方程形式如下:
| $ \ln \left[{1+\frac{{\lambda (1-{x_1})}}{{{x_1}}}} \right]=\lambda h\left( {\frac{1}{T} - \frac{1}{{{T_m}}}} \right) $ | (5) |
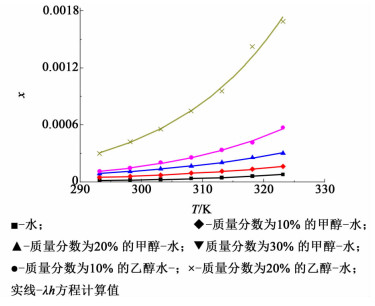
式(5) 中λ、h为λh方程的经验参数。λh方程中只有2个参数,在用于固液平衡计算时具有一定的优势。本研究利用λh方程对溶解度数据进行关联拟合,以溶解度x1对温度T作图,结果如图 5所示。
|
| 图 5 反式-4-羟基环己基地氯雷他定溶解度数对温度的λh方程拟合图 Figure 5 Experimental and correlated mole fraction solubility (x) of trans-4-hydroxycyclohexyl desloratadine in water and binary solvent at different temperatures |
| |
通过实验数据回归计算了λh方程中λ和h的值,λ和h能从微观上反映缔合体系的非理想性[13-14],结果列于表 4,λh方程对溶解度数据关联拟合的相关性系数R2及均方根偏差RMSD也列于表 4。
| ω/% | 103λ | h | R2 | 105RMSD |
| water | ||||
| 0.548 | 7 827 940.134 | 0.998 | 0.10 | |
| methanol+water | ||||
| 10 | 0.555 | 5 899 106.886 | 0.997 | 0.20 |
| 20 | 1.080 | 3 105 777.582 | 0.998 | 0.31 |
| ethanol+water | ||||
| 10 | 4.280 | 1 118 610.142 | 0.997 | 0.85 |
| 20 | 16.293 | 319 199.439 | 0.991 | 4.62 |
根据文献报道[15-16]可知,在不大的温度范围内,溶质在溶剂中的溶解度与温度的关系应当符合van’t Hoff方程,即式(6)。
| $ \ln {x_1}= - \frac{{\Delta {H_{\text{F}}}}}{{RT}}+\frac{{\Delta {S_{\text{F}}}}}{R} $ | (6) |
式(6) 中ΔHF和ΔSF分别代表了物质的摩尔熔化焓和摩尔熔化熵。理想溶液的溶解过程通常被描述为以下过程:溶质从体系温度T被加热到其熔点温度变为液体,然后液相状态的溶质再同溶剂混合,形成溶液[17]。但由于实际溶液的非理想性,溶剂效应的影响必须被考虑进去。依据文献[18],ΔHF和ΔSF应被物质的摩尔溶解焓和摩尔溶解熵ΔHd和ΔSd所替代,因此式(6) 转化为:
| $ \ln {x_1}= - \frac{{\Delta {H_{\text{d}}}}}{{RT}}+\frac{{\Delta {S_{\text{d}}}}}{R} $ | (7) |
通过对反式-4-羟基环己基地氯雷他定在不同组成溶剂中溶解度的对数ln(x1)对1/T作图,来考察所得溶解度数据是否符合van’t Hoff方程,结果如图 6所示。ln(x1)与1/T呈良好的线性关系,这表明van’t Hoff方程可用来描述反式-4-羟基环己基地氯雷他定在所选溶剂中的溶解过程。曲线关联的相关性系数R2及均方根偏差RMSD列于表 5。

|
| 图 6 反式-4-羟基环己基地氯雷他定溶解度数对温度的van’t Hoff方程拟合图 Figure 6 Experimental mole fraction and van't Hoff plot of logarithm mole fraction solubility of trans-4-hydroxycyclohexyl desloratadine in water and binary solvent at different temperatures |
| |
| ω/% | ΔHd | ΔSd | R2 | 105RMSD |
| water | ||||
| 42 520.377 | 52.754 | 0.996 | 0.13 | |
| methanol+water | ||||
| 10 | 32 341.385 | 27.617 | 0.997 | 0.17 |
| 20 | 32 921.859 | 34.576 | 0.999 | 0.23 |
| ethanol+water | ||||
| 10 | 42 238.066 | 68.385 | 0.997 | 0.98 |
| 20 | 46 200.527 | 90.125 | 0.996 | 4.45 |
同时我们利用van’t Hoff方程计算了不同组成溶剂中反式-4-羟基环己基地氯雷他定溶解过程的ΔHd和ΔSd,结果列于表 5。
由表 5可以看出反式-4-羟基环己基地氯雷他定在所有溶剂中溶解过程的ΔHd和ΔSd均大于0,这定在所有溶剂中溶解过程的ΔHd和ΔSd均大于0,这表明其溶解为一吸热和不可逆熵增过程。
3 结论1) 采用高效液相色谱法测定了293.15~323.15 K温度范围内反式-4-羟基环己基地氯雷他定在水、质量分数为10%的甲醇-水、质量分数为20%的甲醇-水、质量分数为10%的乙醇-水和质量分数为20%的乙醇-水中的溶解度。
2) 溶解度测定结果表明,反式-4-羟基环己基地氯雷他定溶解度随着温度的升高和溶液极性的降低而升高。
3) 采用van’t Hoff方程、Apelblat方程和λh方程对实验所得溶解度数据进行了关联拟合,并计算了相关的经验参数。三者均得到了较好的拟合效果,其中Apelblat方程的拟合结果与实验数据具有更好的一致性。
4) 通过van’t Hoff方程计算了其溶解过程的溶解熵和溶解焓,发现反式-4-羟基环己基地氯雷他定在实验所选溶剂中的溶解过程均为吸热、熵增过程。
| [1] | Geha R S, Meltzer E O. Desloratadine: A new, nonsedating, oral antihistamine[J]. J Allergy Clin Immunol, 2001, 107(4): 751–762. DOI: 10.1067/mai.2001.114239 |
| [2] | Lin Y, Wang Y, Sima L F, et al. Design, synthesis and biological activity evaluation of desloratadine analogues as H1 receptor antagonists[J]. Bioorganic & Medicinal Chemistry, 2013, 21(14): 4 178–4 185. |
| [3] | Apelblat A, Manzurola E. Solubilities of L-glutamic acid, 3-nitrobenzoic acid, p-toluic acid, calcium-L-acetate, calcium gluconate, magnesium-DL-aspartate, and magnesium-L-lactate in water[J]. J Chem Thermodyn, 2002, 34: 1 127–1 136. DOI: 10.1006/jcht.2002.0975 |
| [4] | Williamson A T. The exact calculation of heats of solution from solubility data[J]. Trans Faraday Soc, 1944, 40: 421–436. DOI: 10.1039/tf9444000421 |
| [5] | Zhao H, Xu H, Yang Z, et al. Solubility of 3, 4-dichloronitrobenzene in methanol, ethanol, and liquid mixtures (methanol+water, ethanol+water): Experimental measurement and thermodynamic modeling[J]. J Chem Eng Data, 2013, 58: 3 061–3 068. DOI: 10.1021/je400507u |
| [6] | Heryanto R, Hasan M, Abdullah E C, et al. Solubility of stearic acid in various organic solvents and its prediction using non-ideal solution models[J]. Sci Asia, 2007, 33: 469–472. DOI: 10.2306/scienceasia1513-1874.2007.33.469 |
| [7] | Liu B, Gong J, Wang J, et al. Solubility of potassium calvulanate in ethanol, 1-propanol, 1-butanol, 2-propanol, and 2-methyl-1-propanol between 273 K and 305 K[J]. J Chem Eng Data, 2005, 50: 1 684–1 686. DOI: 10.1021/je050145r |
| [8] | Buchowski H, Ksiazczak A, Pietrzyk S. Solvent activity along a saturation line and solubility of hydrogen-bonding solids[J]. J Phys Chem, 1980, 84: 975–979. DOI: 10.1021/j100446a008 |
| [9] | Buchowski H, Khiat A. Solubility of solids in liquids: One-Parameter solubility equation[J]. Fluid Phase Equilib, 1986, 25: 273–278. DOI: 10.1016/0378-3812(86)80003-6 |
| [10] | Sunsandee N, Hronec M, Stolcova, et al. Thermodynamics of the solubility of 4-acetylbenzoic acid in different solvents from 303.15 to 473.15 K[J]. J Mol Liq, 2013, 180: 252–259. DOI: 10.1016/j.molliq.2013.01.023 |
| [11] | Zhou L, Zhang P, Yang G, et al. Solubility of chrysin in ethanol and water mixtures[J]. Journal of Chemical & Engineering Data, 2014, 59(7): 2 215–2 220. |
| [12] | Domanska U. Vapour-Liquid-Solid equilibrium of eicosanoic acid in one-and two-component solvents[J]. Fluid Phase Equilibria, 1986, 26(2): 201–220. DOI: 10.1016/0378-3812(86)90006-3 |
| [13] | Chen J, Zeng Z, Xue W, et al. Determination and correlation of solubility of decahydropyrazino [2, 3-b] pyrazine in methanol, ethanol, and 2-propanol[J]. Ind Eng Chem Res, 2011, 50(20): 11 755–11 762. DOI: 10.1021/ie2012714 |
| [14] | Li D, Liu J, Liu D, et al. Solubilities of terephthalaldehydic, p-toluic, benzoic, terephthalic and isophthalic acids in N, N-dimethylformamide from 294.75 K to 370.45 K[J]. Fluid Phase Equilib, 2002, 200(1): 69–74. DOI: 10.1016/S0378-3812(02)00013-4 |
| [15] | Jouyban A, Acree W E. Comments concerning "solubility of anthracene in two binary solvents containing toluene"[J]. Fluid Phase Equilibria, 2003, 209(1): 155–159. DOI: 10.1016/S0378-3812(03)00078-5 |
| [16] | Prausnitz J M, Lichtenthaler R N, DeAzevedo E G. Molecular thermodynamics of fluid-phase equilibria[M]. England: Pearson Education, 1998. |
| [17] | Jia D, Li Y, Li Y, et al. Measurement and correlation of solubility of 2-chloro-4-ethylamino-6-isopropylamino-1, 3, 5-triazine in different organic solvents[J]. J Chem Eng Data, 2013, 58: 3 183–3 189. DOI: 10.1021/je400639m |
| [18] | Ahn J H, Kim J K, Kim H S, et al. Solubility of 1, 1-diamino-2, 2-dinitroethylene in N, N-dimethylform amide, dimethyl sulfoxide, and N-methyl-2-pyrrolidone[J]. J Chem Eng Data, 2009, 54: 3 259–3 260. DOI: 10.1021/je900235s |
 2017, Vol. 34
2017, Vol. 34





