2. 化学工程联合国家重点实验室, 天津 300072
2. State Key Laboratory of Chemical Engineering, Tianjin 300072, China
气液分离器广泛应用于石油、化工以及天然气加工等行业,它将气体中的雾沫分离开,从而减少因雾沫夹带导致的返混以提高效率,改善操作,同时净化尾气,减少大气污染等。
在各种类型的商业化气液分离器中,丝网除沫器是使用范围最广泛的[1]。因为丝网除沫器结构简单体积小,除沫效率高,阻力小,质量轻,安装、操作、维修方便,用于气液分离装置中可有效控制气体夹带的液滴量,保证传质效率,降低有价值物料的损失。尽管丝网除沫器已经广泛应用于各种工业生产中,但是关于丝网除沫器的工业设计目前依然依赖于Souders和Brown在20世纪30年代提出的基本原理[2],能够参考的数据和文献十分有限[3-7], 且绝大部分是研究多层式结构[8-9],对于缠绕式结构的研究几乎没有报道。因此十分有必要对缠绕式丝网除沫器进行深入研究。
本研究采用多种不同结构的缠绕式丝网除沫器,利用空气-水物系进行基础性实验研究,考察气速、丝网除沫器的比表面积、丝径以及除沫器床层厚度对分离效率的影响,同时建立相应的数学模型,并将数学模型的计算结果与实验结果进行比较,以期为缠绕式丝网除沫器的工业设计提供可靠的依据。
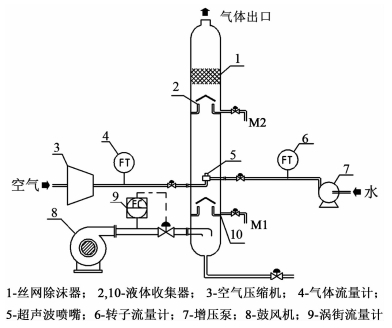
1 实验部分实验装置及流程如图 1所示。实验装置主体外壳由有机玻璃制造,内径为200 mm。
|
| 图 1 实验装置流程图 Figure 1 Schematic diagram of experiment apparatus |
| |
实验在标准环境条件 (T=25 ℃,P=101.13 kPa) 下进行。水经过增压泵7达到60 kPa压力,经转子流量计6调节流量为45 L·h-1,进入超声波喷嘴5;空气压缩机3提供350 kPa压缩空气,经气体流量计4调节流量为240 L·min-1,同样进入超声波喷嘴5。在喷嘴喉管处液体被高速压缩空气分散为细小雾滴,液滴被鼓风机8提供的气流夹带向上运动。鼓风机产生的气体流量由涡街流量计9控制。
气流中夹带的大液滴因重力作用,脱离气流,滴落至液体收集器10;非垂直运动的液滴与管壁碰撞,沉积于管壁上,向下流动,汇聚于液体收集器10;小液滴随着气流穿过丝网除沫器1,其中一部分液滴被丝网除沫器分离滴落至液体收集器2,另一部分液滴则随着气流由气体出口逃逸。液体收集器2、10收集的液体待分离过程达到稳定时,经阀门排出并待排出流量恒定时收集液体,取样时间为5 min,用电子天平对样品进行称重得到质量分别为M2和M1。液体收集器2收集的液体包括除沫器分离的液滴以及液体收集器挡板分离的液滴,故进行空塔 (不含丝网除沫器) 实验,得到相同气速下液体收集器挡板分离的液体质量m。实验利用称量法将喷嘴进口的液体体积流量换算为质量流量,为了避免实验误差,测量5 min内的平均质量流量,分别测量5组平行样,这5次测量的平均质量流量差不超过2%时,其平均值即可作为本次实验的液体进口质量流量m0。因此可以得到取样时间内液体的总进料量M0。分离效率η按式 (1) 计算。
| $ \eta = \frac{{被捕集的液体量}}{{进入丝网除沫器的液体量}} = \frac{{{M_2} - m}}{{{M_0} - {M_1}}} $ | (1) |
实验中所采用的丝网除沫器的直径为200 mm,制作材料为316 L不锈钢,丝网除沫器的规格如表 1所示。
| 编号 | A | B | C | D | E | F | G | H | I | J |
| 比表面积/(m2·m-3) | 212 | 212 | 212 | 205.5 | 375 | 579 | 860 | 212 | 212 | 212 |
| 空隙率/% | 98.79 | 98.79 | 98.79 | 98.61 | 97.47 | 96.09 | 94.20 | 99.36 | 99.10 | 98.48 |
| 丝径/mm | 0.228 | 0.228 | 0.228 | 0.27 | 0.27 | 0.27 | 0.27 | 0.12 | 0.17 | 0.286 |
| 厚度/mm | 65 | 100 | 150 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
当气液两相流通过丝网除沫器时,丝网阻碍气流前进,使气流多次改变运动速度和运动方向,这些改变引起液滴对丝网产生惯性碰撞、重力沉降、直接拦截、布朗扩散、静电吸引等作用[10]而使液滴聚集。由于液滴粒径一般大于1 μm,质量极小,且大部分呈电中性,故Holmes等[11]认为丝网除沫器主要的分离机理为:惯性碰撞和直接拦截。
惯性碰撞是丝网除沫器最主要的分离机理。当液滴随气流以一定的速度垂直向金属丝方向运动时,气液两相流受阻即需要改变运动方向以绕过金属丝。密度较大的液滴由于惯性较大,不能同气流一起及时改变运动方向,而是继续保持直线运动,直到与丝网发生碰撞而被捕集,形成大液滴后自丝网滴落分离,这种分离方式称为惯性碰撞分离。对于单根金属丝的惯性碰撞分离效率通常与St有关[12-13],即:
| $ St = \frac{{{\rho _{\rm{l}}}ud_{\rm{d}}^2}}{{18{\mu _{\rm{g}}}{d_{\rm{w}}}}} $ | (2) |
式 (2) 中ρl为液相密度 (kg·m-3),u为气体表观速度 (m·s-1),dd为液滴粒径 (m),μg为气体运动黏度 (m2·s-1),dw为金属丝丝径 (m)。
直接拦截是气流中的液滴粒径较小或者气速较低时,液滴的惯性较小,在突然改变方向时,液滴不能够脱离气流,而是随着气流一起绕过金属丝。但如果液滴与金属丝的距离足够小时 (液滴圆心与金属丝的距离小于液滴的半径),液滴便能与金属丝接触从而被捕集。Chen[14]提出直接拦截的分离效率和液滴粒径与金属丝丝径之比有关:
| $ {\eta _{\rm{r}}} = \left( {1 + R} \right) - \frac{1}{{1 + R}} $ | (3) |
式 (3) 中R为液滴粒径与金属丝丝径之比,
图 2~4表示丝网除沫器分离效率随气速的变化。如图所示,丝网除沫器的分离效率随气速的增大,呈现先增大后减小的变化。这是因为:1) 在较低气速下,只有小液滴能够克服重力作用到达丝网除沫器,由于小液滴的惯性和粒径较小,根据分离机理可知其惯性分离效率及直接拦截分离效率都较小,因此在较低气速下分离效率较低;2) 增加气速可以增大液滴的运动速度及粒径[15],从而增大惯性碰撞分离效率和直接拦截分离效率,因此分离效率随着气速的增大而增大;3) 当气速增大到临界值即分离效率达到最大值时,分离效率随着气速的增加迅速降低,这是由于在高气速下,被丝网捕集而聚集的大液滴不能够在重力的作用下滴落分离,而是附着在丝网壁上,这就造成除沫器内液体大量积聚。当气速继续增大时,这些液滴就会重新被高速气流夹带出除沫器,从而造成分离效率迅速下降[10, 14],这种现象称为二次夹带。

|
| 图 2 不同气速下比表面积对分离效率的影响 Figure 2 Effect of surface area on the separation efficiency at different gas velocities |
| |

|
| 图 3 不同气速下丝径对分离效率的影响 Figure 3 Effect of wire diameter on the separation efficiency at different gas velocities |
| |
|
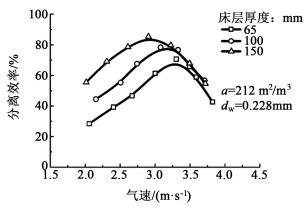
| 图 4 不同气速下床层厚度对分离效率的影响 Figure 4 Effect of packing thickness on the separation efficiency at different gas velocities |
| |
Brunazzi和Paglianti[16]实验测量了丝径为0.27 mm,比表面积为267 m2·m-3,床层厚度为150 mm的丝网除沫器分离粒径为3.5 μm的液滴的分离效率:当气速为2 m·s-1时,分离效率为45%。当气速降为1 m·s-1时,分离效率只有约14%。El-Dessouky[17]实验测量了丝径为0.28 mm,比表面积为148 m2·m-3,床层厚度为200 mm的丝网除沫器在气速为1.26 m·s-1下分离粒径为1~3 μm的液滴的分离效率,结果分别为38%、44%和49%。对比本研究实验数据,表明本实验在低气速下的分离效率的测量结果是准确的。
3.2 比表面积的影响图 2表示床层厚度为100 mm,丝径为0.27 mm的丝网除沫器的比表面积对分离效率的影响。
由图 2可见,在未发生二次夹带的情况下,分离效率随着比表面积的增加而增加。这是由于对于丝径一定的丝网除沫器,比表面积增加导致其空隙率减小,即气流通过的自由截面积减少,这将使气流中液滴与丝网发生碰撞被捕集的概率增加,从而促进了液滴的分离,提高了分离效率[17]。此外,由图 2中可知,比表面积越大,发生二次夹带的气速越小,这是因为:比表面积越大,空隙率越小,丝网捕集的液滴就越多,即丝网除沫器内的持液量越大,从而易发生二次夹带。
3.3 丝径的影响图 3表示丝径对分离效率的影响。测试的丝网除沫器的床层厚度均为100 mm,比表面积为212 m2·m-3。
由图 3可见,在未发生二次夹带前,丝径越小,分离效率越大。这是因为:气速一定时,丝径越小,液滴粒径与金属丝丝径之比就越大,由式 (3) 可知直接拦截分离效率也就越大。另外,从图 3中可以得出,气速越低,丝径对分离效率的影响越明显,这是因为气速越小,液滴粒径也就越小,丝径越小就越能捕获小尺寸的液滴[18],因此丝径对分离效率的影响越明显。但是当气速较大时,丝径对分离效率的影响较小,这是因为:当比表面积一定时,丝径越小,空隙率越大,这将降低气流中液滴与丝网发生碰撞被捕集的概率,不利于提高分离效率,而且气速越大,空隙率的影响越明显[15],这就导致了在较大气速下,丝径对分离效率的影响很小。
3.4 床层厚度的影响图 4表示丝网除沫器床层厚度对分离效率的影响。
由图 4可见,在未发生二次夹带前,分离效率随着丝网除沫器的床层厚度的增加而增加。这是因为床层厚度越大,气流通过除沫器需要的时间就越长,气流中的液滴与丝网发生碰撞的概率也就越大,从而提高了分离效率。
4 数学模型根据实验结果发现,在未发生二次夹带前,分离效率随着气速、丝网除沫器的比表面积、丝径以及床层厚度的变化具有一定的规律。因此本研究根据实验结果、缠绕式丝网除沫器的分离机理以及空间结构建立了数学模型,拟合了预测发生二次夹带之前的分离效率的数学模型,最后对比了模型计算值与实验结果。
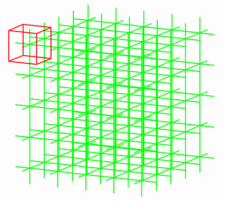
4.1 模型建立虽然利用实际的几何结构参数建立复杂的数学模型可以对事物进行更全面的描述,但是复杂的模型必定需要更加复杂的数值计算,而更加复杂的计算却不能相应地增加模型预测的准确性[16]。因此本研究根据缠绕式丝网除沫器的结构特征,提出一个简化模型 (图 5):将厚度为H的丝网除沫器分割为n层正方体网格单元,每个网格单元边长为L,并假设:a) 未发生二次夹带;b) 网格单元内中没有液体的积聚;c) 气体经过每层网格后都进行均匀的再分布;d) 每个网格单元分离效率相同。
|
| 图 5 网格模型 Figure 5 Grid model |
| |
每个网格单元包含三根相互垂直且长度均为L的金属丝,网格单元的特征长度L定义可由空隙率ε表示
| $ \varepsilon = 1 - \frac{{3\pi d_{\rm{w}}^2}}{{4{L^2}}} $ | (4) |
故网格的特征长度L的表达式为:
| $ L = \sqrt {\frac{{3\pi d_{\rm{w}}^2}}{{4\left( {1 - \varepsilon } \right)}}} $ | (5) |
网格单元层数n的定义式为:
| $ n = {\rm{int}}\left[ {\frac{H}{L}} \right] $ | (6) |
若将式 (1) 定义的分离效率用液滴浓度表示,则有:
| $ \eta = \frac{{{C_0} - {C_n}}}{{{C_0}}} $ | (7) |
其中C0为进入第一层网格气体中的液滴浓度,为了计算分离效率,我们必须知道分离后气体中的液滴浓度Cn。若知道C0,根据之前的假设我们可以得到气体经过每层网格分离后的液滴浓度。
经过第1层网格单元分离后的液滴浓度C1可以分为3个部分,即
| $ {C_1} = {C_{{\rm{1i}}}} + {C_{{\rm{1r}}}} + {C_{{\rm{1c}}}} $ | (8) |
1) 气体经过惯性碰撞后的剩余液滴浓度为C1i:
| $ {C_{{\rm{1i}}}} = {C_0}\frac{{{d_{\rm{w}}}L + {d_{\rm{w}}}(L - {d_{\rm{w}}})}}{{{L^2}}}(1 - {\eta _{\rm{i}}}) $ | (9) |
式 (9) 中dwL+dw(L-dw) 表示每个网格内液滴与丝网发生惯性碰撞的横截面积Si,ηi为惯性碰撞分离效率。
2) 气体经过直接拦截后的剩余液滴浓度C1r:
| $ \begin{array}{c} {C_{{\rm{1r}}}} = \\ {C_0}\frac{{\frac{1}{4}\pi (d_{{\rm{av}}}^2 + 2{d_{{\rm{av}}}}{d_{\rm{w}}}) + {d_{{\rm{av}}}}(4L - 3{d_{{\rm{av}}}} - 4{d_{\rm{w}}})}}{{{L^2}}}(1 - {\eta _{\rm{r}}}) \end{array} $ | (10) |
式 (10) 中
3) 未经过任何分离作用的剩余液滴浓度C1c:
| $ {C_{1{\rm{c}}}} = {C_0}\frac{{{L^2} - {S_{\rm{i}}} - {S_{{\rm{r1}}}} - {S_{{\rm{r2}}}}}}{{{L^2}}} $ | (11) |
将式 (9)、(10) 和 (11) 代入上式进一步化简可得:
| $ {C_1} = {C_0}(1 - \frac{{{S_{\rm{i}}}}}{{{L^2}}}{\eta _{\rm{i}}} - \frac{{{S_{{\rm{r1}}}} + {S_{{\rm{r2}}}}}}{{{L^2}}}{\eta _{\rm{r}}}) $ | (12) |
同样,通过第2层网格单元后的液滴浓度C2分为3个部分:
1) 气体经过惯性碰撞后的剩余液滴浓度C2i
| $ {C_{{\rm{2i}}}} = {C_1}\frac{{{S_{\rm{i}}}}}{{{L^2}}}(1 - {\eta _{\rm{i}}}) $ | (13) |
2) 气体经过直接拦截后的剩余液滴浓度C2r:
| $ {C_{{\rm{2i}}}} = {C_1}\frac{{{S_{{\rm{r1}}}} + {S_{{\rm{r2}}}}}}{{{L^2}}}(1 - {\eta _{\rm{r}}}) $ | (14) |
3) 未经过任何分离作用的剩余液滴浓度C2c:
| $ {C_{{\rm{2c}}}} = {C_1}\frac{{{L^2} - {S_{\rm{i}}} - {S_{{\rm{r1}}}} - {S_{{\rm{r2}}}}}}{{{L^2}}} $ | (15) |
因此C2的表达式为:
| $ {C_2} = {C_1}(1 - \frac{{{S_{\rm{i}}}}}{{{L^2}}}{\eta _{\rm{i}}} - \frac{{{S_{{\rm{r1}}}} + {S_{{\rm{r2}}}}}}{{{L^2}}}{\eta _{\rm{r}}}) $ | (16) |
将式 (12) 代入式 (16) 可得:
| $ {C_2} = {C_0}{\left( {1 - \frac{{{S_{\rm{i}}}}}{{{L^2}}}{\eta _{\rm{i}}} - \frac{{{S_{{\rm{r1}}}} + {S_{{\rm{r2}}}}}}{{{L^2}}}{\eta _{\rm{r}}}} \right)^2} $ | (17) |
以此类推可得通过第n层网格单元后的液滴浓度Cn:
| $ {C_n} = {C_0}{\left( {1 - \frac{{{S_{\rm{i}}}}}{{{L^2}}}{\eta _{\rm{i}}} - \frac{{{S_{{\rm{r1}}}} + {S_{{\rm{r2}}}}}}{{{L^2}}}{\eta _{\rm{r}}}} \right)^n} $ | (18) |
将C0和Cn的表达式代入式 (7) 就可得到分离效率η的模型表达式为:
| $ \eta = 1 - {\left( {1 - \frac{{{S_{\rm{i}}}}}{{{L^2}}}{\eta _{\rm{i}}} - \frac{{{S_{{\rm{r1}}}} + {S_{{\rm{r2}}}}}}{{{L^2}}}{\eta _{\rm{r}}}} \right)^n} $ | (19) |
模型表达式 (19) 中有3个未知参数:平均液滴粒径dav、惯性碰撞分离效率ηi以及直接拦截分离效率ηr。
Guseinov等[19]提出丝网除沫器前的管路中的平均液滴粒径可以通过下列关联式进行估算:
| $ {d_{{\rm{av}}}} = {(\frac{{{R_{{\rm{cr}}}}}}{{0.12}}{(\frac{{{\rho _{{\rm{l}}{{\rm{u}}^2}}}}}{{{\sigma _{\rm{l}}}}})^{\frac{3}{7}}}{(\frac{{{\rho _{\rm{G}}}}}{{{\rho _{\rm{l}}}}})^{\frac{{ - 1}}{7}}})^{\frac{7}{4}}} $ | (20) |
其中σl为液体的表面张力,ρG为气体密度,Rcr为临界液滴半径:
| $ {R_{{\rm{cr}}}} = 0.75{\left( {\frac{{{\mu _{\rm{g}}}{d_{\rm{w}}}}}{{2u{\rho _{\rm{l}}}}}} \right)^{1/2}} $ | (21) |
因此本研究采用上述关联式计算平均液滴粒径dav。
目前计算直接拦截分离效率ηr的经验式中,使用较普遍的是Chen[14]提出的经验式,即式 (3)。因此采用式 (3) 来对ηr进行计算。
在文献中可以找到许多经验式来计算惯性碰撞分离效率ηi,其中使用最普遍是Langmuir和Blodgett[20]提出的经验式,但是Lucas[21]指出Langmuir和Blodgett提出的经验式不适用于丝网间距较小的除沫器的分离效率计算。文献[11, 16]研究表明惯性碰撞分离效率ηi与St数有关,同时根据各参数对分离效率的影响的实验结果。本研究提出如下关联式:
| $ {\eta _{\rm{i}}} = a{R^b}{\left( {1 - \varepsilon } \right)^c}S{t^d} $ | (22) |
其中模型参数a, b, c和d通过实验进行关联。经关联后的参数值分别为:a=0.0051,b=0.8639,c=-0.8639,d=0.8811。
若将式 (3)、(20)、(21) 以及 (22) 代入式 (19) 就可得知影响丝网除沫器分离效率的所有因素,即:
| $ \eta = f({\rho _{\rm{G}}},{\rm{ }}{\rho _{\rm{l}}},{\rm{ }}{\sigma _{\rm{l}}},{\mu _{\rm{g}}},u,{\rm{ }}{d_{\rm{w}}},\varepsilon ,H) $ | (23) |
通过式 (23) 可知压力和温度一定时,分离效率只和气速、丝网除沫器丝径、空隙率 (或者比表面积) 以及床层厚度有关。将各实验参数代入式 (19),可以得到丝网除沫器在不同气速下的分离效率。
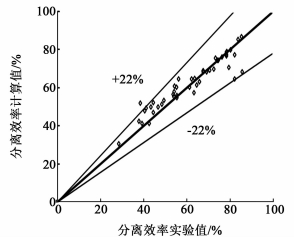
图 6为未发生二次夹带时模型计算结果与实验时数据的比较。
|
| 图 6 模型值与实验值的对比 Figure 6 Comparison between the model and experimental measured values |
| |
图 6说明在未发生二次夹带时,分离效率的模型关联式的计算值与实验结果基本吻合,平均误差为6.49%,误差在±22%以内,说明该模型可以对缠绕式丝网除沫器未发生二次夹带时的分离效率进行预测。
5 结论与展望1) 当未发生二次夹带时,增大比表面积、床层厚度以及气体速度或者减小丝径,均有利于提高分离效率。当发生二次夹带时,分离效率随着气速的增加而迅速减小。
2) 根据实验结果以及缠绕式丝网除沫器的空间结构建立了数学模型,并拟合了预测未发生二次夹带时的分离效率的数学模型关联式。通过比较模型关联式的计算结果和实验结果,发现该模型关联式具有较好的准确性,能够对缠绕式丝网除沫器的工业设计提供一定的参考。
3) 通过实验数据拟合获得的模型参数表明,气液相密度、空气黏度、液体表面张力、液滴粒径、除沫器比表面积、丝径、床层厚度以及气速是影响缠绕式丝网除沫器分离效率的主要因素。
4) 对于发生二次夹带后,分离效率的变化规律以及模型预测是今后工作的重点。
| [1] | Fabian P, Hennessey P, Neuman M, et al. Demystifying the selection of mist eliminators; Part 2:The applications[J]. Chemical Engineering, 1993, 100(12) : 106–111. |
| [2] | Souders M, Brown G G. Design of fractionating columns Ⅰ. Entrainment and capacity[J]. Industrial & Engineering Chemistry, 1934, 26(1) : 98–103. |
| [3] | York O H. Performance of wire-mesh demisters[J]. Chemical Engineering Progress, 1954, 50(8) : 421–424. |
| [4] | York O H, Poppele E W. Wire mesh mist eliminators[J]. Chemical Engineering Progress, 1963, 59(6) : 45–50. |
| [5] | York O H, Poppele E W. Two stage mist eliminators for sulfuric acid plants[J]. Chem Eng Prog, 1970, 66(11) : 67–72. |
| [6] | Bell C G, Strauss W. Effectiveness of vertical mist eliminators in a cross flow scrubber[J]. Journal of the Air Pollution Control Association, 1973, 23(11) : 967–969. DOI: 10.1080/00022470.1973.10469867 |
| [7] | Calvert S, Jashnani I L, Yung S. Entrainment separators for scrubbers[J]. Journal of the Air Pollution Control Association, 1974, 24(10) : 971–975. DOI: 10.1080/00022470.1974.10470001 |
| [8] | 孙正伟. 除沫器流动阻力与分离特性研究[D]. 辽宁大连: 大连理工大学, 2012 Sun Zhengwei. Experimental investigation on flow resistance and separating performance of demister[D]. Liaoning Dalian:Dalian University of Technology, 2012(in Chinese) |
| [9] | 甄妮. 液滴在蒸汽携带下撞击丝网除沫器的模拟研究[D]. 辽宁大连: 大连理工大学, 2014 Zhen Ni. Numerical simulation of droplet entrained by vapor across the wire mesh demister[D]. Liaoning Dalian:Dalian University of Technology, 2012(in Chinese) |
| [10] |
虢国成, 王满生. 丝网气液分离器分离机理分析研究[J].
食品与机械, 2010(4) : 98–101.
Guo Guocheng, Wang Mansheng. Separation mechanism analysis of wire-mesh gas-liquid separator[J]. Food & Machinery, 2010(4) : 98–101. |
| [11] | Holmes T L, Chen G. Design and selection of spray/mist elimination equipment[J]. Chem Eng, 1984, 91(21) : 82–89. |
| [12] | Brunazzi E, Paglianti A. Conventional and complex knitted mesh mist eliminators[J]. Chemical Engineering & Technology, 2001, 24(11) : 1199–1204. |
| [13] | Setekleiv A E, Svendsen H F. Operation and dynamic behavior of wire mesh pads[J]. Chemical Engineering Science, 2012, 68(1) : 624–639. DOI: 10.1016/j.ces.2011.10.027 |
| [14] | Chen C Y. Filtration of aerosols by fibrous media[J]. Chem Rew, 1995, 55(3) : 595–623. |
| [15] | Al-Dughaither A S, Ibrahim A A, Al-Masry W A. Investigating droplet separation efficiency in wire-mesh mist eliminators in bubble column[J]. Journal of Saudi Chemical Society, 2010, 14(4) : 331–339. DOI: 10.1016/j.jscs.2010.04.001 |
| [16] | Brunazzi E, Paglianti A. Design of wire mesh mist eliminators[J]. AIChE J, 1998, 44(3) : 505–512. DOI: 10.1002/(ISSN)1547-5905 |
| [17] | El-Dessouky H T, Alatiqi I M, Ettouney H M, et al. Performance of wire mesh mist eliminator[J]. Chemical Engineering and Processing:Process Intensification, 2000, 39(2) : 129–139. DOI: 10.1016/S0255-2701(99)00033-1 |
| [18] |
沈胜强, 甄妮, 牟兴森. 丝网除沫器除沫效率的数值模拟[J].
核动力工程, 2014, 35(5) : 172–177.
Shen Shengqiang, Zhen Ni, Mou Xingsen. Determiantion of separation efficiency in wire mesh mist eliminator by CFD[J]. Nuclear Power Engineering, 2014, 35(5) : 172–177. |
| [19] | Guseinov C S, Asaturjan A S. Determination of drop modal size in two-phase flow[J]. Appl Chemistry, 1977, 50(4) : 848–853. |
| [20] | Langmuir I, Blodgett K B. A Mathematical investigation of water droplet trajectories[M]. Army Air Forces Headquarters: Air Technical Service Command, 1946 . |
| [21] | Lucas R L. Gas-Solid separations[M]. New York: McGraw-Hill, 1983 . |
 2017, Vol. 34
2017, Vol. 34





