直接接触式换热器具有腐蚀小、不结垢、换热效率高、传热温差小、压降小和投资费用低等优点,因此具有广泛的应用前景[1-3]。由于直接接触式换热过程的复杂性,目前对于直接接触换热器的设计远不如间壁式换热器那样完善。鼓泡塔式直接接触换热器是最简单、常用的结构型式,主要用于蒸发过程,对其研究也比较多[4-8]。Siqueiros等[9]研究了1.9 m鼓泡塔中戊烷-水直接接触式蒸发换热过程,在分散相与连续相流速比为0.035~0.110时,体积换热系数仅为0~9 kW/(m3·K)。Celata等[10]进行了R114在水中直接接触式蒸发实验,发现温差在10 K下体积换热系数变化范围为0~100 kW/(m3·K)。另外,Boehm[11]发现鼓泡塔内存在液滴尾流,并随着汽化的进行易出现返混等阻碍换热的因素,板式塔和填料塔也可作为直接接触换热器,并认为可以改善鼓泡塔的不足。但是目前填料塔的研究主要集中在冷凝方面或者烟气与液体换热方面。Li等[12]研究了直接接触式冷凝器中水蒸气-空气/汽体冷凝过程温度、湿度和冷凝率的变化,并建立了一维模型进行比较。Alnaimat等[13]建立了瞬态一维守恒方程来分析直接接触式蒸发器和冷凝器中的水-空气/汽体的传热和传质过程,并预测了温度和湿度等参数的变化。本研究重点从宏观方面系统地考察填料的强化性能,并研究塔中不同参数对体积换热系数与汽化高度的影响。
本研究以正戊烷-水为物系,采取并流操作,研究填料强化后鼓泡塔直接接触式蒸发换热性能,并考察了分散相流量、温差和分布器孔径对汽化高度和体积换热系数的影响。
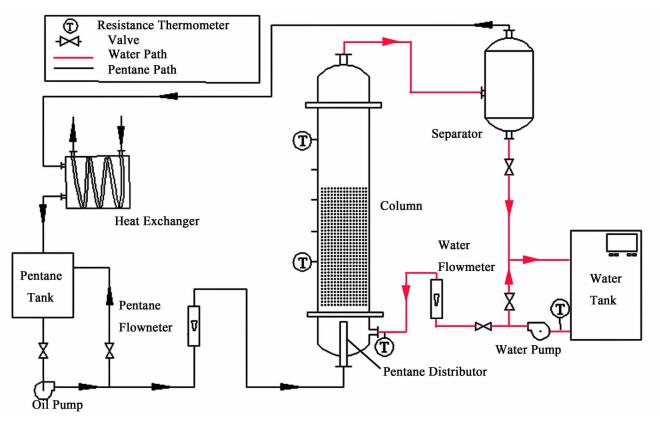
1 实验与理论分析 1.1 实验装置与流程实验选择正戊烷和自来水为工作介质,正戊烷为分散相,水为连续相,实验装置示意图见图 1。鼓泡塔尺寸为Φ80 mm×1 400 mm,由普通玻璃制成,共有塔身和封头两部分,塔身与封头通过法兰连接。其中塔身高为1 000 mm,封头为200 mm,塔身一侧安装有5个间隔为200 mm的测温孔,用于热电阻测量塔内流体温度。塔底部连接材质为PVC的棒状分布器(Φ20 mm×100 mm),用于分散戊烷液体。
|
| 图 1 实验装置示意图 Figure 1 Schematic diagram of experimental setup |
| |
实验采取顺流操作,正戊烷液体和水从塔底进入鼓泡塔内,经过相间换热,气液混合物从塔顶进入到气液分离器,分离出戊烷蒸汽和水,戊烷蒸汽进入列管式冷凝器中冷凝成戊烷液体后流回到戊烷储罐,回收的液态戊烷再经过油泵送入塔中进行换热;另一方面,从气液分离器中分离出的水直接流回到恒温储水罐中,再由水泵输送入塔中。
在储水罐中加入1个2 kW加热棒来实现水的加热,采用水泵强化水循环以维持罐内水温均匀,通过控温装置来实现水温恒定。戊烷通过油泵进入转子流量计,油泵为隔膜泵,采用旁路调节。填料采用10 mm×10 mm的不锈钢θ环散装填料,填充高度为600 mm。
分散相和连续相的流量采用2个不同型号的转子流量计来测量,戊烷流量测量采用量程为0~25 L/h的LZB-4型流量计,戊烷流量为13.260、17.238、19.890和23.868 L/h,水流量测量采用量程为4~400 L/h的LZB-10型流量计,精度都为1.0 L/h,水流量恒定为160 L/h。测温点总共7个,采用Pt100热电阻来测量塔内流体的实际温度,精度为0.1 ℃,尺寸为Φ2 mm×100 mm,热电阻通过数据采集系统导入电脑,用于计算体积换热系数。实验中,采用红外热像仪(型号为SAT-G90,最小测量温度为0.1 ℃)来测量塔内流体的连续温度轴向分布趋势,从而得到汽化高度。
实验参数的误差分析总结如表 1所示。
| 参数 | 误差 |
| 流量(Gd) | ±1% |
| 温度(T) | ±0.1℃ |
| 分布器孔径(d) | ±3% |
| 温差(△T) | ±2.6% |
| 汽化高度(H) | ±2.1% |
| 体积换热系数(Uv) | ±3.7% |
汽化高度是反映直接接触式蒸发换热性能的重要参数之一。通常将汽化高度定义为戊烷完全汽化所需的高度,可以通过温度轴向分布趋势来判断汽化高度。
实验中,相对于水的流量来说,戊烷的流量较小,热电阻测量的流体温度可近似认为是连续相水的温度,而蒸发过程中戊烷的温度近似认为是标准状态下沸点温度(36.1 ℃)。蒸发过程中,水与戊烷不断换热,水放出热量,水温沿塔轴向上逐渐降低,蒸发完全后,水温基本维持不变,根据轴向水温变化趋势可以判断汽化是否进行完全,随即也可获得汽化高度。热电阻测出塔内水的实际温度,但是热电阻间距较宽,当汽化高度处于2个热电阻之间时,则无法准确测出,因此采用红外热像仪来测量塔内轴向连续温度分布。红外热像仪拍摄得到红外图像,红外图像经SatIrReport软件处理得到相应的汽化高度。
1.2.2 体积换热系数整个蒸发过程中热量分为塔内塔内流体蒸发潜热、流体与环境显热、流体间显热。相对于潜热来说,显热很小,可以忽略,因而实验换热率为:
| $ Q = {m_{\rm{c}}}{c_{{\rm{pc}}}}\left( {{T_1}-{T_2}} \right) $ | (1) |
其中mc为水质量流量,cpc为水的比热容,T1、T2分别为水的进口温度和出口温度。由于换热面积很难准确测定,所以采用体积换热系数,按式(2)计算:
| $ {U_{\rm{v}}} = Q/AH\Delta T $ | (2) |
其中Q为换热率,A为塔截面积,H为汽化高度,△T为温差。为了减小误差,实验中温差采用对数平均温差,表达式为:
| $ \Delta T = \frac{{\left( {{T_1}- {T_2}} \right)}}{{\lg \left[{\left( {{T_1}-{T_{\rm{d}}}} \right)/\left( {{T_1}-{T_{\rm{d}}}} \right)} \right]}} $ | (3) |
其中Td为戊烷沸点。
2 结果与讨论 2.1 填料的强化作用 2.1.1 流体流型实验中流体流型主要受戊烷流量和连续相进口温度影响较大。鼓泡塔中,未加入填料时,随着戊烷流量与连续相进口温度的增加,塔中流体径向运动增加,湍动加强,剧烈时,在塔顶部出现流体轴向返混,从而使塔中流型较复杂,如图 2b)所示。加入填料后,填料极大阻碍了流体的径向运动和轴向运动,另外由于填料的切割作用,戊烷液滴的尺寸受到限制,使得流型平缓,如图 2a)所示。

|
| 图 2 流体流型图(塔高为300~500 mm) Figure 2 Liquid flow pattern (column height of 300~500 mm) |
| |
图 3为戊烷流量为23.868 L/h,分布器孔径为2.5 mm时加有填料和未加填料的鼓泡塔中体积换热系数与温差关系的对比图。

|
| 图 3 加填料与未加填料的体积换热系数与温差关系对比图 Figure 3 Volumetric heat transfer coefficient against temperature difference with packing and without packing |
| |
通过观察发现:加填料前后,鼓泡塔中的体积换热系数与温差的关系没有变化,但是加有填料的体积换热系数约为未加填料的体积换热系数的2倍,这也说明填料对鼓泡塔中换热性能具有一定的强化作用。塔中加入填料后,一方面,由于填料切割与阻碍,对戊烷液滴尺寸有一定的限定作用,同时也能增加戊烷在塔内的停留时间,促进戊烷的蒸发;另一方面,填料在一定程度上能减小流体的轴向运动与径向运动,在一定程度上能减小返混,这些都能加强塔内的换热性能。
2.2 加填料的鼓泡塔中的汽化高度 2.2.1 分散相流量对汽化高度的影响图 4显示了分散相流量(Gd)对汽化高度(H)的影响。

|
| 图 4 汽化高度与分散相流量关系图 Figure 4 Evaporative height against pentane flow rate |
| |
由图 4中所示,分布器孔径(d)为2.5 mm且连续相进口温度不变时,汽化高度随着分散相流量的增加而增加。这是因为分散相流量增加,分布器孔径不变,单位时间进入塔内的戊烷液滴增加,需汽化的戊烷总量增加,在连续相热容量不变时,戊烷液滴完全汽化所需的高度增加,因而汽化高度增加。
2.2.2 温差对汽化高度的影响图 5显示汽化高度与对数平均温差关系。

|
| 图 5 汽化高度与对数平均温差关系图 Figure 5 Evaporative height against log-mean temperature difference |
| |
由图 5可看出,在戊烷流量不变时,汽化高度随对数平均温差(△T)的增加而减小。当温差为0~4 ℃时,汽化高度随温差的增加而迅速降低,当温差△T>8 ℃时,汽化高度变化比较平稳。首先,一定的戊烷液滴进入塔内进行蒸发换热,其它条件不变时,温差增大时,换热推动力增加,汽化加快,汽化所需的高度降低。其次,当温差较小时,换热推动力很小,戊烷汽化速率较小,温差增大对戊烷汽化速率增加作用较强;最后,当温差增大到一定的数值时,温度推动力足够大,戊烷与水换热迅速汽化,而戊烷汽化所需的高度同时受连续相热容量影响,并不能无限制减小,使得此时温差增加对汽化高度影响很小。
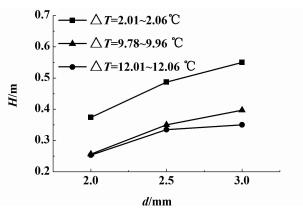
2.2.3 分布器孔径对汽化高度的影响Sideman等[14]研究了分布器孔径(0.5、1.5和2.5 mm)对戊烷-水直接接触式蒸发系统的影响,认为汽化高度随分布器孔径的增大而增大,体积换热系数随着分布器孔径的增大而减小。Seetharamu等[15]研究了不同分布器孔径(0.5、1.0、1.5和2.0 mm)时R113在水中直接接触式蒸发换热,发现体积换热系数随分布器孔径的增大而减小。依据文献[14]和[15],同时为了更好地获得不同分布器孔径时填料的强化性能,本实验取分布器孔径为2.0、2.5和3.0 mm。图 6为分布器孔径(d)对汽化高度的影响。
|
| 图 6 分布器孔径对汽化高度的影响 Figure 6 Evaporative height against distributor aperture |
| |
由图 6中可以看出,当戊烷流量和温差一定时,分布器孔径增大,汽化高度总体趋势增加,但分布器为2.5和3.0 mm时增加趋势并不明显。分散相流量一定时,分布器孔径增大,分散相液滴初始尺寸增大,换热液滴数目减小,液滴群的总表面积减小,平均换热面积减小,汽化所需高度增加;但当分布器孔径较大时,由于填料的再分散作用,分布器的强化作用受到限制,使得分布器孔径对汽化高度的影响较小。
2.3 加填料的鼓泡塔中的体积换热系数体积换热系数(Uv)是衡量直接接触式蒸发换热性能的重要参数。体积换热系数的影响因素众多,如流体物性、流量、温度和液滴出口尺寸与汽化形态、塔器结构尺寸等。下面主要从分散相流量、温差、分布器孔径3个方面来讨论体积换热系数的变化。
2.3.1 分散相流量对体积换热系数的影响Sideman等[4]研究戊烷在水中蒸发时发现一定范围内体积换热系数随分散相流量的增加而增加,而连续相的影响几乎可以忽略。图 7显示了分散相流量对体积换热系数的影响。

|
| 图 7 体积换热系数与流量关系图 Figure 7 Volumetric heat transfer coefficient against pentane flow rate |
| |
当连续相进口温度和分布器孔径不变时,体积传热系数随分散相流量的增加而增加,这是因为当分散相流量增加时,进入塔内进行蒸发换热的戊烷液滴数量增加,而水的热容量足够用于戊烷的汽化,戊烷完全汽化时,整塔体积换热系数增加。从图 7中还可看出,当连续相进口温度较低时,体积换热系数增加趋势更大。
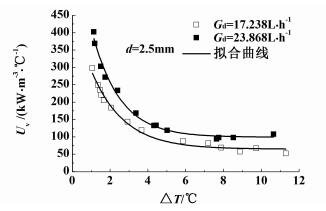
2.3.2 温差对体积换热系数的影响图 8为体积换热系数与对数平均温差的关系图。
|
| 图 8 体积换热系数与对数平均温差关系图 Figure 8 Volumetric heat transfer coefficient against log-mean temperature difference |
| |
图 8中显示:体积换热系数随对数平均温差的增加而减小,从实验拟合曲线看出,体积换热系数与温差近似成负幂指数关系。当对数平均温差△T为0~4 ℃时,体积换热系数随温差的增加而快速降低;当△T>8 ℃时,体积换热系数随温差的变化基本不变。分析原因如下:1)温差增大时,换热推动力增加,测量得出所需的汽化高度减小,根据公式(2)得出在换热率不变时,体积换热系数受温差与汽化高度乘积的影响,但根据公式(3)计算得到的温差比汽化高度对乘积影响更大,因而温差增大使得两者综合作用后仍增大,体积换热系数就减小。2)低温差(0~4 ℃)时,当温差提高时,汽化高度变化较大,且温差变化相对值较大,体积换热系数快速降低;而高温差(大于8 ℃)时,温差增加时,汽化高度变化不大,且温差变化相对值比低温差小,体积换热系数变化很小。因此,在低温段时可以通过提高温差来强化体积换热系数,但是在高温时必须考虑用其他方法来强化换热。
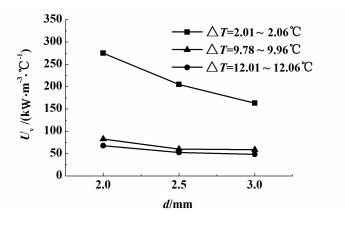
2.3.3 分布器孔径对体积换热系数的影响图 9表示体积换热系数受分布器孔径的影响。当分散相流量和温差不变时,分布器孔径减小,体积换热系数增加,这与Sideman等[14]研究的分布器孔径与体积换热系数的影响规律一致。低温差时体积换热系数增加比高温差时更明显。当分布器孔径增大,戊烷流量不变时,进入塔内的戊烷液滴平均直径增大,液滴群数目减小,使得液-液接触面积减小,换热速率减小,所需的汽化高度增加,戊烷完全汽化时,整塔体积换热系数减小。
|
| 图 9 分布器孔径对体积换热系数的影响 Figure 9 Volumetric heat transfer coefficient against distributor aperture |
| |
主要阐述了采用填料强化的鼓泡塔中正戊烷-水直接接触式蒸发换热实验,考察了分散相流量、温差、分布器孔径对汽化高度和体积传热系数的影响。实验得出以下结论:
1)当戊烷流量为23.868 L/h,分布器孔径为2.5 mm时,加填料的鼓泡塔中体积换热系数约为未加填料的2倍,填料在一定程度上能强化鼓泡塔的换热性能。
2)汽化高度随分散相流量的增加而升高;随对数平均温差的增加而减小,低温差(0~4 ℃)时,汽化高度随温差增加快速减小,高温差(△T>8 ℃)时,温差对汽化高度的影响很小;汽化高度随分布器孔径的增加而增加。
3)体积换热系数随分散量流量的增加而增加,随分布器孔径的增加而减小;体积换热系数与对数平均温差近似成负幂指数关系,低温差(0~4 ℃)时,体积换热系数随温差的增加快速减小,高温差(△T>8 ℃)时;体积换热系数基本不变。
| [1] |
章学来, 卢家才, 李瑞阳, 等. 直接接触式换热技术的研究进展[J].
能源技术, 2001, 22(1) : 1–5.
Zhang Xulai, Lu Jiacai, Li Ruiyang, et al. The research advancement of direct contact heat transfer technology[J]. Energy Technology, 2001, 22(1) : 1–5. |
| [2] |
章学来, 卢家才, 李瑞阳, 等. 直接接触式换热技术的研究进展(续)[J].
能源技术, 2001, 22(2) : 53–55.
Zhang Xuelai, Lu Jiacai, Li Ruiyang, et al. The research advancement of direct contact heat transfer technology[J]. Energy Technology, 2001, 22(2) : 53–55. |
| [3] |
靳登超, 王双平, 夏玉莲. 不互溶液体间直接接触传热的研究进展[J].
化学工业与工程, 2009, 26(6) : 543–546.
Jing Dengchao, Wang Shuangping, Xia Yulian. Progress in direct-contact heat transfer between immiscible liquids[J]. Chemical Industry and Engineering, 2009, 26(6) : 543–546. |
| [4] | Sideman S, Gat Y. Direct contact heat transfer with change of phase:Spray-Column studies of a three-phase heat exchanger[J]. AIChE Journal, 1966, 12(2) : 296–303. DOI: 10.1002/(ISSN)1547-5905 |
| [5] | Sideman S, Isenberg J. Direct contact heat transfer with change of phase:Bubble growth in three-phase systems[J]. Desalination, 1967, 2(2) : 207–214. DOI: 10.1016/S0011-9164(00)84138-7 |
| [6] | Song M, Steiff A, Weinspach P M. Nusselt number for direct contact evaporation of a moving ellipsoidal drop in an immiscible liquid[J]. Chemical Engineering Communications, 1996, 145(1) : 73–87. DOI: 10.1080/00986449608936469 |
| [7] | Song M, Steiff A, Weinspach P M. Parametric analysis of direct contact evaporation process in a bubble column[J]. International Journal of Heat and Mass Transfer, 1998, 41(12) : 1749–1758. DOI: 10.1016/S0017-9310(97)00241-X |
| [8] | Song M, Steiff A, Weinspach P M. Direct-Contact heat transfer with change of phase:A population balance mode[J]. Chemical Engineering Science, 1999, 54(17) : 3861–3871. DOI: 10.1016/S0009-2509(99)00029-9 |
| [9] | Siqueiros J, Bonilla O. An experimental study of a three-phase, direct-contact heat exchanger[J]. Applied Thermal Engineering, 1999, 19(5) : 477–493. DOI: 10.1016/S1359-4311(98)00068-4 |
| [10] | Celata G P, Cumo M, D'Annibale F, et al. Direct contact evaporation of nearly saturated R114 in water[J]. International Journal of Multiphase Flow, 1996, 38(8) : 1495–1504. |
| [11] | Robert F B. Direct-Contact heat transfer[C]//Adrian Bejan and Allan D. Kraus. Heat transfer handbook. NewYork:Wiley-Interscience, 2003 |
| [12] | Li Y, Klausner J F, Mei R, et al. Direct contact condensation in packed beds[J]. International Journal of Heat & Mass Transfer, 2006, 49(25) : 4751–4761. |
| [13] | Alnaimat F, Klausner J F, Mei R. Transient analysis of direct contact evaporation and condensation within packed beds[J]. International Journal of Heat and Mass Transfer, 2011, 54 : 3381–3393. DOI: 10.1016/j.ijheatmasstransfer.2011.03.048 |
| [14] | Sideman S, Hirsch G, Gat Y. Direct contact heat transfer with change of phase:Effect of the initial drop size in three-phase heat exchangers[J]. A1ChE Journal, 1965, 11(6) : 1081–1087. |
| [15] | Seetharamu K N, Battya P. Direct contact evaporation between two immiscible liquids in a spray column[J]. Journal of Heat Transfer, 1989, 111(3) : 780–785. DOI: 10.1115/1.3250751 |
 2017, Vol. 34
2017, Vol. 34





