规整填料塔目前已经广泛应用与石油化工领域。因为它具有压降低、通量大、效率高,而且持液量小的优势。同时,规整填料塔具有结构规整的特点,与板式塔相比,通过合理巧妙的设计,能使因工业化而产生的放大效应降到几乎为0[1],但是由于技术水平的限制,学术界对规整填料塔内流体的流动机理尚无定论,由于机理的不明确,限制了其进一步的发展和更新。对规整填料机理的研究具有现实的难度,因为这种填料在结构上有规整性与复杂性并存的特点,即存在各项异性,这是结构上区别于散装填料的显著特点。随着现代计算机理论和算法的进步,电算法解决工程问题已经越来越普遍。这些进步为CFD研究填料塔内的流体力学性能提供了技术支持。谷芳[2]对规整填料板表面上的液体降膜流动过程建立了三维模拟,对这一实际过程进行了研究,此法是通过与二维模型的对比,并在此基础上构建波纹板和平板的三维降膜两相流模型的基础之上进行的。陈江波[3-4]提出的三维两相流动模型中,对气液相间作用力源项(FLG)和液相表面张力源项(Fvol)对结果的影响给予重视。在他的工作中,明确阐释了规整填料特征结构单元内的润湿面积、持液量和该单元结构之分离效率于不同操作条件下的变化,并得到了气液相的速度和各个组分的浓度分布图,以直观的方式表现出气液相在模型表面的运动状态。值得注意的是,以上研究均是以规整填料内气液两相逆流流动现象做为研究背景。研究流体并流流动在当今具有非常现实的意义,例如:汽液喷射反应器及环流反应器中气液两相垂直向下或垂直向上的并流流动;真空蒸发和真空干燥系统用于排除不凝性气体并制造真空的水力喷射器的大气腿中气液两相的垂直向下并流流动;管内气液两相混合的倾斜并流流动等。随着经济发展的需要以及绿色化工概念的指导,如何能节省设备投资,降低设备占地面积已变得非常重要。并流流动能有效解决上述问题,但遗憾的是,与并流流动相关的理论研究目前非常之少,特别是并流过程中的传质过程和流体力学行为。
为了填补气液两相在规整填料中并流流动时机理研究领域的空白。本论文通过构建三维模型,应用流体力学的计算方法对简化的Mellapak350Y规整填料内的并流现象进行了研究,并通过相关实验,以验证研究成果。
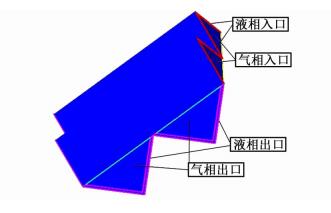
1 物理模型的建立受到当今技术条件的限制,并不能实现直接利用CFD方法模拟规整填料塔内气液两相流动的过程。主要是因为规整填料内部复杂的几何结构,使填料内部出现沟流或者溪流等比较复杂的流动形式,而不仅仅是均匀降膜流动。其次,当今计算机的算法和运算速率还不能满足这一复杂计算的需求。为解决这些不足,常用的方法是将规整填料床层的内部结构根据流体在其表面的传质特点分成4类特征单元,并对不同类型的单元分别进行CFD计算。通过比较,发现交叉特征单元,即第二特征单元在填料层中占比高达70%之上[5],与其他3种相比,比例最高。为更好的描述这一单元,本论文在其基础上构建了并流流动的CFD三维模型,如图 1。其中,把方向相反的2条三角形流道也包含在模拟区域内(以Mellapak350Y型号的板波纹规整填料的波纹为基础模型)。
|
| 图 1 规整填料三维近似物理模型的建立 Figure 1 Construction of three-dimensional physical model of structured packing |
| |
为加快计算机对模型的处理速度,在可控的模拟范围内对模型的物理结构稍作调整,假设其表面没有开孔,而且不加纹。称之为简化的Mellapak填料。
1.1 边界条件模拟规整填料内气液两相并流时的流动过程,对气液两相,共有2个进口和2个出口(见图 1)。
1.2 网格划分方法在计算之前,对模型进行网格划分。由于本论文中计算模型的几何形状非常复杂,因此采用了非结构化四面体网格进行分网。所划分的网格总数为29 474个,如图 2。

|
| 图 2 计算模型的网格 Figure 2 Grid of computational model |
| |
有文献报道[33-34]将规整填料的结构切割为4类特征单元(REU,representative elementary unit),如图 3所示,对各单元分别进行CFD模拟,而在这几类特征单元中,第2类单元,即交叉特征单元在填料中所占的份额最多。因此,本论文将采用此结构单元对气液两相的并流流动进行近似描述。

|
| 图 3 板波纹规整填料的四种典型的结构单元 Figure 3 Typical representative elementary units approximating corrugated-sheet structured packing |
| |
| 条件 | 备注 | |
| 液相进口 | 速度: |
水力直径可表示为:液相的水力直径为液膜厚度的4倍 |
| 相含率: |
||
| 湍流强度: |
||
| 速度: |
||
| 气相进口 | 相含率: |
S为规整填料波纹的斜边边长 |
| 湍流强度: |
||
| 水力直径: |
||
| 液相出口 | 取为完全发展的流动条件,同时出口压力设为1.013×105 Pa | |
| 气相出口 | ||
| 壁面 | n为垂直于壁面的向量 | |
本论文采用VOF模型,即一种追踪气液相界面模型,来模拟本研究体系中气液两相的非稳态分层流动现象。经试验证明,若利用常用的拉格朗日离散相模型或欧拉连续介质模型描述分散相都难以很好地描述整体的流动过程,究其本质,主要因为气液两相之间其实存在非常复杂的相互作用。
2.2 控制方程假设气液两相均是牛顿流体,液相不可压缩,气相是理想气体。当气液两相处于1个单元结构时,可认为两相恒温,此时,混合体系的物理性质仅为组成的函数,控制方程分列于下。
质量守恒方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0 $ | (1) |
动量守恒方程:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {p{u_i}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}{u_j}} \right) =-\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\tau ij + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial {x_i}}}\left\langle {-\rho {{u'}_i}{{u'}_j}} \right\rangle + \rho {g_i} + {F_i} \end{array} $ | (2) |
通常,对于流体的湍流行为常用标准的k-ε模型,本体系中气液均处于湍流流动状态。通过Raynal等[6]对不同湍流模型的模拟效果的比较,发现描述规整填料内流体的流动最合理的模型是RNG (Renormalization group)k-ε模型,所以本论文利用RNG k-ε模型来描述该体系的湍流行为。
湍动能k的输运方程为:
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}k} \right) = \frac{\partial }{{\partial {x_i}}}\left( {{\alpha _k}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_i}}}} \right) + {G_k}-\rho \varepsilon $ | (3) |
耗散率ε的输运方程为:
| $ \begin{array}{l} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}\varepsilon } \right) = \frac{\partial }{{\partial {x_i}}}\left( {\frac{{{\mu _{{\rm{eff}}}}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;{C_{1\varepsilon }}\frac{\varepsilon }{k}{G_k}-{C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}-{R_\varepsilon } \end{array} $ | (4) |
方程中所涉及的流体物性参数(黏度μ和密度ρ)可以与各相的体积分率建立函数关系。可通过公式(5)和(6)求得黏度和密度:
| $ \rho = {\alpha _{\rm{L}}}{\rho _{\rm{L}}} + \left( {1-{\alpha _{\rm{L}}}} \right){\rho _{\rm{G}}} $ | (5) |
| $ \mu = {\alpha _{\rm{L}}}{\mu _{\rm{L}}} + \left( {1-{\alpha _{\rm{L}}}} \right){\mu _{\rm{G}}} $ | (6) |
αL为计算单元内液相的体积分率。
在VOF法中,通过求解包含相体积分率的连续方程来完成气液两相的相界面的计算。本论文中,液相(分散相)体积分率的连续性方程为:
| $ \frac{{\partial {\alpha _{\rm{L}}}}}{{\partial t}} + {u_j} \cdot \nabla {\alpha _{\rm{L}}} = 0 $ | (7) |
气相(主相)的体积分率由式(8)得到。
| $ {\alpha _{\rm{G}}} + {\alpha _{\rm{L}}} = 1 $ | (8) |
气液两相在填料塔中的流动有其特殊性,根据其特征,本论文主要关注了以下2个动力源项的作用,分别是气液相间作用力动量源项FLG和表面张力动量源项Fvol,其中Fi为各方向的动量源项。方程如下:
| $ {F_i} = {F_{{\rm{vol}}, i}} + {F_{{\rm{LG}}, i}} $ | (9) |
表面张力在本体系中的影响非常重要,这主要是根据液相在填料塔内的特有流动形式决定的。液膜和液滴是液相在填料塔内的主要存在形式,其自上而下在塔内运动。根据表面张力的知识,液滴大小和液膜于填料表面的铺展程度都受到该力的影响,所以,模型构建的过程中,必须考虑表面张力的影响。
根据流程模拟系统Fluent的设置,可利用CSF模型对表面张力源项进行模拟(系统默认),其推导过程参见文献[7]。
最终,表面张力源项的表达形式如式(10)。
| $ {F_{{\rm{vol}}}} = {\sigma _{{\rm{LG}}}}\frac{{\rho {\kappa _{\rm{L}}}\nabla {\alpha _{\rm{L}}}}}{{\frac{1}{2}\left( {{\rho _i} + {\rho _j}} \right)}} $ | (10) |
对气液两项之间作用的影响也构建了模型。根据谷芳[2]的研究,填料塔内液相表面很容易因为即便是微小的气速而影响其表面的波动程度,这种波动对气液相间的接触面积影响较大,进而影响规整填料内的总传质扩散系数(KOGae或KOLa),最终影响传质速率。
本论文采用Hewitt[8]提出的气液相间作用力模型,其具体表达式为:
| $ {\tau _{{\rm{LG}}}} = \frac{1}{2}{\rho _{\rm{G}}}{f_{{\rm{LG}}}}\left| {{{\vec u}_{{\rm{L, }}i}}-{{\vec u}_{{\rm{G, }}i}}} \right|\left( {{{\vec u}_{{\rm{L, }}i}}-{{\vec u}_{{\rm{G, }}i}}} \right) $ | (11) |
式(11)中, fLG为气液相界面处的摩擦系数,本论文的摩擦系数采用Riazi提出的模型[9]。
| $ {f_{{\rm{LG}}}} = \left\{ \begin{array}{l} \frac{1}{{\mathit{R}{\mathit{e}_{\rm{G}}}}}\left( {\mathit{R}{\mathit{e}_{\rm{G}}} > 2000} \right)\\ \frac{{2\mathit{Re}_{\rm{G}}^{0.33}}}{{3050}}\left( {2000 < \mathit{R}{\mathit{e}_{\rm{G}}} < 4000} \right)\\ \frac{{0.08}}{{\mathit{Re}_{\rm{G}}^{0.25}}}\left( {\mathit{R}{\mathit{e}_{\rm{G}}} > 4000} \right) \end{array} \right. $ | (12) |
方程(12)描述的气液相间作用力源项只是存在于气液相界面周围的计算单元。这不同于气液单项流动区域计算单元的计算方式,因为在该计算区域并没有相间作用力源项。气液相间作用力模型在软件中一般首先需要编写用户自定义函数UDF,然后从Fluent的主控制面板中导入,这和表面张力源项的导入方式有所不同。
值得一提的是,在模型中加入相间作用力之前必须判断该计算单元内的相含率,这主要是为了确定研究的计算单元是否处于相界面周围。因为相间相互作用力的本质(两相界面的摩擦力)告诉我们,该力一般出现在两相界面附近,可是VOF模型中变量及属性均为体积平均值,且只有1个动量方程。若计算单元在液相中,FD为正,否则为负。
3 计算结果与讨论对填料塔内并流流动持液量和压降的变化情况作了研究。在该三维模型中,气液相并流流动,从填料上部的气相口进入。
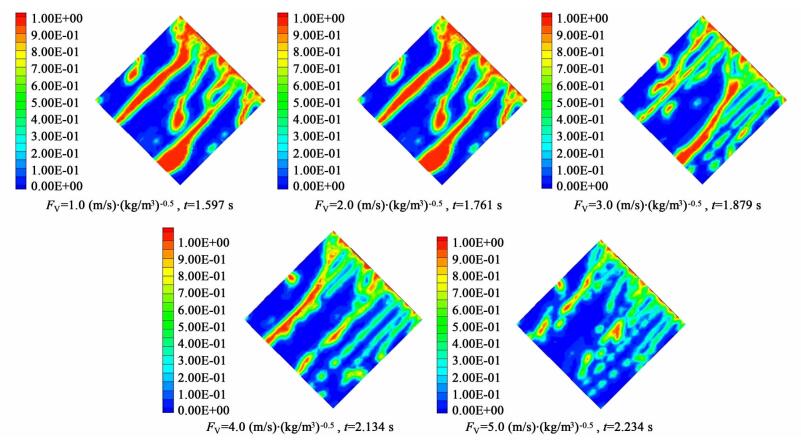
3.1 填料表面液相的流动受气相Fv因子的影响不同Fv因子[喷淋密度设定为12.286 m3·(m2·h)-1]时,填料表面的液体含有率分布如图 4所示(此时规整填料单元的流动基本达到稳定)。
|
| 图 4 填料表面液体分布受Fv因子的影响 Figure 4 Liquid distribution on the surface of the structured packing at the different Fv factors |
| |
如图 4所示,由于重力和表面张力对液相的影响不同,相比而言,前者作用力更大。这使得当液相在填料上表面形成连续液膜时,即气相Fv因子较小时,液膜下表面要宽于上表面。随着气相Fv因子的逐渐增加,液相的存在形式也随着逐渐发生变化。此时,在填料的表面,液相的存在形式是液膜和液滴。在Fv因子较小时,此时气相对液相的推动力比较小,所以流动相能形成连续的液膜;随着气速增加,气相的Fv因子增加到5及以上时,液相的存在形式有液膜转变为液滴,流动相由液相为主转变为气相和液相的混合物。随着气相的Fv因子持续提高,气体对液膜的推动力也将持续增加,最终,液相在填料的表面将很难形成连续膜。同时可以发现,流动形式主要以溪流或者沟流为主,且其在下表面的宽度均宽于上表面。
3.2 不同气相Fv因子时,压降随液相喷淋密度的变化关系研究了并流流动时填料层内的压降随气液相流速的变化情况,并将模拟值与实验值进行了对比。实验是以空气和水作为测试物系,在常压和常温下进行的并流操作,实验中的测试填料为简化的Mellapak350Y型金属板波纹填料,实验流程如图 5所示。模型选取了5个液相喷淋密度在4个气相Fv因子下的压降变化情况进行了比较验证。

|
| 图 5 试验流程图 Figure 5 Experimental procedure chart |
| |
CFD中的设置列于表 2。
| Fv因子/ [(m·s-1) ·(kg·m-3)0.5] |
CFD设置 进口流速/(m·s-1) |
喷淋密度/ [m3·(m-2·h-1)] |
CFD设置进 口流量/(L·h-1) |
| 4.0 | 3.61 | 29.44 | 120 |
| 6.0 | 5.42 | 46.67 | 190 |
| 8.0 | 7.22 | 63.81 | 260 |
| 10.0 | 9.04 | 81.09 | 330 |
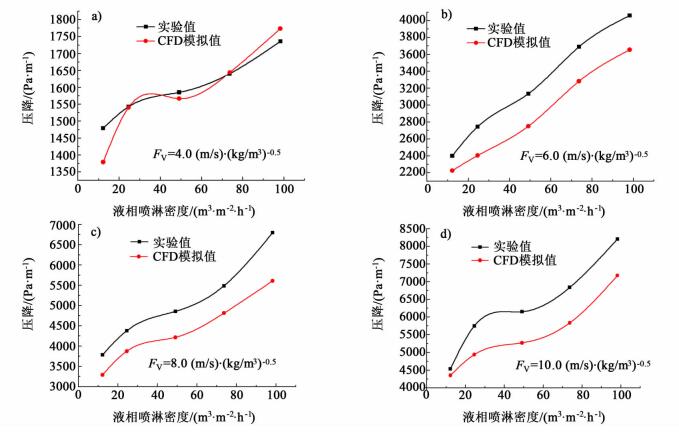
当气液两相并流流动,且气相Fv因子不同时,模型内压降和液相喷淋密度的关系见于图 6。
|
| 图 6 压降与液相喷淋密度受Fv因子的影响 Figure 6 Relationship between pressure drop and liquid spray density at the different Fv factors |
| |
从图 6中可以看出,液相中喷淋密度与压降成正相关关系,且在不同气相Fv因子时皆成立,从实验结果上看,模拟值与实验室在20%的误差范围之内,吻合效果较好。出现此现象主要是因为填料内的积液对气相流动的阻力比喷淋密度增大对气相推动的影响要大的多,使得积液的影响占据主要地位,最终导致了压降的增大;值得一提的是,在小气相Fv因子下,压降的变化随喷淋密度增大比较反常。其机理尚不明确,原因可能与大气相Fv因子时的流动机理正好相反,即液相流动对气相的推动力要比填料内液相的积液阻力大,导致压降下降,此时液相对气相的流动推动力不能忽视。由图 6可以看出,同一喷淋密度条件下,压降与气相Fv因子成正相关关系。与逆流流动的压降相比,顺流流动具有较大的优势,其压降值可以降低70%,具体数据可以通过与文献值[10]的比较得到。
3.3 不同气相Fv因子下,持液量随液相喷淋密度的变化研究了并流流动时填料层内的持液量随气液相流速的变化情况,模型选取了5个液相喷淋密度在4个气相Fv因子下的压降变化情况,并将模拟值与实验值进行了对比。边界条件设定如表 2。
当气液两相并流流动,且气相Fv因子不同时,模型内持液量和液相喷淋密度的关系见于图 7。

|
| 图 7 持液量与液相喷淋密度受Fv因子的影响 Figure 7 Relationship between liquid holdup and liquid spray density at the different Fv factors |
| |
从图 7中可以看出,体系的持液量与液相的喷淋密度呈现正相关关系,且在不同的气相Fv因子时都呈现相同的规律。出现这种情况的内在原因是喷淋密度的增大使得填料层的积液增加,但前提是气相的速度一定。由于为该物理过程构建的计算机模型前期经过简化,且该试验的宏观因素可能造成一定的不确定性,使得模拟结果与实验值存在一定的允许误差,但是在实验值与计算值在变化趋势上式一致的。如图 7所示,由于气相流动对液相有推动作用,当气相Fv因子的增大时,即气相流量增大时,填料层的液相持液量明显降低(在同一喷淋密度条件下)。这一现象明显区别于逆流流动过程,在逆流流动过程中,如果体系的操作条件在载点以下,填料层的持液量随气相Fv因子增大变化较小[11],并流时,不会出现这一现象。且与逆流流动相比[12],并流过程的填料层持液量下降达50%之多。
4 结论研究了板波纹规整填料内部气液两相的并流流动现象。通过对实体结构内部的简化,用流体力学软件构建了简化的Mellapak350Y规整填料的三维立体模型。通过该模型,对气液并流流动时的持液量和压降进行了研究,通过相关实验验证了模型的准确性,且对气液并流流动在不同气相Fv因子条件下填料表面的液体分布做了研究,给出其分布图;并提出了并流流动的压降和持液量的模拟计算方法,通过实验验证发现计算结果与实验值吻合良好,与逆流流动相比,并流流动的压降下降近70%,持液量下降50%左右;小气相Fv因子的并流流动中,压降和液相喷淋密度成反比例关系;持液量随着气相Fv因子的增大而减小。
加强了对规整填料内流体流动机理的认识,从而为规整填料的进一步更新和发展提供了较好的分析方法。
| [1] |
张鹏, 刘春江, 成弘, 等. 规整填料塔内流体流动研究进展及展望[J].
化学工程, 2001, 29(3) : 66–70.
Zhang Peng, Liu Chunjiang, Cheng Hong, et al. Progress in the studies on fluid flow in structured packing tower and its prospect[J]. Chemical Industry and Engineering, 2001, 29(3) : 66–70. |
| [2] | Gu F, Liu C, Yuan X, et al. CFD simulation of liquid film flow on inclined plates[J]. Chem Eng Technol, 2004, 27(10) : 1099–1104. DOI: 10.1002/(ISSN)1521-4125 |
| [3] | 陈江波.高压下规整填料塔的计算传递及传质性能[D].天津:天津大学, 2006 Chen Jiangbo. Numerical and experimental study of transport phenomena in a structured packed column at high pressure[D]. Tianjin:Tianjin University, 2006(in Chinese) http://www.doc88.com/p-705867592296.html |
| [4] |
陈江波, 刘春江. 计算流体力学方法模拟规整填料塔内流体流动行为的研究进展[J].
石油化工, 2007, 36(9) : 962–965.
Chen Jiangbo, Liu Chunjiang. Progress of simulation of fluid flow behavior in structured packed column by computational fluid dynamics[J]. Petrochemical Technology, 2007, 36(9) : 962–965. |
| [5] | Petre C F, Larachi F, Iliuta I, et al. Pressure drop through structured packings:Breakdown into the contributing mechanisms by CFD modeling[J]. Chemical Engineering Science, 2003, 58 : 163–177. DOI: 10.1016/S0009-2509(02)00473-6 |
| [6] | Raynal L, Boyer C, Ballaguet J P. Liquid holdup and pressure drop determination in structured packing with CFD simulations[J]. Canadian Journal of Chemical Engineering, 2008, 82(5) : 871–879. DOI: 10.1002/cjce.5450820502 |
| [7] | Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension[J]. J Comput Phys, 1992, 100 : 335–354. DOI: 10.1016/0021-9991(92)90240-Y |
| [8] | Bird B, Stewart W E, Lightfoot E N. Transport phenomena[M]. New York: John Wiley & Sons, Inc, 2002 . |
| [9] | Riazi M R, Faghri A. Effect of interfacial drag on gas absorption with chemical reaction in a vertical tube[J]. AIChE J, 1986, 32(4) : 696–699. DOI: 10.1002/(ISSN)1547-5905 |
| [10] | 王树楹. 现代填料塔技术指南[M]. 北京: 中国石化出版社, 1998 |
| [11] | 董谊仁, 裘俊红, 侯章德. 现代填料塔技术(四)填料塔的流体力学和传质(上)[J]. 化工生产与技术, 1997(1) : 18–28. |
| [12] |
谷芳, 刘春江, 袁希钢, 等. 板波纹规整填料液相分布模型[J].
天津大学学报:自然科学与工程技术版, 2005, 38(7) : 586–591.
Gu Fang, Liu Chunjiang, Yuan Xigang, et al. Liquid distribution model for sheet corrugated structured packing[J]. Journal of Tianjin University, 2005, 38(7) : 586–591. |
 2017, Vol. 34
2017, Vol. 34





