板翅式换热器作为一种紧凑式换热器,具有高比表面积、高效性的优点[1],广泛应用于航天、空分、汽车等领域。翅片的类型主要包括平直、锯齿、波纹、百叶窗等;其中平直翅片具有低压降的特点,被广泛应用于对压降有特殊要求的场合[2]。
Kays and London[3]系统性地研究了各种翅片的性能;董军启[4]研究了平直翅片的性能和几何参数对性能的影响。传统的实验测定方法费事费力,效率低;而CFD数值模拟方法高效,研究者广泛采用此方法研究平直翅片性能[5-9]。Bala[6]在忽略翅片效率的条件下,回归了层流和湍流区域内j、f因子与Re、几何结构参数间的关联式。Wang[7]建立了平直和锯齿形翅片在层流区域的计算模型;Zhu[8]根据局部Nu的变化得到了进口段长度,比较了在层流区域内平直、锯齿、波纹和开孔翅片的性能。
公开发表的文章中多研究层流区域翅片性能,而实际工业装置中换热器多工作在湍流区域;同时翅片与上(下)板间存在温差,需要考虑翅片的纵向导热。本研究主要的工作是在考虑翅片纵向导热的条件下,用CFD的方法建立准确模拟平直翅片在湍流区域性能的计算模型,并通过分析局部温度场和速度场对翅片结构进行改进;以期为平直翅片设计、优化提供依据,为其他类型翅片在湍流区域的数值模拟提供参考。
1 数值模型的建立 1.1 数值模型换热器和翅片通道尺寸分别在米和毫米数量级;本研究只计算单个通道[5, 9],结合相应的边界条件来模拟整个换热器。平直翅片示意图见图 1。

|
| 图 1 平直翅片结构示意图 Figure 1 Structure of plain fin |
| |
根据Wang[7]、祝银海[9]的研究工作,采用周期流模型计算翅片性能。垂直于x轴方向的前后两个面设为周期流边界,进口温度300 K;侧面为对称边界;上下壁面为310 K等温壁面,流固接触面为耦合壁面边界。流体在平直翅片通道内的流动行为与Ali[10]中两平板间的流动相似,因此当Re<2000时采用层流模型,Re≥2000时采用湍流模型。在湍流区域,为准确求解主要受黏性力影响的近壁面区域,采用低雷诺数湍流模型[11]。在平直翅片通道中,流体流动各向同性,Lam and Bremhorst[12]模型是在标准k-ε模型基础上修改的一种低雷诺数湍流模型,与其他修改方式相比更适用于平直翅片通道中的流动[13],因此采用此低雷诺数湍流模型。为了满足此模型的使用条件,对壁面区域网格加密使y+<1;并对网格进行无关性验证。计算模型和网格示意图见图 2。

|
| 图 2 平直翅片计算模型和网格示意图 Figure 2 Computation model and grid system |
| |
由数值计算得到的数据,分别通过计算得到翅片的摩擦因子f和传热因子j。
j因子定义为:
| $ j = \frac{h}{{\rho u{C_p}}}\mathit{P}{\mathit{r}^{\frac{2}{3}}} $ | (1) |
其中,Cp为定压比热容,Pr为普朗特数,h为换热系数,u为空气进口速度,ρ为空气密度。
f因子定义为:
| $ f = \frac{{\Delta P}}{{2\rho {u^2}}}\frac{{{D_{\rm{e}}}}}{L} $ | (2) |
其中De为水力学直径,△P为空气侧气体压降,L为翅片长度。
1.2 湍流普朗特数为了简便,采用二维流动来解释湍流普兰特数(对于三维流动同样适用),详细信息见Kays[14]、Fluent Inc[15]和Srinivasan[16]。假设流体物性保持不变,没有黏度耗散。
动量方程:
| $ {u_x}\frac{{\partial {u_x}}}{{\partial x}} + {u_y}\frac{{\partial {u_x}}}{{\partial y}} + \frac{1}{\rho }\frac{{{\rm{d}}P}}{{{\rm{d}}x}} = \frac{\partial }{{\partial y}}\left( {v\frac{{\partial {u_x}}}{{\partial y}}-\overline {{{u'}_x}{{u'}_y}} } \right) $ | (3) |
能量方程:
| $ {u_x}\frac{{\partial T}}{{\partial x}} + {u_y}\frac{{\partial T}}{{\partial y}} = \frac{\partial }{{\partial y}}\left( {a\frac{{\partial T}}{{\partial y}}-\overline {T'{{u'}_y}} } \right) $ | (4) |
其中v为动力黏度;a为热扩散系数。
根据湍流扩散系数的定义有:
| $ \overline {{{u'}_x}{{u'}_y}} =-{v_{\rm{t}}}\left( {\frac{{\partial {u_x}}}{{\partial y}}} \right) $ | (5) |
| $ \overline {T'{{u'}_y}} =-{a_{\rm{t}}}\left( {\frac{{\partial T}}{{\partial y}}} \right) $ | (6) |
定义湍流普朗特数为:
| $ \mathit{P}{\mathit{r}_{\rm{t}}} = \frac{{{v_{\rm{t}}}}}{{{a_{\rm{t}}}}} $ | (7) |
代入方程(4),重新整理得:
| $ {u_x}\frac{{\partial T}}{{\partial x}} + {u_y}\frac{{\partial T}}{{\partial y}} = \frac{\partial }{{\partial y}}\left\{ {v\left[{\frac{1}{{\mathit{Pr}}} + \frac{{{v_{\rm{t}}}/v}}{{\mathit{P}{\mathit{r}_{\rm{t}}}}}} \right]\frac{{\partial T}}{{\partial y}}} \right\} $ | (8) |
求解动量方程,可以得到任意位置的ux,uy,vt,只需知道Prt数就可以求解方程(8)。
Srinivasan[16]指出湍流普朗特数主要与流体的普朗特数、壁面距离有关。但在广泛使用的计算流体力学FLUENT软件中湍流普朗特数设置为常量(0.85),忽略了流体普朗特数、壁面距离对其影响。本模拟中工作介质为空气,普朗特数为0.74与Kim and Moin[17]用DNS方法研究的流体普朗特数(0.71)接近。在湍流区域(Re≥2000):根据Kays[14]、Kim and Moin[17]的工作,经验关联式(9)与Kim and Moin[17]直接数值模拟的结果相吻合;且与其他模型相比,方程(9)与实验结果更吻合。因此采用此湍流普朗特数模型,并用UDF (用户自定义函数)方法编译。
| $ \mathit{P}{\mathit{r}_{\rm{t}}} = \frac{{0.7}}{{\left( {\frac{{{v_{\rm{t}}}}}{v}} \right)\mathit{Pr}}} + 0.85 $ | (9) |
在文献[3]中,实验芯体是错流式热交换器,尺寸为222 mm×248 mm;空气一侧被加热,蒸汽一侧被冷凝。空气侧流量由孔板流量计测定;下游截面有27个温度测点以得到准确的平均温度,热电偶系统精度±0.11 ℃;实验段压差由倾斜式微压计测定。蒸汽侧供给精确控制的低过热蒸汽,大约4倍于冷凝量的蒸汽,防止形成较大的膜状冷凝热阻。两侧能量平衡偏差小于3%。结合以上的实验描述和多位研究者[5-7]引用此实验数据,说明实验数据是可靠的;因此本研究将计算结果与该实验数据进行对比。
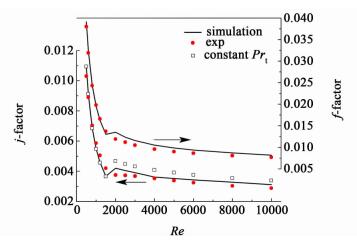
图 3中将文献[3]中代号为11.11的平直翅片计算值与实验值进行对比,同时比较了采用Prt模型[方程(9)]与默认常量(0.85)的j因子。其中11.11平直翅片参数如下:翅片间距Fp=2.286 mm,翅片高度Fh=12.19 mm,翅片厚度δ=0.203 mm。在湍流区域,采用默认Prt为0.85的计算j因子与实验结果的平均绝对误差为17.94%,而采用Prt模型[方程(9)]的j因子平均绝对误差为6.93%。通过以上对比,说明Prt模型能更准确预测j因子。
|
| 图 3 计算结果与实验结果对比 Figure 3 Validate numerical model with experimental work |
| |
计算j和f因子与实验结果的平均绝对误差分别为6.72%和6.47%。在雷诺数为2 000左右误差最大,分别为11.90%和13.50%,因为在雷诺数为2 000区域流动处于过渡流状态,层流和湍流模型都不能很好预测此域内的流动状态。通过与实验数据对比,说明计算模型能准确预测平直翅片性能。
2.2 结果与讨论在图 4和图 5中分别给出了在x=0截面处(见图 2)代号为11.11平直翅片沿y轴方向的温度和局部传热系数分布曲线。翅片中心处温度最低,且随着雷诺数的增大而降低;雷诺数为500时,温度变化趋势平缓;雷诺数为8 000时,翅片中心处温度迅速降低。雷诺数为500和8 000时,翅片中心处与进口流体的温差比上下板与进口流体的温差分别低5%和18%;因此在用CFD模拟翅片通道内的换热情况时需要考虑翅片的纵向导热,不能忽略翅片与上下板之间的温差。

|
| 图 4 翅片沿y轴方向温度分布 Figure 4 Temperature distribution along y axis |
| |
|
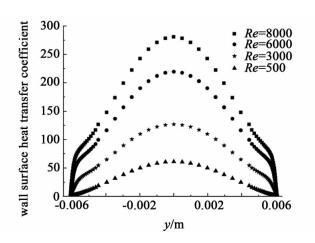
| 图 5 翅片表面沿y轴方向传热系数分布 Figure 5 Surface heat transfer coefficient distribution along y axis |
| |
在图 5中翅片表面传热系数随着雷诺数的增大而增大;翅片表面局部对流传热系数分布不均匀且不均匀性随着雷诺数的增大而增大。在翅片中心处局部传热系数最大(图 6中B区域);越靠近翅片与上(下)板接触区域(图 6中A区域)局部传热系数越低。在雷诺数为500时,翅片表面传热系数变化平缓;随着雷诺数增大,对流换热系数迅速增大。
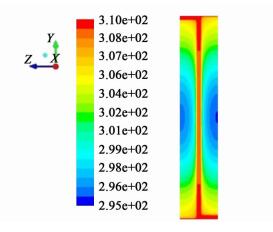
图 6和图 7中分别给出雷诺数为8 000时,x=0截面处的速度和温度分布图。翅片与上下板接触区域(A区域)速度和温度边界层厚度比翅片中间区域(B区域)厚,这是因为A区域的流体同时受到翅片和上(下)板施加的阻力,而B区域只受到翅片施加的阻力。因此在A区域的流体流动不畅,边界层相对较厚,局部换热系数与B区域相比相对较低。

|
| 图 6 速度分布图Re=8000 Figure 6 Velocity distribution at Re=8000 |
| |
|
| 图 7 温度分布图Re=8000 Figure 7 Temperature distribution at Re=8000 |
| |
为强化翅片与上(下)板接触区域的传热,将11.11平直翅片间隔的切除一部分,具体模型见图 8。

|
| 图 8 新型翅片示意图 Figure 8 A schematic view of new fin |
| |
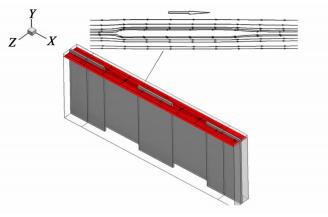
图 9中给出新型翅片在Re=6000,y=0.0056 m截面的流线图。
|
| 图 9 流场分布图 Figure 9 Velocity distribution of new fin at Re=6000 |
| |
从图 9中可以看出,流动与锯齿形翅片相似;由于间隔切除了部分翅片,周期性破坏了接触区域的边界层,强化了传热。
图 10中给出了j/j0和f/f0随雷诺数的变化,其中j、f;j0、f0分别代表新型翅片、平直翅片的j和f因子。雷诺数为500~6 000区间内,新型翅片的j因子与平直翅片相比增大2.76%~12.44%。f因子变化受2个因素影响:1)由于周期性破坏接触区域的边界层,f因子增大;2)由于切除了部分翅片,翅片对流体施加阻力减少。在低雷诺数区域,后者为主要因素,f因子降低;随着雷诺数增大,前者成为主要因素,f因子增大。在层流区域,新型翅片综合性能最好,说明此翅片最适用于层流区域。

|
| 图 10 新型翅片与平直翅片性能对比 Figure 10 Performance comparison between new and plain fin |
| |
用CFD方法建立了简单、准确计算平直翅片在层流和湍流区域性能的数值模型。该模型的计算j和f因子与实验结果的平均绝对误差分别为6.72%和6.47%;说明模型能准确预测平直翅片性能。结合局部速度、温度分布场和翅片表面传热系数分布图,对翅片结构进行优化,提高翅片整体性能,主要结论包括:
1)在湍流区域使用Lam-Bremhorst[12]低雷诺数湍流模型求解主要受黏性力影响的近壁面区域并结合湍流普朗特数模型代替默认的常量(0.85)能更准确预测翅片的性能。
2)翅片中心处温度最低,且随着雷诺数增大而降低。翅片中心处与进口流体温差比上(下)板与进口流体温差低5%~18%;因此在计算翅片性能时,不能忽略翅片纵向导热。
3)翅片与上(下)板接触区域同时受翅片和上(下)板壁面施加阻力,对流传热系数相对较低;间隔切除接触区域,破坏流体边界层的形成,能提高翅片综合性能;其中j因子增大2.76%~12.44%而f因子保持不变。
| [1] |
陈长青, 沈裕浩.
低温换热器[M]. 北京: 机械工业出版社, 1993 Chen Changqing, Shen Yuhao. Cryogenic heat exchanger[M]. Beijing: Machinery Industry Press, 1993 . |
| [2] | 董军启.车辆冷却系统空气侧特性研究[D].上海:上海交通大学, 2008 Dong Junqi. Research on air side flow and heat transfer character of vehicle cooling systems[D]. Shanghai:Shanghai Jiaotong University, 2008(in Chinese) |
| [3] | 凯斯W M, 伦敦A L著.紧凑式热交换器[M].宣益民, 张厚雷译.北京:科学出版社, 1997 Kays W M, London A L. Compact heat exchangers[M]. Xuan Yimin, Zhang Houlei Trans. Beijing:Science Press, 1997(in Chinese) |
| [4] |
董军启, 陈江平, 袁庆丰. 板翅换热器平直翅片的传热与阻力性能试验[J].
农业机械学报, 2007, 38(8) : 53–56.
Dong Junqi, Chen Jiangping, Yuan Qingfeng. Flow and heat transfer on compact smooth fin surfaces[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(8) : 53–56. |
| [5] |
文键, 李亚梅, 王斯民, 等. 板翅式换热器平直翅片表面流动及传热特性[J].
化学工程, 2012(10) : 25–28.
Wen Jian, Li Yamei, Wang Simin. Fluid flow and heat transfer characteristics in plain fins of plate-fin heat exchanger[J]. Chemical Engineering (China), 2012(10) : 25–28. |
| [6] | Rao R B S, Ranganath G, Ranganayakulu C. Development of Colburn 'j' factor and fanning friction factor 'f' correlations for compact heat exchanger plain fins by using CFD[J]. Heat Mass Transfer, 2013, 49(7) : 991–1000. DOI: 10.1007/s00231-013-1140-0 |
| [7] | Wang Y, Dong Q, Liu M, et al. Numerical study on plate-fin heat exchangers with plain fins and serrated fins at low Reynolds number[J]. Chemical Engineering and Technology, 2009, 32(8) : 1219–1226. DOI: 10.1002/ceat.v32:8 |
| [8] | Zhu Y, Li Y. Three-Dimensional numerical simulation on the laminar flow and heat transfer in four basic fins of plate-fin heat exchangers[J]. Journal of Heat Transfer, 2008, 130 : 1–8. |
| [9] |
祝银海, 厉彦忠. 板翅式换热器翅片通道中流体流动与传热的计算流体力学模拟[J].
化工学报, 2006, 57(5) : 1102–1106.
Zhu Yinhai, Li Yanzhong. CFD simulation of fluid flow and heat transfer in channels of plate-fin heat exchangers[J]. Journal of Chemical Industry and Engineering (China), 2006, 57(5) : 1102–1106. |
| [10] | Ali M M. Experiments on convective heat transfer in corrugated channels[J]. Experimental Heat Transfer, 1992, 5(3) : 175–193. DOI: 10.1080/08916159208946440 |
| [11] | Virendra P, Wolfgang R, Georg S. Turbulence models for near-wall and low Reynolds number flows:A review[J]. AIAA Journal, 1985, 23(9) : 1308–1319. DOI: 10.2514/3.9086 |
| [12] | Lam C K G, Sharmahorst K A. Modified form of the k-ε model for predicting wall turbulence[J]. Journal of Fluids Engineering, 1981, 103 : 456–460. DOI: 10.1115/1.3240815 |
| [13] | Cokljat D, Kim S E, Iaccarino G, et al.A comparative assessment of the V2F model for recirculating flows[C]//41st Aerospace Sciences Meeting and Exhibit, 2003 |
| [14] | Kays W M. Turbulent Prandtl number-Where are we?[J]. Journal of Heat Transfer, 1994, 116(2) : 284–295. DOI: 10.1115/1.2911398 |
| [15] | Fluent Inc.FLUENT 6.3 User's Guide[M]. 2006 |
| [16] | Srinivasan C, Papavassiliou D V. Prediction of the turbulent Prandtl number in wall flows with Lagrangian simulations[J]. Ind Eng Chem Res, 2011, 50(15) : 8881–8891. DOI: 10.1021/ie1019497 |
| [17] | Kim J, Moin P. Transport of passive scalars in a turbulent channel flow[C]//Proceedings of Six International Symposium on Turbulence Shear Flows, Beilin-Heidelberg:Spring-Verlag, 1987:85-96 |
| [18] | Churchill S W. AIChE institute lecture:Progress in the thermal sciences[J]. AIChE, 2000, 46(9) : 1704–1722. DOI: 10.1002/(ISSN)1547-5905 |
 2017, Vol. 34
2017, Vol. 34





