2. 化学化工协同创新中心, 天津 300072 ;
3. 化学工程联合国家重点实验室, 天津 300072 ;
4. 天津市膜科学与海水淡化重点实验室, 天津 300072
2. Collaborative Innovation Center of Chemical Science and Engineering(Tianjin), Tianjin 300072, China ;
3. State Key Laboratory of Chemical Engineering, Tianjin 300072, China ;
4. Tianjin Key Laboratory of Membrane Science and Desalination Technology, Tianjin 300072, China
膜蒸馏分离纯化技术可以利用低品位热源如烟道气、废热、太阳能等作为原料加热的热源, 因此与传统的反渗透、蒸馏等分离技术相比膜蒸馏技术更具优势[1]。在膜蒸馏过程中, 疏水性的高分子聚合多孔膜并不直接参与分离, 只是作为将料液和渗透液(蒸汽)分隔开的屏障, 而过程的选择性完全取决于热料液在膜表面的汽-液相平衡关系, 属于热分离过程。膜蒸馏主要有4种操作方式:直接接触式(DCMD)、气隙式(AGMD)、气扫式(SGMD)和减压膜蒸馏(VMD), 其中具有较高的膜通量且渗透侧极化效应可以忽略的减压膜蒸馏得到了较为广泛的研究和应用, 比如陈迅等[2]开展了VMD用于浓缩脱硫液的研究, 刘学晶等[3]研究了VMD过程中的热量回收利用, 吕双江[4]对减压多效膜蒸馏过程进行了研究。
随着CFD(Computational Fluid Dynamics)技术的发展和在热量、质量传递方面的普遍应用, 国内外不少研究者将CFD模拟与膜蒸馏过程相结合用于研究膜蒸馏过程的传递现象和流场分布情况等。例如, 朱春英等[5]通过数值模拟研究分析了膜材料参数对中空纤维减压膜蒸馏过程通量的影响, 探讨了纤维膜丝长度、厚度以及膜丝内径、曲折因子等对膜性能的影响, 对减压膜蒸馏过程中膜的选取提供了理论参考;刘典[6]模拟分析了操作条件对膜通量的影响, 结果表明进料温度、流速以及真空度的提高有利于提高膜通量, 而高的进料浓度将降低膜通量;Zhang等[7]通过CFD模拟软件研究了中空纤维减压膜蒸馏用于NaCl水溶液浓缩的过程, 讨论了纤维内腔盐浓度的变化和跨膜传质蒸汽的分布及变化规律, 结果表明减压膜蒸馏过程中压力梯度和气相分率梯度主要存在膜层中, 而相变和温度梯度主要在膜表面发生。这些研究加深了对膜蒸馏过程的理解和认识, 对膜蒸馏的应用有促进作用, 但是朱春英、刘典等的研究只是对膜过程的宏观通量进行模拟, 缺乏对膜蒸馏过程的微观现象的研究;而Tang等的研究虽然是从微观层面上对膜蒸馏过程进行了描述, 但是其研究主要侧重于对过程现象的描述, 缺乏直观数字化的研究资料, 如膜表面不同位置处的速度、温度分布规律, 热量和质量传递特性及分布规律, 操作条件对这些参数分布的影响等, 这些因素是直接影响膜蒸馏过程的重要参数, 了解其分布规律有利于提出新的膜通量强化方向, 提高膜蒸馏性能, 因此很有必要对其进行深入研究。
本研究采用通用CFD软件FLUENT对错流式减压膜蒸馏过程进行了数值模拟研究, 以单根中空纤维膜为研究对象, 对错流流场中膜表面不同流动位置处的流动速度和温度分布以及热量和质量传递速率进行了研究, 并考察了不同料液流速、冷侧真空度对热量和质量传递参数分布规律的影响。
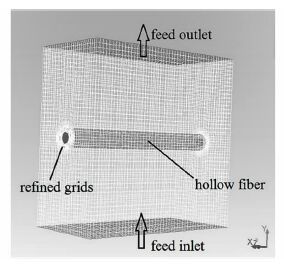
1 计算模型 1.1 模型简介为探究膜表面不同位置处的热量和质量传递特征, 本研究只对单根中空纤维膜丝的减压膜蒸馏过程进行研究, 建立的计算模型如图 1所示。热的料液沿着Y轴方向流动, 与纤维膜丝长度方向(X轴)正交, 因此流动方式为错流式。与实际过程相比, 该计算模型进行了部分合理简化:1) 进出口简化为整个平面, 忽略进出口处的突然扩大和突然缩小对流体流动的影响, 模拟模型相当于在膜组件中部位置某纤维膜的减压膜蒸馏过程;2) 流体在组件中的流动属于完全发展的湍流流动;3) 进料液为纯水, 不含盐成分的扩散和传递过程;4) 液体为不可压缩黏性流体, 在计算温度范围内, 其密度恒定。
|
| 图 1 计算模型及计算网格 Figure 1 Calculation model and grids |
| |
对上述建立的三维计算模型进行离散化处理, 采用ICEM软件对计算域进行网格划分。为了捕捉膜表面参数变化的微观特征值, 对膜表面处的计算网格进行了加密处理(图 1所示)。
1.2 流场模拟方程对不可压缩的黏性流体, 可以用纳维-斯托克斯方程(Navier-Stokes equations)来描述其中流体质点的运动规律。在直角坐标系中, 流体的质量守恒方程、动量守恒方程和能量方程描述如下:
质量方程:
| $\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0$ | (1) |
动量方程:
X方向
| $\rho \frac{{\partial u}}{{\partial t}} + \rho \nabla \cdot\left( {uV} \right) = - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} + {f_x}$ | (2) |
Y方向
| $\rho \frac{\partial v}{\partial t}+\rho \nabla \cdot \left( vV \right)=-\frac{\partial p}{\partial y}+\frac{\partial {{\tau }_{xy}}}{\partial x}+\frac{\partial {{\tau }_{yy}}}{\partial y}+\frac{\partial {{\tau }_{zy}}}{\partial z}+{{f}_{y}}$ | (3) |
Z方向
| $\rho \frac{\partial w}{\partial t}+\rho \nabla \cdot \left( wV \right)=-\frac{\partial p}{\partial z}+\frac{\partial {{\tau }_{xz}}}{\partial x}+\frac{\partial {{\tau }_{yz}}}{\partial y}+\frac{\partial {{\tau }_{zz}}}{\partial z}+{{f}_{z}}$ | (4) |
能量方程:
| $\frac{\partial T}{\partial t}+{{u}_{x}}\frac{\partial T}{\partial x}+{{u}_{y}}\frac{\partial T}{\partial y}+{{u}_{z}}\frac{\partial T}{\partial z}=\alpha \left( \frac{{{\partial }^{2}}T}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{z}^{2}}} \right)$ | (5) |
式(1) ~(5) 中, ρ为流体密度, u、v、w分别为流体在x、y、z方向的速度, t为时间, T为温度, fx、fy、fz分别为重力(质量力)在x、y、z方向上的分量, α=k/ρCv流体热扩散系数。
1.3 VMD传质模型在膜蒸馏过程中, 液态水在膜表面发生相变转化为气态并通过膜孔道传递到渗透侧, 本研究中采用尘气模型(Dust-Gas Model)来计算膜表面的蒸发速率。对单组分蒸发扩散过程其模型方程可表示为:
| $\frac{N}{{{D}^{eff}}_{k}}=-\frac{1}{RT}\left( \nabla {{P}_{v}}+\nabla {{P}_{v}}\frac{kP}{{{D}^{eff}}_{k}\mu } \right)$ | (6) |
式(6) 中, N为气体摩尔通量, μ为气体黏度, k为渗透系数。有效努森扩散系数Dkeff可根据膜材料参数按式(7) 进行计算:
| ${{D}^{eff}}_{k}=\frac{2\varepsilon {{r}_{g}}}{3\tau \delta }\sqrt{\frac{8RT}{\pi M}}$ | (7) |
式(7) 表明, 气体在微小孔道内的扩散不仅与孔道的平均孔径和曲折因子有关, 且和多孔材料的开孔率以及膜材料厚度有关。式(7) 中R为气体常数, M为水的摩尔质量。
VMD的传质推动力可由式(8) 计算:
| $\Delta {{P}_{v}}={{P}_{v}}\left( T \right)-{{P}_{p}}$ | (8) |
式(8) 中Pp是渗透侧的绝对压力, Pv(T)为温度T下的挥发性组分的饱和蒸汽压, 当水为挥发性组分时可由Antoine公式计算:
| ${{P}_{v}}\left( T \right)={{P}^{*}}_{water}=\text{exp}\left( 23.238-\frac{3841}{T-45} \right)$ | (9) |
因此纯水作为料液的VMD过程推动力可以表示为式(10) 。
| $\Delta {{P}_{v}}={{P}^{*}}_{water}-{{P}_{p}}$ | (10) |
在VMD的渗透侧是真空状态, 导热热阻很高, 因此和一般的膜蒸馏过程相比热传导作用可以忽略。VMD过程的热量传递主要是扩散的气体分子携带的潜热穿过膜孔传递到冷侧, 所以VMD总传热量:
| $Q=热侧边界层传热量\text{ }{{Q}_{f}}=跨膜传热总量{{Q}_{m}}$ | (11) |
由料液主体向膜表面边界层传热量与一般MD过程相同, 可以由式(2) ~(8) 计算得到:
| ${{Q}_{f}}={{h}_{f}}({{T}_{fb}}-{{T}_{fm}})$ | (12) |
其中, hf为对流传热系数, Tfb和Tfm分别为料液主体和膜表面的温度。
跨膜传热量因忽略了热传导作用, 因此VMD传热总量即为潜热传递量:
| $Q={{Q}_{m}}={{Q}_{v}}={{J}_{v}}{{H}_{r}}$ | (13) |
式(13) 中, Jv为跨膜传质通量, Hr为水蒸发的相变焓。
在膜组件内部, 流场温度随料液所在的位置而发生变化, 虽然整个过程达到稳态, 但是在微观上各处的温度随时间和流动状态不断发生变化。料液参数如黏度、密度、热导率等均为温度的函数, 为了更贴近实际操作过程, 在模拟中采用线性拟合的方式将黏度、密度、导热率等参数回归为温度的函数, 带入数值模拟模型中进行模拟计算。
由式(11) 、(12) 和(13) 可知, VMD过程中热侧膜表面边界层内的对流传热系数可由式(14) 计算得到。
| ${{h}_{f}}=\frac{{{J}_{v}}{{H}_{r}}}{{{T}_{fb}}-{{T}_{fm}}}$ | (14) |
中空纤维管长度为100 mm, 内径0.6 mm, 外径1.0 mm, 即纤维膜壁厚0.2 mm。计算域为宽(Z轴)40 mm, 高度(流动方向, Y轴)50 mm。基于真实中空纤维膜参数, 计算中膜孔隙率为0.55, 膜平均孔径0.2 μm。模型采用直角坐标系, 坐标原点为纤维中心处。
中空纤维膜外侧为水溶液, 在纤维内侧加载负压, 料液主体流动方向与纤维长度方向相垂直。
2.2 计算设置建立计算模型并进行网格划分后导入计算软件FLUENT中, 定义速度进口和压力出口边界条件, 设定中空纤维膜为多孔介质, 计算采用SIMPLE算法, 标准湍流双方程模型, 一阶离散格式求解。假设膜蒸馏过程达到稳态, 即膜表面参数不随时间变化, 只与位置有关。
为实现膜蒸馏过程中的相变和热量转移过程, 根据膜蒸馏过程特点和方程(6) ~(13) 编写了用户自定义程序(UDF), 在计算过程中调用UDF中的各项DEFINE宏来实现气液转化过程和该过程产生的潜热转移。
2.3 模型验证在本模拟计算中研究的是单根纤维膜表面微观层面的热质传递参数分布及变化规律, 而目前还没有仪器或设备能够对这些参数进行直接测量。因此本研究中通过测量具有相同膜材料参数的膜组件在相同实验条件下的膜通量对所建立的三维模拟计算模型进行科学性和客观性的间接验证, 增加模拟研究的可信度和参考价值。膜组件设计中增加了纤维与纤维之间的前后距离和左右距离以及纤维膜与膜组件壁面之间的距离, 以降低纤维膜之间的相互影响和组件壁面对纤维膜的影响;同时增加单层纤维根数(62根)以减少膜丝层数(8层), 降低流动过程中温度降对实验的影响。模组件参数如表 1所示。
| 项目 | 参数 |
| 纤维有效长度/mm | 100 |
| 纤维总层数/层 | 8 |
| 单层纤维数/个 | 62 |
| 组件总纤维数/个 | 496 |
| 有效膜面积(基于内径)/m2 | 0.09307 |
| 有效膜面积(基于外径)/m2 | 0.15512 |
| 操作方式 | 错流式 |
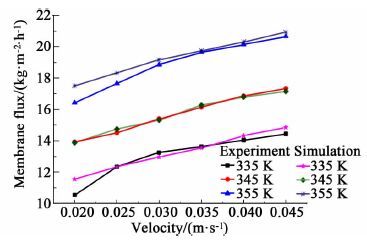
设置模型进口速度和实验操作中速度一致, 其它条件参数与实验中相同, 验证不同料液流速下计算膜通量是否与实验一致。模拟计算结果和实验结果对比如图 2所示。
由图 2中可知, 在不同的料液流速下, VMD模型的计算膜通量和实验所得的膜通量基本一致, 不同操作条件下的通量曲线变化趋势相同。这说明所建立的计算模型能够科学客观的反映实验过程, 可以进行进一步研究分析。
|
| 图 2 不同进口速度下实验值与模拟通量对比(真空度0.065 MPa) Figure 2 Comparison of membrane flux between experiments and simulations at different bulk velocity (vacuum degree at 0.065 MPa) |
| |
为了方便研究和对结果进行描述, 在纤维膜横截面上根据相位角大小对纤维管表面进行划分, 定义在重力方向的最低点为起始位置, 即相位角为0°, 按顺时针方向旋转到重力方向的最高点为180°。当相位角为90°或270°时, 该处的膜表面处于纤维的左右两侧;当相位角为0°或者360°时, 局部膜表面处于纤维管的前侧;相位角为180°时, 局部膜表面处于纤维管的后侧。具体说明如图 3所示。

|
| 图 3 环纤维表面相位角 Figure 3 Phase-angle around hollow fiber surface |
| |
由于纤维左侧(相位角从0°到180°)和右侧(相位角从180°到360°)的参数值对称分布, 本研究选取左侧参数分布值进行分析研究, 即相位角从0°到180°之间膜表面的参数分布规律。
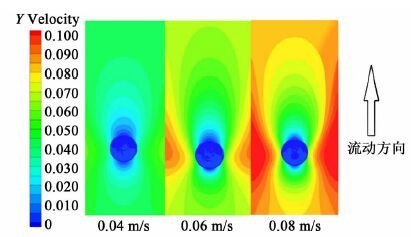
3.1 速度分布料液流速是影响流体对流传热的主要因素之一, 膜表面的对流传热速率受到膜表面流速的影响, 因此纤维表面的料液流速对整个传热过程十分重要。图 4显示了不同料液流速下纤维管横截面的速度云图。
|
| 图 4 纤维表面流动速度分布云图 Figure 4 Velocity contours on fiber surface |
| |
图 4中可以看出, 在纤维的前后两侧存在明显的流动边界层, 料液流速较低, 而在纤维左右两侧膜表面流速与料液主体流速之间的差值较小;当料液主体流速增大时, 纤维前后两侧的低流速边界层区域明显收缩, 纤维左右两侧与料液主体流速差值较小的区域扩大。
为了从数据上对纤维表面不同位置处速度分布及料液主体流速对膜表面流速的影响, 在相位角0°到180°之间每隔18°选取1个参数点, 对选取点的速度值进行分析, 按照相位角大小进行排列, 各点上速度分布曲线如图 5所示。

|
| 图 5 不同料液流速下纤维表面局部速度分布 Figure 5 Local velocity distribution on fiber surface at different bulk velocities |
| |
图 5中可以看出, 在研究的3种料液流速下纤维表面流速从相位角0°到180°的分布呈现先增大后减小的规律, 在相位角72°位置处纤维膜表面的速度最大, 而在纤维膜相位角为0°和180°处纤维膜表面的速度值非常小, 当主体流速为0.08 m/s时这两处的流速也小于0.005 m/s。这是因为在料液流经圆柱形的纤维膜丝时, 在圆柱的前后(相位角为0°和180°处)均存在较厚的流动边界层(如图 4所示), 而在相位角为72°位置处料液流动对纤维膜表面形成直接冲击, 边界层较薄, 流速较大。当料液流动速度增大时, 纤维表面速度也相继增大, 但是在靠近相位角为0°和180°位置处膜表面速度增加不明显, 而在其他位置处膜表面速度的增加非常显著。这说明增加料液流速可以显著提高纤维膜表面的料液流速, 有利于促进膜表面的热量和质量传递。另一方面, 虽然增大流速可以减小该边界层区域, 但是在纤维前后侧流动边界层仍然十分明显, 流动状态并未得到改善, 因此强化纤维膜表面的流动可以考虑如何强化纤维膜前后侧的流动状态来显著改善纤维膜表面整体速度分布, 比如对纤维膜丝施加合理的振动等。
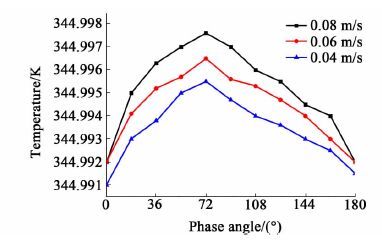
3.2 温度分布膜蒸馏过程是以温度差引起的饱和蒸汽压差为传质推动力, 因此膜表面的温度分布对传质过程至关重要;另一方面, 膜表面温度与料液主体之间的差值也说明了膜表面蒸发所需热量与对流传热量之间的平衡关系。与3.1节中速度分布选取的点相同, 对这些点上的温度分布规律进行分析, 分布曲线如图 6所示。
|
| 图 6 料液流速对环纤维表面温度的影响(料液温度345 K, 真空度0.06 MPa) Figure 6 Influence of bulk velocity on fiber surface (bulk temperature at 345 K, vacuum degree at 0.06 MPa) |
| |
分析图 6中不同料液主体流速下纤维膜表面温度分布规律可知, 温度分布规律与纤维膜表面的速度分布规律相似, 在相位角为72°处有最大值, 与料液主体温度345K相差很小, 而在相位角为0°和180°位置处膜表面温度与料液主体温度差较大。这是因为在料液流动速度较大的位置处料液湍流程度高, 对流传热系数大, 膜表面与料液主体之间的热量传递较快。膜表面的温度反映了对流传热热量与水蒸发相变带走热量之间的平衡关系, 蒸发速率越高, 带走的热量越大, 膜表面温度相应降低, 引起蒸发速率降低, 最终达到热量平衡。
从图 6中还可以看出, 膜表面的温度分布随着料液主体流速的增大而升高。由3.1的结果可知, 膜表面的速度与料液主体速度成正相关, 因此提高料液主体速度后膜表面的对流传热系数增大, 料液主体与膜表面之间的热量传递加快, 膜表面的温度升高, 流速变化越显著的位置处温度增大越明显, 例如相位角为72°位置附近处。
图 7显示了不同操作真空度对环纤维表面温度分布的影响规律。
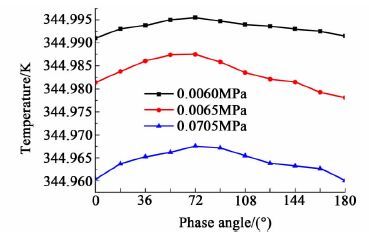
|
| 图 7 真空度对纤维表面温度的影响 Figure 7 Influence of vacuum degree on temperature of fiber surface |
| |
从图 7中可以看出, 随着真空度的增大纤维表面的温度显著降低。当提高操作真空度后, 纤维膜两侧的压力差增大, 即蒸发传质推动力增大, 膜表面液态水汽化蒸发速率增大, 所需的热量增加, 而纤维表面流动状态不变, 因此纤维表面温度降低。
3.3 蒸发速率分布为研究膜表面不同曲面区域的蒸发速率大小, 按照相位角大小将相位角0°到180°之间的纤维膜表面分为6个区域, 每个曲面区域对应的圆心角均为30°, 考察了蒸发速率在这些曲面上的平均值分布规律和料液流速以及真空度对蒸发速率的影响。
图 8显示了这些曲面上的平均蒸发速率分布规律。
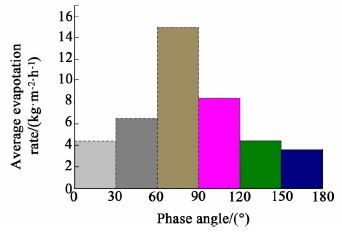
|
| 图 8 纤维膜表面蒸发速率分布规律(料液流速0.04 m/s, 真空度0.06 MPa) Figure 8 Evaporation rate distribution on hollow fiber surface (bulk velocity at 0.04 m/s, vacuum degree at 0.06 MPa) |
| |
由图 8中可以看出, 在相位角60°到90°之间膜表面上的平均蒸发速率最大, 而相位角0°到30°以及150°到180° 2个曲面上的平均蒸发速率较小。造成膜表面蒸发速率差的主要原因是膜表面的温度分布差异, 温度影响着水和水蒸气之间的气液平衡关系。从图 5和图 6的分析可知, 在相位角为60°到90°之间膜表面平均流速、温度均高于膜表面其他位置处, 热量传递速度和膜两侧蒸汽压差较大, 保证了蒸发所需的热量来源, 因此在纤维膜表面的该位置处蒸发传质速率大。从纤维表面蒸发速率的总体分布看来, 热料液在壳程中流动的错流式中空纤维减压膜蒸馏过程中膜通量的主要贡献来自于蒸发速率较大的位置, 即相位角30°到120°之间。
本研究还考察了料液主体流速和冷侧真空度对蒸发速率的影响, 选取相位角为60°到90°之间的纤维膜表面进行研究, 因为在该曲面上蒸发速率较大, 操作条件对其是否有影响可以显著的反映出来。固定料液主体流速为0.06 m/s, 对比了在真空度0.060、0.065和0.070 MPa下的蒸发速率;研究流速对蒸发速率影响时, 真空度固定为0.06 MPa, 分别考察了料液流速为0.04、0.06和0.08 m/s下膜表面的蒸发速率。模拟结果如图 9所示。

|
| 图 9 真空度和料液流速对蒸发速率的影响 Figure 9 Influence of vacuum degree and bulk velocity on evaporation rate |
| |
从图 9中可以看出, 增大真空度和增大料液主体流速均能提高纤维膜表面的蒸发速率, 而真空度的增大对蒸发速率的增加更加显著;随着料液流速的加大, 蒸发速率虽然仍然增大, 但是其增加量变小。从公式(10) 可以看出, 蒸发的传质推动力和真空度成线性正相关, 因此膜蒸馏过程中蒸发速率与真空度几乎成线性关系;随着料液流速的增大, 膜表面的传热速率增大, 膜表面的温度升高, 在其他条件不变时温度对蒸发速率的影响变弱, 即对流传热对蒸发速率的影响不再显著, 单纯增加流速对提高蒸发速率的效果不明显。
从以上研究可知, 强化膜通量除了改变操作条件外, 还可以考虑如何增大膜表面的高效蒸发区, 即减小膜表面边界层较厚的区域, 强化纤维膜相位角0°和180°位置处的流动状态, 增大这些区域的对流传热系数, 达到强化膜通量的目的。
3.4 传热系数分布对纤维膜表面的对流传热系数分析与3.3中的处理方式相同, 即将相位角从0°到180°之间的纤维表面分为6个区域, 考察这些曲面上的平均传热系数的分布情况。对流传热系数根据公式(14) 计算求得。图 10显示在料液流速0.04 m/s、真空度为0.06 MPa下纤维表面的对流传热系数分布规律。
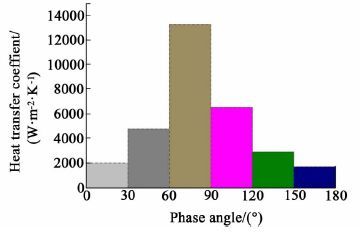
|
| 图 10 纤维膜表面不同位置处对流传热系数分布(料液流速0.04 m/s, 真空度0.06 MPa, 料液温度345 K) Figure 10 Heat transfer coefficient distribution of hollow fiber surface (bulk velocity at 0.04 m/s, bulk temperature at 345 K and vacuum degree at 0.06 MPa) |
| |
从图 10中可以看出, 在纤维膜表面的不同位置处对流传热系数各不相同, 在相位角为30°到120°之间的膜表面对流传热系数显著大于其他曲面, 在相位角60°到90°之间的传热系数尤其显著, 远高于其他位置处。这是因为在该位置处纤维膜表面的温度与料液主体温度之间的温差较小, 另一方面从3.3中蒸发速率分布的分析可知, 在这些位置处的蒸发量也高于其他曲面, 由公式(14) 计算所得的对流传热系数较大。在膜表面相位角为0°和180°附近对流传热系数较小, 这与该位置处流动速度较小、湍流程度低和边界层较厚的流动特点相吻合, 因为边界层的存在严重阻碍了热量从主体料液中向膜表面传递。
本研究中也考察了操作条件对传热系数的影响, 与3.3中对蒸发速率的分析相同, 选取相位角在60°到90°之间的纤维表面进行对比分析, 研究真空度和料液流速对该曲面上传热系数的平均值的影响。模拟计算结果如图 11所示。

|
| 图 11 真空度和料液流速对传热系数的影响 Figure 11 Influence of vacuum degree and bulk velocity on heat transfer coefficient |
| |
从图 11中可知, 传热系数随着真空度的提高迅速降低, 而料液流速的增大有利于增大对流传热系数。综合图 7和图 9可知, 真空度的提高增加了纤维膜的传质通量, 蒸发过程所需的热量也相应增加, 膜表面的温度与料液主体温度之间的温度差变大;根据传热系数计算公式(14) , 虽然膜通量增大有利于传热系数的提高, 但是温差对传热系数的影响更加敏感, 综合结果是真空度增大后膜表面的传热系数显著降低。料液流速增大时, 纤维膜表面的温度升高, 与料液主体之间的温差进一步缩小, 同时膜表面的蒸发速率也增大, 膜通量增加, 因此提高料液流速后对流传热系数也相应增大。
4 结论错流式中空纤维减压膜蒸馏过程的模拟研究表明, 中空纤维膜表面的热质传递参数随着位置的不同而发生变化, 在相位角为60°到90°之间料液流速、温度、蒸发速率以及对流传热系数均大于其它膜表面, 膜通量的主要贡献来自于相位角30°到120°之间的纤维表面;增大料液流速纤维表面的速度、温度、蒸发速率和传热系数均不同程度的增大, 有利于膜通量的提高, 强化膜蒸馏过程;纤维表面的蒸发速率与真空度成线性正相关, 而传热系数随着真空度的提高迅速降低。本研究结果有利于从微观层面上增加对减压膜蒸馏过程的理解, 膜蒸馏过程的强化可以考虑强化纤维前后侧边界层较厚区域的流动状态, 增大高效蒸发区域面积。
| [1] | Abdullah AND, Nidal H. Membrane distillation:A comprehensive review[J]. Desalination , 2012, 287 : 2–18. DOI: 10.1016/j.desal.2011.08.027 |
| [2] | 陈迅, 蒋绍阶, 岳崇峰, 等. 减压膜蒸馏浓缩脱硫液试验研究[J]. 中国给水排水 , 2014 , 30 (11) : 139–143. Chen Xun, Jiang Shaojie, Yue Chongfeng, et al. Study on concentration of desulfurization solution by vacuum membrane distillation[J]. China Water & Wastewater , 2014, 30(11) : 139–143. |
| [3] | 刘学晶, 李保安. 减压膜蒸馏热量回收过程研究[J]. 化学工业与工程 , 2014 , 31 : 38–42. Liu Xuejing, Li Baoan. Heat recovery in vacuum membrane distillation[J]. Chemical Industry and Engineering , 2014, 31 : 38–42. |
| [4] | 吕双江. 减压多效膜蒸馏过程研究[D]. 天津:天津工业大学, 2013 Lv Shuangjiang. Study of vacuum multi-membrane distillation process[D]. Tianjin:Tianjin University of Technology, 2013(in Chinese) |
| [5] | 朱春英, 高振, 高习群, 等. 真空膜蒸馏过程膜参数模拟计算[J]. 化学工程 , 2006 , 34 (9) : 35–38. Zhu Chunying, Gao Zhen, Gao Xiqun, et al. Simulation and calculation of membrane parameters in vacuum membrane distillation[J]. Chemical Engineering , 2006, 34(9) : 35–38. |
| [6] | 刘典. 陶瓷膜疏水改性与真空膜蒸馏过程模拟研究[D].上海:华东理工大学, 2012 Liu Dian. Modification of ceramic membrane and its use in VMD[D]. Shanghai:East China University of Science and Technology, 2012(in Chinese) |
| [7] | Zhang L, Xiang J, Cheng P, et al. Three-Dimensional numerical simulation of aqueous NaCl solution in vacuum membrane distillation process[J]. Chemical Engineering and Processing:Process Intensification , 2015, 87 : 9–15. DOI: 10.1016/j.cep.2014.11.002 |
 2016, Vol. 33
2016, Vol. 33





