石油化工过程中排出的含油废水对水资源、生态环境都会造成很大的污染。随着人们环保意识的日益增强加强,对含油废水的处理逐渐成为石化产业及环境工程领域的研究热点。含油废水处理过程的核心步骤为油水两相的分离,目前主要方法有机械法、化学法、物理化学法和生物法等,对各方法的工艺设备进行优化设计能够提高油水分离效率[1-4]。重力式油水分离器是机械法中比较初级的设备,其分离效果对后续设备的工作状况影响显著[5]。重力式油水分离器的工作效率相对低,对分散相的粒径要求较高,但它具有结构简单、运行稳定等诸多优点,所以应用较为广泛。由Strokes定理可知,分散相的粒径越小,分离效果越不理想[6],所以在设备内安装聚结构件以增大分散相粒径是目前比较普遍的改进方法[7]。
重力式分离器内油水混合流体在进入聚结构件时越接近水平柱塞流,油水分离效果越高,设备的体积利用率越高。重力式油水分离器内轴向流动状态是考察分离流场的标准之一[8],轴向流速的Mf越小说明越接近水平柱塞流,混合流体在平行板聚结器板间的流动越稳定,油滴能够更快速地上浮到聚结板下底面进行聚结。入口构件型式在很大程度上决定了轴向流动状态,所以选择合适的入口构件并进行优化设计对于提升油水分离效率非常关键[9-10]。其中,圆孔分散式入口构件能够以相对较短的距离实现水平柱塞流,相同位置的Mf相对其他入口构件型式更小。
目前研究流体力学方法主要有实验流体力学(EFD)和计算流体力学(CFD)法[11]。CFD数值模拟法的巨大优势在于能够更清楚地理解体系内流动状态,并提供大量定性或定量的关于速度场和湍流场的信息。而EFD法要想获得这些信息需要使用一些昂贵而复杂的大型仪器,比如粒子成像测速仪(PIV)等。此外,CFD法还非常适用于结构复杂、设计变量较多的实验模型,所以将CFD法应用于重力式油水分离器,尤其是入口构件的研究中,可以避免实际实验中复杂的设计和优化改进过程,从而更有效地获取体系内各种动力学现象和规律,用于指导实际操作过程。Abdulkadir和Hernandez-Perez[12]成功地运用CFD法得到混合物入口流速、分散相粒径与分离效果之间的关系;原广庆等[13]依据模拟所得速度矢量图分析了入口构件、整流构件对重力分离设备流动特性的影响;吕玉玲等[14]也通过CFD法对几种板式聚结构件的流动特性进行了研究。
本研究将一种圆孔分散式入口构件加以改进应用于重力式油水分离器,主要目的就是对该形式的入口构件的进行优化设计,找到待考察的结构参数的最优化组合,使重力式油水分离器内流体在进入聚结构件之前尽可能实现水平柱塞流,即轴向流速Mf达到最小。考虑到各参数之间可能存在交互作用,本研究在单因素CFD分析的基础上,继续使用响应面分析法[16]对各参数进行优化设计。
1 数值模型及评价标准 1.1 建模与网格划分圆孔分散式入口构件如图 1所示,在入口构件的半球面封头和圆柱侧面上均匀开孔,两组圆孔半径分别为r1、r2,分布方式固定,侧面孔口到半球面封头边缘的距离为l1;入口直径d2=0.16D=40 mm;保持封头和侧面上的圆孔数分别为n1=30、n2=60。3个待考察的无因次结构参数分别为:1) P1为入口构件上圆孔面积与分离器筒体横截面面积之比;2) P2为半球面封头与圆柱侧面上圆孔面积之比;3) P3为l1与分离器筒体横截面直径(D)之比。

|
| 图 1 圆孔分散式入口构件 Figure 1 Inlet component with round orifices |
| |
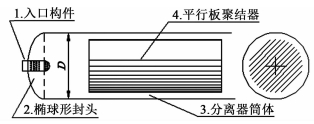
重力式油水分离器整体几何结构,包括入口构件、分离器筒体、聚结构件等,示意图见图 2。模拟过程中只考察入口构件在分离器筒体内产生的流动特性,筒体结构参数为:圆形横截面直径D=250 mm;轴向筒长为L=6D=1 500 mm(不包括2个椭球形封头);椭球封头的短半径为r3=0.25D=62.5 mm;两相出口的半径都为设为r4=15 mm。
|
| 图 2 重力式油水分离器几何结构 Figure 2 Geometry of the gravity oil/water separator |
| |
借助Gambit软件对模型划分网格,采用自适应性的非结构网格。前期模拟过程进行网格无关性研究,同时考虑计算结果准确性和计算时间合理性,最终选择采用约50万网格,不同结构参数组合的入口构件使网格数稍有差异。
1.2 体系与控制方程本研究的油水分离体系中,油相含量相对较少,在分离器内油水两相流的流动状态与单相流(水)基本一致,所以模拟采用水(ρ=1 000 kg/m3,μ=1.003×10-3 Pa·s)单相流代替两相流简化计算过程。流动过程涉及圆孔喷射流且局部流动达到强烈的湍流状态,所以计算过程选用Realizable k-ε湍流模型[17]。本研究中不涉及传热过程,采用雷诺平均(RANS)法处理后的控制方程如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0 $ | (1) |
| $ \begin{gathered} \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \hfill \\ \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {{{u'}_i}{{u'}_j}} } \right) + {S_i} \hfill \\ \end{gathered} $ | (2) |
式(2)中
| $ \overline {{{u'}_i}{{u'}_j}} = - {\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) + \frac{2}{3}\left( {\rho k + {\mu _t}\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right){\delta _{ij}} $ | (3) |
| $ {\mu _t} = \rho {C_{\text{\mu }}}\frac{{{k^2}}}{\varepsilon } $ | (4) |
式(3)和(4)中,ui为时均速度;δij是“Kronecker Delta”符号(当i=j时,δij=1;当i≠j时δij=0);k为湍动能;μt为湍动黏度。
Realizable k-ε模型中,湍动能k和耗散率ε的输运方程分别为:
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\text{t}}}}}{{{\sigma _{\text{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon $ | (5) |
| $ \begin{gathered} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}E\varepsilon - \\ \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\upsilon \varepsilon } }} \\ \end{gathered} $ | (6) |
式(5)和(6)中,σk=1.0、σε=1.2、C2=1.9[18]。
1.3 计算方法与边界设置所有CFD数值模拟计算通过Fluent 6.3软件实现,采用基于有限体积法的SIMPLE算法,动量、湍动能及湍动能耗散率的差分格式均采用first-order upwind格式,压力插分格式选择standard格式。
速度边界条件:velocity-inlet;uin=0.035 m/s。
设定设备中安装平行板聚结器,板层与水平方向倾角为45°,根据工程上的经验将聚结器板层之间的间距选定为l2=20 mm,聚结构件长l=2D=500 mm,假设油滴瞬间达到最大上浮速度vt,依据Strokes公式可得:
| $ {\upsilon _{\text{t}}} = \frac{{gd_{\text{p}}^2\Delta \rho }}{{18\mu }} $ | (7) |
式(7)中,dp为油滴直径;油水两相密度差Δρ=ρ水-ρ油=1 000-870=130 kg/m3;μ为连续相的黏度。
流场中流体的平均流速为:
| $ \bar u = {u_{{\text{in}}}}{\left( {\frac{D}{{{d^2}}}} \right)^2} $ | (8) |
设最小油滴恰好能在聚结板上附集则可得:
| $ \frac{{{L_{{\text{eff}}}}}}{{{d_3}/\cos 45^\circ }} = \frac{{0.7L}}{{{d_3}/cos45^\circ }} = \frac{{\bar u}}{{{u_{\text{t}}}}} $ | (9) |
式(9)中,Leff为沉降过程中板组的有效长度。
通过式(8~9)可求得在聚结板上附集油滴的最小粒径为32.0 μm,而工业中对板式聚结构件能实现附集聚结油滴的粒径要求通常为30~50 μm,所以本研究中预设的平行板聚结器工作性能良好。
油水两相出口的边界条件:outflow。油相出口和水相出口的体积流量分数分别为5%和95%。所有壁面条件:wall。
1.4 轴向速度相对不均匀度的计算方法分离器筒体圆形横截面上轴向速度相对不均匀度(Mf)定义式为[19]:
| $ {M_{\text{f}}} = \sqrt {\frac{1}{n}\sum\limits_{j = 1}^n {{{\left[ {\frac{{{u_i} - \bar u}}{{\bar u}}} \right]}^2}} } = \frac{1}{{\bar u}}\sqrt {\frac{1}{n}\sum\limits_{j = 1}^n {{{\left( {{u_i} - \bar u} \right)}^2}} } $ | (10) |
式(10)中,ui为截面上任意点轴向速度;为所有点的平均值。
2 计算结果与分析 2.1 前期模拟前期模拟过程主要是定性考察采用圆孔分散式入口构件在入口段产生的流场流型,发现主要有两种,如图 3所示。

|
| 图 3 入口段两种不同的流型 Figure 3 Two different flow patterns in the entrance part |
| |
对于流型Ⅰ,大部分流体主要从半球形封头进入分离器内,在流动一段距离后在顶部和底部出现流体的反转,此时Mf较大,这非常不利于下游的聚结过程。而对于流型Ⅱ,大部分流体主要从侧面圆孔进入分离器内,从图 3中可以清楚地看出该流型状态下,虽然在入口附件产生了一定的涡流,但流体会以较短的距离实现水平柱塞流,且无明显流体反转现象,这非常利于下游的聚结过程,所以对入口构件进行优化设计时要尽可能使流体处于流型Ⅱ的状态下。对模拟结果的进一步分析发现当处于流型Ⅱ状态时,在距离入口构件100~150 mm的范围内流体逐渐接近水平柱塞流,所以假设在距离入口构件150 mm处开始安装聚结构件,并将此处圆形横截面上轴向速度的Mf作为入口构件优化设计的评价标准。
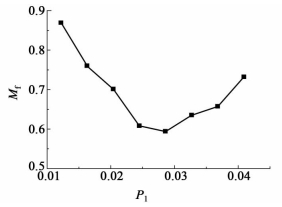
2.2 单因素CFD分析 2.2.1 入口构件上圆孔面积与分离器横截面面积之比P1对Mf的影响P2和P3为固定值,分别等于0.1和0.048,P1取0.012、0.016、0.021、0.025、0.029、0.033、0.037和0.041进行模拟计算,分别得到相应的Mf值,结果见图 4。
|
| 图 4 Mf随P1变化图 Figure 4 Variation of Mf with increasing P1 |
| |
从图 4可以看出Mf随P1的增大呈现出先减小后增大的趋势。P1取较小值时,入口构件上开孔面积较小,而进入分离器的流体的流量不变,所以流速较大,湍动强度也较大,对下游的干扰作用增强,相应的Mf偏大;当P1取较大值时,在惯性力的作用下更多的流体从封头孔口流出,即增大了封头的出流量,趋向于形成流型Ⅱ,所以Mf有所增大。当P1为0.029左右时,即P1 min=0.1时,Mf达到最小。
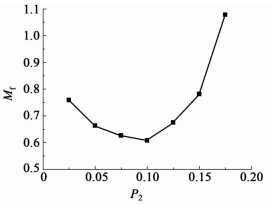
2.2.2 半球面封头与圆柱侧面上圆孔面积比P2对Mf的影响固定P1为0.029,P3为0.048。P2分别取0.025、0.05、0.075、0.1、0.125、0.15、0.175进行分析,模拟结果见图 5。
|
| 图 5 Mf随P2变化图 Figure 5 Variation of Mf with increasing P2 |
| |
P2为0.025时,几乎所有流体从侧面流出,侧面出流形成的涡流强度影响范围较大,导致15 mm处仍然受其影响显著,相应的Mf较大,所以在随P2的增大,封头孔口的分流作用在一定程度上会使这种影响逐渐削弱,相应的Mf有所减小。但当P2增大到0.1左右(P2 min=0.1)时,Mf达到最小,此时封头出流的强烈冲击对下游流场产生的扰动开始占主导,相应的Mf开始增大,并使流场的由流型Ⅱ向流型Ⅰ过渡转变。
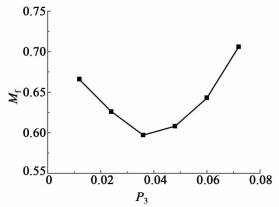
2.2.3 侧面孔口到半球面封头边缘的距离与分离器横截面直径之比P3对Mf的影响固定P1为0.029,P2为0.1。P3分别取0.012、0.024、0.036、0.048、0.060和0.072进行数值计算,发现P3 min为0.036左右时,Mf达到最小,如图 6所示。
|
| 图 6 Mf随P3变化图 Figure 6 Variation of Mf with increasing P3 |
| |
P3决定侧面和封头上的圆孔出流之间相互作用的强度,P3较小时两组圆孔之间的相互作用加强,使入口附近湍动强度增大,对下游流场扰动增大,Mf也随之增大。而P3较大时,两组孔之间的距离增大,圆孔出流分散不均匀,同样使入口附近和下游流场的扰动增强。
2.3 响应面CFD分析 2.3.1 因素与水平根据Box-Benhnken的中心组合实验设计原理,在上述单因素CFD模拟结果(P1 min=0.029;P2 min=0.1;P3 min=0.036)的基础上,采用响应面分析法寻找研究因素的最优化组合以及可能存在的相互作用。以P1、P2和P3为研究因素,分别选取3个水平,见表 1。
| 因素 | 水平 | ||
| -1 | 0 | 1 | |
| P1 | 0.025 | 0.029 | 0.033 |
| P2 | 0.075 | 0.100 | 0.125 |
| P3 | 0.024 | 0.036 | 0.048 |
对P1、P2、P3做如下变换:
| $ X = {F_1}\left( {{P_1}} \right) = \frac{{\left( {{P_1} - 0.0287} \right)}}{{0.0041}} $ | (11) |
| $ Y = {F_2}\left( {{P_2}} \right) = \frac{{\left( {{P_2} - 0.1000} \right)}}{{0.0250}} $ | (12) |
| $ Z = {F_3}\left( {{P_3}} \right) = \frac{{\left( {{P_3} - 0.0360} \right)}}{{0.0120}} $ | (13) |
以X、Y、Z为自变量,以距离入口构件150 mm处圆形横截面上的轴向速度的Mf为响应值,建立3因素3水平的设计方案,方案及模拟结果见表 2。编号1~12是析因数值模拟计算结果;编号13~16是中心数值模拟计算结果,通过增加网格的尺寸重复4次,以满足对失拟项显著程度的考察。
| 编号 | X | Y | Z | Mf |
| 1 | -1 | -1 | 0 | 0.667 |
| 2 | -1 | 0 | -1 | 0.662 |
| 3 | -1 | 0 | 1 | 0.662 |
| 4 | -1 | 1 | 0 | 0.646 |
| 5 | 0 | -1 | -1 | 0.665 |
| 6 | 0 | -1 | 1 | 0.648 |
| 7 | 0 | 1 | -1 | 0.621 |
| 8 | 0 | 1 | 1 | 0.697 |
| 9 | 1 | -1 | 0 | 0.621 |
| 10 | 1 | 0 | -1 | 0.611 |
| 11 | 1 | 0 | 1 | 0.659 |
| 12 | 1 | 1 | 0 | 0.675 |
| 13 | 0 | 0 | 0 | 0.590 |
| 14 | 0 | 0 | 0 | 0.584 |
| 15 | 0 | 0 | 0 | 0.586 |
| 16 | 0 | 0 | 0 | 0.570 |
利用Design-Expert软件对X、Y、Z进行二次多项式拟合,结果如下:
| $ \begin{gathered} {M_{\text{f}}} = G\left( {X,Y,Z} \right) = 0.5823 - 0.008841X + \\ 0.004900Y + 0.001332Z + 0.001874XY + \\ 0.001204XZ + 0.002345YZ + 0.003025{X^2} + \\ 0.003978{Y^2} + 0.003589{Z^2} \\ \end{gathered} $ | (14) |
对拟合模型进行方差分析得表 3。
| 方差来源 | 自由度 | 平方和 | 均方 | F值 | P>F | 显著性 |
| 回归 | 9 | 0.022 | 2.396×10-3 | 28.43 | 0.0003 | 显著 |
| X | 1 | 6.253×10-4 | 6.253×10-4 | 7.42 | 0.0345 | |
| Y | 1 | 1.921×10-4 | 1.921×10-4 | 2.28 | 0.1819 | |
| Z | 1 | 1.420×10-3 | 1.420×10-3 | 16.85 | 0.0063 | |
| XY | 1 | 1.405×10-3 | 1.405×10-3 | 16.67 | 0.0065 | |
| XZ | 1 | 5.796×10-4 | 5.796×10-4 | 6.88 | 0.0395 | |
| YZ | 1 | 2.200×10-3 | 2.200×10-3 | 26.10 | 0.0022 | |
| X2 | 1 | 3.661×10-3 | 3.661×10-3 | 43.44 | 0.0006 | |
| Y2 | 1 | 6.329×10-3 | 6.329×10-3 | 75.09 | 0.0001 | |
| Z2 | 1 | 5.149×10-3 | 5.149×10-3 | 61.10 | 0.0002 | |
| 残差 | 6 | 5.057×10-4 | 8.428×10-5 | |||
| 失拟项 | 3 | 2.741×10-4 | 9.138×10-5 | 1.18 | 0.4464 | 不显著 |
| 纯误差 | 3 | 2.315×10-4 | 7.717×10-5 | |||
| 总和 | 15 | 0.022 | ||||
| 注:(1)f0.01(9, 5)=10.20,f0.05(3, 2)=19.20,f0.10(3, 2)=9.16;(2)P表示概率。 | ||||||
由表 3可知拟合方程的方差齐性检验F=28.43>f0.01(9, 5),所以该方程是显著的;此外,失拟项不显著说明方程对数值模拟结果的拟合情况好,可用该方程代替数值模拟分析优化结果。
图 7~图 9是X、Y、Z对Mf影响的响应面图和等值线图,从图中可以直观看出P1、P2、P33个参数对Mf的影响之间存在交互作用,在式(14)中体现为二次交叉项的系数不为0。随P1、P2、P3的增大Mf都呈现出先减小后增大的趋势,存在最小值,与单因素CFD分析的趋势基本一致。通过比较3组图曲线的弯曲程度也可看出,P1、P2、P3对Mf值影响的显著性相差不大。

|
| 图 7 Mf=G(X, Y)的响应面图和等值线图 Figure 7 Responsive surface and contour of Mf=G(X, Y) |
| |

|
| 图 8 Mf=G(X, Z)的响应面图和等值线图 Figure 8 Responsive surface and contour of Mf=G(X, Z) |
| |

|
| 图 9 Mf=G(Y, Z)的响应面图和等值线图 Figure 9 Responsive surface and contour of Mf=G(Y, Z) |
| |
为了确定每个参数的最优值,对回归方程求一阶偏导数并令其等于0,整理得:
| $ \left\{ \begin{gathered} 60.51X + 18.74Y + 12.04Z - 8.841 = 0 \hfill \\ 18.74X + 79.55Y + 23.45Z + 4.900 = 0 \hfill \\ 12.04X + 23.45Y + 71.75Z + 13.21 = 0 \hfill \\ \end{gathered} \right. $ | (15) |
求解可得出X、Y、Z的最适宜值分别为X=0.2018,Y=-0.0492,Z=-0.2034,即P1、P2、P3三因素的取值分别为0.029、0.1和0.036。将X、Y、Z回带至方程(14)中得出,此条件下Mf的理论最小值为0.58。
3 结论将圆孔分散式入口构件安装于重力式油水分离器中,入口段流型主要有两种:流型Ⅱ相对于流型Ⅰ实现水平柱塞流所需的距离较短,在距离入口构件处100~150 mm处基本实现同向流动,对入口构件的优化设计时要保证流体处于流型Ⅱ状态下。
以距离入口构件150 mm处圆形横截面的轴向速度的Mf为评价标准,通过单因素CFD模拟分析发现Mf随3个参数P1、P2、P3的增大都呈现出先减小后增大的趋势。
根据Box-Benhnken原理设计3因素3水平方案,通过响应面分析得出:P1、P2、P3的取值对Mf影响的显著性相差不大且相互之间存在交互作用;当P1、P2、P3的取值分别为为0.029、0.1和0.036时,Mf有理论最小值0.58。
| [1] | 张翼, 于婷, 毕永慧, 等. 含油废水处理方法研究进展[J]. 张翼, 于婷, 毕永慧, 等. 2008. 含油废水处理方法研究进展[J]. 化工进展 , 2008 , 27 (8) : 1 155–1 161. Zhang Yi, Yu Ting, Bi Yonghui, et al. Progress of oily wastewater treatment[J]. Chemical Industry and Engineering Progress , 2008, 27(8) : 1 155–1 161. |
| [2] | 殷永泉, 邓兴彦, 刘瑞辉, 等. 石油化工废水处理技术研究进展[J]. 殷永泉, 邓兴彦, 刘瑞辉, 等. 2006. 石油化工废水处理技术研究进展[J]. 环境污染与防治 , 2006 , 28 (5) : 356–360. Yin Yongquan, Deng Xingyan, Liu Ruihui, et al. Technology for treatment of petrochemical[J]. Environment Pollution & Contol , 2006, 28(5) : 356–360. |
| [3] | 谢磊, 胡勇友, 钟海涛. 含油废水处理技术进展[J]. 谢磊, 胡勇友, 钟海涛. 2003. 含油废水处理技术进展[J]. 工业水处理 , 2003 , 23 (7) : 4–7. Xie Lei, Hu Yongyou, Zhong Haitao. Oil-Bearing wastewater treatment processes and progress[J]. Industry Water Treatment , 2003, 23(7) : 4–7. |
| [4] | 李国珍, 肖华, 董守平. 油水分离技术及其进展[J]. 李国珍, 肖华, 董守平. 2001. 油水分离技术及其进展[J]. 油气田地面工程 , 2001 , 20 (2) : 7–9. Li Guozhen, Xiao Hua, Dong Shouping. Oil-Water separation technology and progress[J]. Oil-Gas Field Surface Engineering , 2001, 20(2) : 7–9. |
| [5] | Ali P L, William Y S, Wayne D M. Design and CFD studies of multiphase separators:A review[J]. The Canadian Journal of Chemical Engineering , 2011, 9 999 : 1–14. |
| [6] | Maurice S, Ken A. Emulsions and oil treating[M]. Burlington: Gulf Professional Publishing, 2009 . |
| [7] | 陈文征, 张贵才, 尹海峰. 波纹板聚结油水分离技术研究进展[J]. 陈文征, 张贵才, 尹海峰. 2007. 波纹板聚结油水分离技术研究进展[J]. 石油矿场机械 , 2007 , 36 (5) : 27–29. Chen Wenzheng, Zhang Guicai, Yin Haifeng. The development of the corrugated plates coalescing oil-water separation technology[J]. Oil Field Equipment , 2007, 36(5) : 27–29. |
| [8] | Wilkinson D, Waldie B, Mohamad N M I, et al. Baffle plate configuration to enhance separation in horizontal primary separators[J]. Chemical Engineering Journal , 2000, 77 : 221–226. DOI: 10.1016/S1385-8947(99)00170-9 |
| [9] | 陆耀军, 潘玉琦, 薛敦松. 重力式油水分离设备入口构件的模拟实验优选[J]. 陆耀军, 潘玉琦, 薛敦松. 1995. 重力式油水分离设备入口构件的模拟实验优选[J]. 石油学报 , 1995 , 16 (3) : 111–115. Lu Yaojun, Pan Yuqi, Xue Dunsong. The simulation tests and optimized study on input components of gravity oil-water separators[J]. Acta Petrolei Sinica , 1995, 16(3) : 111–115. |
| [10] | 陆耀军, 薛敦松. 重力式油水分离设备结构优化模型[J]. 陆耀军, 薛敦松. 1999. 重力式油水分离设备结构优化模型[J]. 化工学报 , 1999 , 50 (2) : 273–279. Lu Yaojun, Xue Dunsong. Geometry optimization of gravity oil-water separation[J]. Journal of Chemical Industry and Engineering , 1999, 50(2) : 273–279. |
| [11] | Blazek J. Computational fluid dynamics: Principles and applications[M]. Oxford: Elsevier Ltd, 2005 . |
| [12] | Abdulkadir M, Hernandez-Perez V. The effect of mixture velocity and droplet diameter on oil-water separator using computational fluid dynamics[J]. World Academy of Science, Engineering and Technology , 2010, 61 : 35–43. |
| [13] | 原广庆, 张吕鸿, 张海涛, 等. 重力式油水分离器内部构件对流动特性的影响[J]. 原广庆, 张吕鸿, 张海涛, 等. 2008. 重力式油水分离器内部构件对流动特性的影响[J]. 石油化工设备 , 2008 , 37 (1) : 12–15. Yuan Guangqing, Zhang Lvhong, Zhang Haitao, et al. Study on field in gravity oil-water separators with regulating components[J]. Petro-Chemical Equipment , 2008, 37(1) : 12–15. |
| [14] | 吕玉玲, 何利民, 王国栋, 等. 含不同构件的重力式分离器内流场数值模拟[J]. 吕玉玲, 何利民, 王国栋, 等. 2008. 含不同构件的重力式分离器内流场数值模拟[J]. 石油机械 , 2008 , 36 (2) : 12–16. Lv Yuling, He Limin, Wang Guodong, et al. Simulation of flow field in gravitational oil-water separator with different components[J]. China Petroleum Machinery, , 2008, 36(2) : 12–16. |
| [15] | Nelson S R. Inlet distributor for liquid-liquid separator: US, 4479875 [P]. 1984-10-30 |
| [16] | 王永菲, 王成国. 响应面法的理论与应用[J]. 王永菲, 王成国. 2005. 响应面法的理论与应用[J]. 中央民族大学学报 , 2005 , 14 (3) : 236–240. Wang Yongfei, Wang Chengguo. The application of response surface methodology[J]. Journal of the CUN , 2005, 14(3) : 236–240. |
| [17] | ANSYS Inc. ANSYS FLUENT 12.0. Theory guid[M]. ANSYS Inc: 2009 |
| [18] | 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004 |
| [19] | 侯先瑞.重力式油水分离器性能的数值模拟[D].辽宁大连:大连海事大学, 2011 |
 2016, Vol. 33
2016, Vol. 33





