2. 天津市膜科学与海水淡化技术重点实验室, 天津 300072
2. Tianjin Key Laboratory of Membrane Science and Desalination Technology, Tianjin University, Tianjin 300072, China
近年来反渗透海水淡化技术迅猛发展,产水能耗已从20世纪80年代的8 kW·h·m-3降至现在的2.2 kW·h·m-3左右[1-2],能耗的降低很大程度上有赖于能量回收装置的全面利用。作为能量回收装置的典型代表,正位移式能量回收装置采用 “压力能→压力能”一步转化过程直接将高压盐水的压力能传递给低压海水,能量回收效率高达90%~95%,成为国内外研究和推广的重点[3-5]。
水力自驱旋转式能量回收装置(HRERD)遵循正位移式压力交换原理,利用参与压力交换的高、低压流体对装置转子的水力冲击作用,实现转子的旋转驱动及压力交换过程的连续进行,具有装置结构紧凑、操控简便、流体连续性好等优点。国外对该类型产品的研究开发较早,包括美国ERI公司的PX[6-8]和Isobarix公司的XPR[9-10]等,其中PX装置已在全球海水淡化工程中实现了商业推广[11];国内对该类型产品的研究起步较晚,目前还只是处于技术开发和样机试制阶段[12]。杨勇君等[13]利用流体力学软件FLUENT建立了RERD 装置三维非稳态滑移网格模型,研究分析了转速对装置盐度场分布的影响规律,模拟发现装置转速越大,增压出口的含盐量就越小。
研究HRERD的转子转速是水力自驱技术走向成熟必不可少的一个环节,转速的大小会影响装置转子通道内混合段液体的“外溢”程度,混合段液体“外溢”程度越大,装置增压出口的含盐量就越大,这会导致反渗透海水淡化系统进口管路含盐量增加,导致海水淡化系统的产水成本上升[14]。因此,获取HRERD的转子转速对于改善装置的性能至关重要。实验法和模拟法均可获取HRERD的转速,但只能直接获取一定条件下零散的速度点值或者速度场[15]。本研究运用动量定理分析了转子受流体水力冲击而产生的动力矩与转子转速的关系式;以微元法为基础,运用牛顿黏性定律分析了转子周面和端面因流体黏性阻力而产生的阻力矩与转子转速的关系式;利用转子稳定时所受动力矩与阻力矩间的平衡关系,推导得到装置转速与系统流量间的理论公式,该公式可用来计算稳定运行阶段时HRERD的转速,对于HRERD的结构优化设计、操作条件的规范具有一定的指导意义。
1 水力自驱旋转式能量回收装置工作原理图 1是水力自驱旋转式能量回收装置的工作原理示意图。图 1中的上端盘、转子、下端盘一起组成水力自驱旋转式能量回收装置的核心部件转芯。上下端盘的结构相同,对称的两区结构将端盘分成高压区、密封区以及低压区,在高压区和低压区的集液槽中均存在螺旋导流结构。

|
| 图 1 水力自驱旋转式能量回收装置的工作原理示意图 Figure 1 Working principle diagram of HRERD |
| |
工作时高压盐水通过高压盐水入口进入与其贯通的5个流体通道并将通道中的低压海水迅速增压并排出,此为增压过程;低压海水通过低压海水入口进入与其贯通的5个流体通道并将通道中的泄压盐水迅速排出,此为泄压过程。在增压和泄压过程中会有部分高压盐水和低压海水在螺旋导流结构的引流下形成对转子的冲击力,从而驱动转子转动。随着转子的转动,所有流体通道依次循环经过高压区-密封区-低压区-密封区-高压区,装置因此能连续高效的回收高压盐水压力能。
2 转子所受力矩分析 2.1 转子动力矩分析水力自驱旋转式能量回收装置端盘的高压盐水入口和低压海水入口形状相同,实际工作过程中这两个进口的流量保持相等,且这两股进口流体的流量值可被视为装置的处理量。即:
| $Q={{Q}_{bi}}={{Q}_{si}}$ | (1) |
为方便讨论,将处于任一工作位的转芯展开成二维平面,如图 2所示。图 2中箭头R方向为转子转动方向(顺时针方向),端盘进出口处箭头方向为所对应流体的流动方向。转子周向均布12个流体通道,将其依次编号为1#~12#通道。其中高压区覆盖转子1#~5# 5个流体通道,密封区覆盖转子6#、12# 2个流体通道,低压区覆盖转子7#~11# 5个流体通道。高压盐水和低压海水在转芯内的流通路线对称,故本研究以高压盐水对转子的冲击过程为例展开转子动力矩的计算过程。

|
| 图 2 转芯平面示意图 Figure 2 Schematic plan of rotor core |
| |
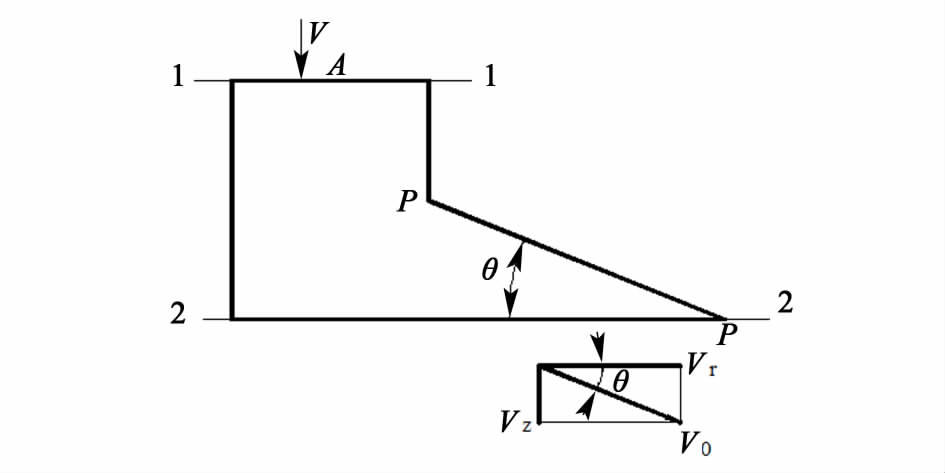
工作时高压盐水从高压盐水入口进入端盘,部分流体直接进入图 2所示的1#和2#流体通道;剩余流体经螺旋导流结构引流后顺着螺旋导流结构射出并流入3#~5#通道(由于螺旋导流结构与转子之间的端面间隙泄露量较小,故可将其忽略)。流体进入1#和2#流体通道时其速度方向与转子转动方向互相垂直,故进入这2个通道的流体将不形成对转子的有效冲击。本研究将被螺旋导流结构引流的这部分流体称为驱动流体,定义有效冲击系数k为驱动流体与入口流体流量之比。则驱动流体平均轴向速度(见图 3):
| ${{V}_{z}}=\frac{kQ}{3{{A}^{*}}}$ | (2) |
|
| 图 3 冲击角度示意图 Figure 3 Schematic diagram of impactingangle |
| |
由于螺旋导流结构末端的坡度比较平缓,故此处可假设3#~5#通道所对应的冲击角度相同。则驱动流体水平切向速度
| ${{V}_{r}}=\frac{{{V}_{z}}}{tan\theta }$ | (3) |
图 3中1-1截面为端盘的高压盐水入口截面,2-2截面为端盘与转子的分界面。
流体对转子的驱动过程可用动量定律表示为
| $F=\rho kQ\left( {{V}_{r}}-\omega r \right)\text{ }$ | (4) |
冲击转子后的流体与转子同步转动,故其残余角速度与转子的角速度相同。由转子的角速度与转速的关系可算出
| $\omega =\frac{\pi N}{30}$ | (5) |
装置运行时转子受到高压盐水和低压海水两股流体的冲击,且两股流体对转子的冲击力矩可被视为相同,所以转子受到的动力矩M1可表示为:
| ${{M}_{1}}=2Fr=2\rho rkQ\frac{kQcot\theta }{3{{A}^{*}}}-\frac{\pi rN}{30}$ | (6) |
M1的方向与转子转动方向相同。公式(6)给出了转子所受动力矩与其转速的关系式,可以看出随着转速的增大,动力矩M1呈减小的趋势;建立了转子动力矩与流体流量的关系式,从而完成了流体流量与转子受力之间的过渡。
2.2 转子阻力矩分析转子转动进入稳定阶段后,转子的上下端面与对应端盘端面之间均会形成端面间隙,转子外周面与转子套筒内壁面之间会形成周面间隙。在压力的作用下,高压盐水和低压海水会充满微小的端面间隙和周面间隙从而形成薄层液膜,薄层液膜的形成会对转动的转子形成黏性阻力。故本装置中转子转动时会受到周面阻力矩和端面阻力矩。
2.2.1 转子周面阻力矩图 4为转子外周面与转子套筒内壁面间润滑液层俯视图,其中转子外径2R4,套筒的内径2R6。

|
| 图 4 润滑液层俯视图 Figure 4 Top view of lubricant fluid layer |
| |
转子转动时受到的周面阻力可由牛顿黏性定律表达[16]。
| $f=\mu S\frac{d{{V}_{R}}}{dR}\text{ }$ | (7) |
半径R处的润滑液层满足
| ${{V}_{R}}=\omega R$ | (8) |
图 5给出了转子外周面与转子套筒内壁面间润滑液层的正视图,转子外周面开有一内径2R5,宽L2的环槽,实验时可将测速用反光纸贴于此处,为了便于讨论将此环槽定义为转子反射段,将转子剩余部分定义为转子非反射段,非反射段宽度为L1(L1=L-L2)。

|
| 图 5 润滑液层正视图 Figure 5 Front view of lubricant fluid layer |
| |
对于长度为L1的非反射段,其表面积为:
| ${{S}_{1}}=2\pi {{R}_{4}}{{L}_{1}}$ | (9) |
转子周面润滑液体形成的黏性力矩为:
| $M{{\prime }_{2}}={{R}_{4}}f$ | (10) |
将公式(7)、(8)和(9)代入公式(10)并计算得:
| $M{{\prime }_{2}}=2\pi \mu {{R}_{4}}^{2}{{L}_{1}}\left( R\frac{d\omega }{dR}+\omega \right)$ | (11) |
此方程的边界条件为:R=R6,ω=0;R=R4,ω=πN30。对式(11)分离变量积分处理得到:
| $M{{\prime }_{2}}=\frac{{{\pi }^{2}}\mu {{L}_{1}}R_{_{4}}^{^{3}}}{15\left( {{R}_{6}}-{{R}_{4}} \right)}N$ | (12) |
同理可求长度为L2的反射段受到的阻力矩:
| $M{{\prime\prime }_{2}}=\frac{{{\pi }^{2}}\mu {{L}_{2}}R_{_{5}}^{^{3}}}{15\left( {{R}_{6}}-{{R}_{5}} \right)}N$ | (13) |
所以转子受到的周面阻力矩:
| ${{M}_{2}}=M{{\prime }_{2}}+M{{\prime\prime }_{2}}=\frac{{{\pi }^{2}}\mu {{L}_{1}}R_{_{4}}^{^{3}}N}{15\left( {{R}_{6}}-{{R}_{4}} \right)}+\frac{{{\pi }^{2}}\mu {{L}_{2}}R_{_{5}}^{3}N}{15\left( {{R}_{6}}-{{R}_{5}} \right)}$ | (14) |
M′2、M″2以及M2的方向均与转子转动方向相反。公式(14)给出了转子所受周面阻力矩与其转速的关系式,可以看出随着转速的增大,周面阻力矩M2呈增大的趋势。
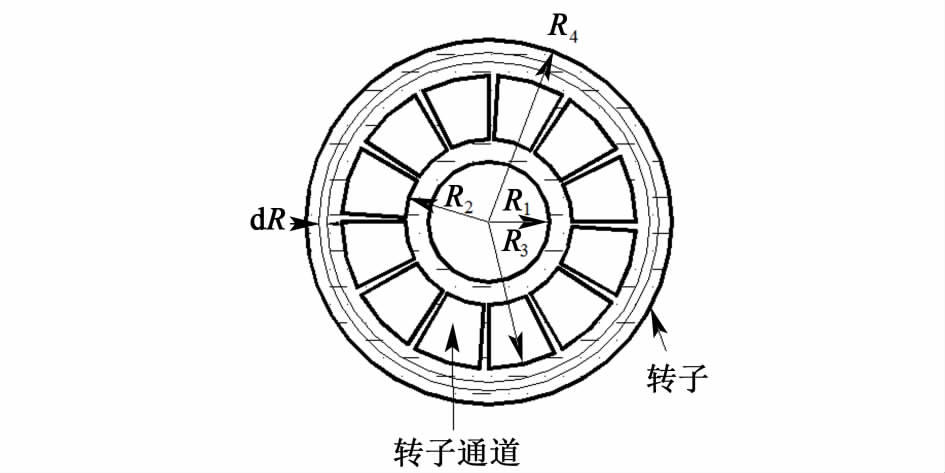
2.2.2 转子端面阻力矩图 6为转子的俯视图。本研究2.2.1小节用微元法求出了转子周面所受的阻力矩M2,转子端面所受的阻力矩M3可用同样的方法表达:
| $\begin{matrix} {{M}_{3}}=\int _{_{{{R}_{1}}}}^{^{{{R}_{2}}}}\mu \omega R\cdot 2\pi RdR+\int _{_{{{R}_{2}}}}^{^{{{R}_{3}}}}\mu \omega R(2\pi R-12\alpha R)dR \\ +\int _{_{{{R}_{3}}}}^{^{{{R}_{4}}}}\mu \omega R\cdot 2\pi RdR \\ \end{matrix}$ | (15) |
|
| 图 6 转子俯视图 Figure 6 Top view of rotor |
| |
将公式(5)代入公式(15)并计算得:
| ${{M}_{3}}=\frac{{{\pi }^{2}}\mu N}{45}\left( R_{_{4}}^{^{3}}-R_{1}^{^{3}} \right)-\frac{2\pi \alpha \mu N}{15}\left( R_{_{3}}^{3}-RX_{_{3}}^{^{3}} \right)$ | (16) |
M3的方向与转子转动方向相反。公式(15)给出了转子所受端面阻力矩与其转速的关系式,可以看出随着转速的增大,端面阻力矩M3呈增大的趋势。
2.3 转子转速计算当转子转动进入稳定阶段后转子合外力矩:
| $Mz={{M}_{1}}-{{M}_{2}}-2{{M}_{3}}=0\text{ }$ | (17) |
将式(6)、(14)、(16)代入式(17)整理有:
| $N=\frac{B{{Q}^{2}}}{CQ+D}$ | (18) |
其中,
| $B=\frac{2\rho r{{k}^{2}}cot\theta }{{{3600}^{2}}{{A}^{*}}}$ | (19) |
| $C=\frac{\pi \rho k{{r}^{2}}}{18000\text{ }}$ | (20) |
| $\begin{align} & D=\frac{{{\pi }^{2}}\mu }{5}\frac{{{L}_{1}}}{{{R}_{6}}-{{R}_{4}}}R_{_{4}}^{^{3}}+\frac{{{\pi }^{2}}\mu }{5}\frac{{{L}_{2}}}{{{R}_{6}}-{{R}_{5}}}R_{5}^{3} \\ & +\frac{2{{\pi }^{2}}\mu }{15}\left( R_{4}^{3}-R_{_{1}}^{^{3}} \right)-\frac{4\pi \mu \alpha }{5}\left( R_{_{3}}^{3}-R_{_{2}}^{^{3}} \right) \\ \end{align}$ | (21) |
由公式(18)~(21)可以看出,在流动系统里能影响装置转速的因素有系统流量Q、导流结构末端冲击角度θ、有效冲击系数k等。由于实际工程中应用较多的是变量Q,所以本实验部分以Q为变量,探究其对转速的影响。
将公式(19)~(21)中涉及的装置结构参数测出,结果如表 1所示。将装置结构参数值以及其他参量值代入公式(18)可得适用于本套实验装置的转速与流量之间的理论关系:
| $N=\frac{0.0395{{Q}^{2}}}{0.000132Q+0.002028}$ | (22) |
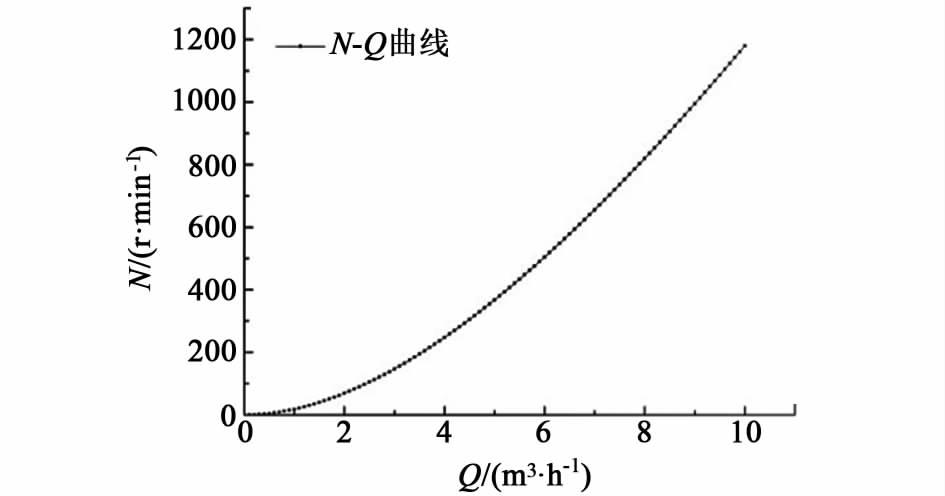
将公式(22)反映出来的转速与流量关系制成N-Q曲线,如图 7所示。
|
| 图 7 理论转速变化曲线 Figure 7 Curve of theoretical rotating speed |
| |
由图 7可以看出:当Q=0时,N=0;随着流量的增大,转速呈增大趋势,且增幅不断。
3 实验部分为了对公式(22)的准确性进行验证,本研究在低压环境下测定了转速随流量的变化关系。
3.1 实验装置及测试流程实验装置中的转子依靠流体水力冲击转动,故本实验采用定制的激光测速仪实现转子转速的非接触测量。为配合测量过程,装置外筒体选用透光性能比较好的有机玻璃材料。装置高压盐水入口压力限制为0.5 MPa。
将转芯和其它零部件安装在外筒体中,连接好管路组成如图 8所示的实验系统。全开高低压进口管路旁路阀,依次开启低压泵、高压泵,排气。依次调节低压海水入口、高压盐水入口流量至4.4 m3·h-1,缓慢关闭增压盐水出口阀门调节高压盐水入口压力至0.5 MPa。观察转速Ne变化,待其稳定后进行转速记录。将低压海水入口、高压盐水入口流量依次调至5.0、6.0以及7.1 m3·h-1,重复上述实验。

|
| 图 8 实验装置示意图 Figure 8 Schematic diagram of experimental set-up |
| |
实验结果如图 9所示。

|
| 图 9 实验转速变化曲线 Figure 9 Curve of experimental rotating speed |
| |
当高、低压入口流量为4.4 m3·h-1,装置转速Ne为285 r·min-1;当流量为7.1 m3·h-1,转速Ne增至600 r·min-1。随着流量的增大,转速在增大。
4 理论值与实验值对比由图 7和图 9发现,理论转速曲线和实验转速曲线反映的变化规律一致,即随着系统流量的增大,理论转速与实验转速均呈增大的趋势。为了进一步对理论转速和实验转速进行对比,将4个实验流量值下的理论转速值和实验转速值列出如表 2所示。
由表 2发现,当流量处于4.4~7.1 m3·h-1区间内时,理论转速略大于实验转速。本研究在推导转速理论公式的过程中,曾作出如下2个假设:1)由于螺旋导流结构末端的坡度比较平缓,故假设3#~5#通道所对应的冲击角度相同。实际上3#~5#通道所对应的冲击角度并不相等,其大小关系为θ3#>θ4#>θ5#,此处θ3#代表 3#通道所对应的冲击角度,其它两个意义与此相同。此假设相当于减小了进入3#和4#通道的流体的冲击角度,使得冲击转子转动的流体流量偏大,从而使转子理论转速偏大;2)忽略了螺旋导流结构与转子之间的端面间隙泄露量,从而也使得冲击转子转动的流体流量偏大,转子理论转速也会偏大。
| 实验流量Q/(m3·h-1) | 实验转速Ne/(r·min-1) | 理论转速Nt/(r·min-1) | 转速差ΔN=Nt-Ne/(r·min-1) | 相对误差 |
| 4.4 | 285 | 293 | 8 | 2.81 |
| 5.0 | 330 | 367 | 37 | 11.21 |
| 6.0 | 450 | 504 | 54 | 12.00 |
| 7.1 | 600 | 671 | 71 | 11.83 |
公式(18)和(19)中的k值是从对本套实验装置的数值模拟中计算出来的,模拟模型与实际装置之间存在差别,导致k值的选取可能也会使理论转速大于实验转速;除此之外公式(18)、(19)和(20)中的θ以及装置相关结构参数都是通过测量得到,受测量工具精度的影响,这些装置参数的数值可能也会使理论转速大于实验转速。
虽然如此,由表 2发现除Q=4.4 m3·h-1外,其它3种系统流量下对应的理论转速与实验转速之间相对误差比较稳定,均保持在12%左右,说明公式(18)在推导上具有一定的合理性。
5 结论1) 启动过程中,随着转速的增加,转子因流体水力冲击而产生的动力矩不断减小,因流体黏性阻力而产生的阻力矩不断增大,导致所受的合外力矩不断减小。当合外力矩值为0时,转子的转速趋于稳定。
2) 随着系统流量的增大,转子的理论转速和实验转速均呈增大的趋势。
3) 4个实验流量下由理论公式算出的理论转速与实验转速相对误差最大为12%,说明理论公式可以为水力自驱旋转式能量回收装置的结构优化设计、操作条件的规范等提供一定的理论依据。
符号说明:
A*—单个流体通道的横截面积,m2;
B、C、D—转子结构参数;
dVR/dR—润滑液层半径R处速度梯度,s-1;
F—流体冲击转子孔道的切向作用力,N;
f—转子转动所受周面黏性阻力,N;
k—有效冲击系数;
L—转子高度,m;
L2—转子反射段宽度,m;
L1—转子非反射段宽度,m;
M1—转子受到的动力矩,N·m;
M′2——转子非反射段所受阻力矩,N·m;
M″2—转子反射段所受阻力矩,N·m;
M2—转子所受周面阻力矩,N·m;
M3—转子所受端面阻力矩,N·m;
Mz—转子所受合外力矩,N·m;
N—转子转速,r/min;
Ne—实验转速,r/min;
Nt—理论转速,r/min;
Q—装置处理的流体体积流量,m3·h-1;
Qbi—高压盐水入口流体流量,m3·h-1;
Qsi—低压海水入口流体流量,m3·h-1;
R1—转子中心孔半径,m;
R2—转子通道小环半径,m;
R3—转子通道大环半经,m;
R4—转子半径,m;
R5—转子反射段半径,m;
R6—套筒内孔半径,m;
r—流体通道中心截面处的半径,m;
2R5—环槽内径,m;
S—转子的周面面积,m2;
S1—转子非反射段面积,m2;
Vz—驱动流体平均轴向速度,m·s-1;
Vr—驱动流体水平切向速度,m·s-1;
VR—润滑液层半径R处的线速度,m·s-1;
α—转子通道周向跨度,rad;
ρ—流体密度,kg·m-3;
ω—流体冲击转子后的残余角速度,rad·s-1;
θ—流体在导流结构末端的冲击角度,°;
θ3#—3#通道所对应的冲击角度,°;
θ4#—4#通道所对应的冲击角度,°;
θ5#—5#通道所对应的冲击角度,°;
|η|—理论转速与实验转速的相对误差;
μ—流体黏性系数,Pa·s。
| [1] | Peñate B, García-Rodríguez L. Current trends and future prospects in the design of seawater reverse osmosis desalination technology[J]. Desalination,2012 : 1–8 |
| [2] | Pe?ate B, de la Fuente J A, Barreto M. Operation of the RO kinetic energy recovery system: Description and real experiences[J]. Desalination,2010,252 (1/3) : 179–185 |
| [3] | 刘宁, 李艳霞, 刘中良,等. 反渗透海水淡化系统中压力能回收装置[C]//中国高等教育学会工程热物理专业委员会.高等学校工程热物理第十九届全国学术会议论文集. 郑州,2013 |
| [4] | 王颖, 张妍, 伍联营, 等. 旋转式压力能交换器的数值模拟[J]. 计算机与应用化学,2014,31 (1) : 29–32 Wang Ying, Zhang Yan, Wu Lianying, et al. Numerical simulation of rotary pressure exchanger[J]. Computers and Applied Chemistry,2014,31 (1) : 29–32 |
| [5] | 王越, 余瑞霞, 徐世昌, 等. 正位移式阀控能量回收装置盐水连续进料过程特性研究[J]. 水处理技术,2006,32 (1) : 23–25 Wang Yue, Yu Ruixia, Xu Shichang, et al. Studies on brine continuous feeding of positive displacement type valve-controlled energy recovery unit[J]. Water Treatment,2006,32 (1) : 23–25 |
| [6] | Bross S, Kochanowski W, Schuler C. Rotary pressure exchanger: US, 20070104588[P]. 2007-01-01 |
| [7] | Martin J, Stover R L. Rotary pressure transfer device: US, 8075281B2[P]. 2011-12-13 |
| [8] | Pique G G, Stover R L, Martin J G, et al. Rotary pressure transfer device with improved flow: US, 7997853B2[P]. 2011-08-16 |
| [9] | Hauge, Leif. Pressure exchanger: US, 7306437B2[P]. 2007-12-11 |
| [10] | Hauge L J. New XPR technology expands ERD market potential[J]. The International Desalination & Amp; Water Reuse Quarterly,2011,21 (2) : 32–35 |
| [11] | Stover R L. Development of a fourth generation energy recovery device[C]//American Society of Mechanical Engineers. ASME 2004 International Mechanical Engineering Congress and Exposition, 2004:195-200 |
| [12] | 张金鑫, 王越, 杨勇君, 等. 反渗透海水淡化转子式压力交换器运行特性研究[J]. 化学工业与工程,2012,29 (5) : 48–52 Zhang Jinxin, Wang Yue, Yang Yongjun, et al. Operating characteristics of rotary pressure exchanger for SWRO desalination system[J]. Chemical Industry and Engineering,2012,29 (5) : 48–52 |
| [13] | 杨勇君, 王越, 张金鑫, 等. 旋转式能量回收装置混合过程优化研究[J]. 化学工业与工程,2012,29 (6) : 42–49 Yang Yongjun, Wang Yue, Zhang Jinxin, et al. Simulation and optimization on the mixing performance of rotary energy recovery device[J]. Chemical Industry and Engineering,2012,29 (6) : 42–49 |
| [14] | 卢彦越. 反渗透海水淡化系统优化设计的研究[D]. 山东青岛: 中国海洋大学, 2004 |
| [15] | 韩松, 王越, 许恩乐, 等. 水力驱动转子式能量回收装置启动特性研究[J]. ,2014,31 (2) : 24–30 Han Song, Wang Yue, Xu Enle, et al. Startup characteristics of hydraulic-drive rotary energy recovery device[J]. Chemical Industry and Engineering,2014,31 (2) : 24–30 |
| [16] | 童刚, 陈丽君, 冷健. 旋转式黏度计综述[J]. 自动化博览,2008,24 (1) : 68–70 Tong Gang, Chen Lijun, Leng Jian. A review on rotary viscometer[J]. Automation Panorama,2008,24 (1) : 68–70 |
 2016, Vol. 33
2016, Vol. 33





