在各种换热设备中,管壳式换热器具有结构简单、可靠性高、使用压力范围广、使用技术成熟等优点。因此,管壳式换热器广泛应用于石油、化工、轻工、冶金等过程工业以及其他工业部门[1-2]。目前,螺旋折流板换热器逐步被人们所认可,相比于传统的弓形折流挡板换热器它有极大的优势:1)增强了壳程换热;2)通过壳程时压降更低;3)减少了旁通流;4)降低了壳程污垢热阻和流激振动[3]。过去数十年间,为了满足对螺旋折流板换热器的精确设计,人们在实验和数据研究方面做了大量的研究,提出了许多有效数据以及壳程传热和压降的关联方法[4-9]。
近年来,人工神经网络作为一种新兴的优选方法,成功地应用于许多科学研究和工程实践。特定的人工神经网络被用来处理多种换热器在稳态传热和水力学特性的分析、性能预测和动态控制等领域,并取得了不错的效果。Diaz等[10]在使用人工神经网络对单排管翅式换热器进行稳态以及动态模拟控制上开展了一系列工作。Pacheco-Vega等[11]利用神经网络对冷冻系统使用非常普遍的以空气和R22冷冻剂作为工作介质的换热器的总换热速率进行了模拟。Islamoglu等[12]在对管芯式换热器进行换热速率实验基础上,利用神经网络与反向传播算法结合建立了预测模型。Hao等 [13]对5种不同结构参数的板翅式换热器一定雷诺数范围内的换热系数j因子和摩擦系数f因子进行了实验研究,利用所得到的40组有限实验数据建立了板翅式换热器j因子和f因子的预测模型。但是大多数研究都集中于管翅式换热器,只有Xie等[14]将人工神经网络应用到了对弓形板管壳式换热器和连续型螺旋折流板管壳式换热器换热性能的预测分析上。在螺旋折流板换热器壳程换热和流体力学方面的分析,人工神经网络还没有大规模应用。
因此,本研究利用中试试验所得到的光滑管和横槽管非连续螺旋折流板换热器壳程换热系数与压降数据,建立了9个输入参数的采取遗传算法优化的多层感知器神经网络预测模型,比较了遗传算法优化与否的预测误差以及训练预测过程中的误差,并将其泛化能力与回归关联式进行了对比。将试验与模拟所得到的数据结合,进一步地对模型进行训练,建立了适用范围更广的螺旋折流板换热器壳程换热系数与压降预测模型。
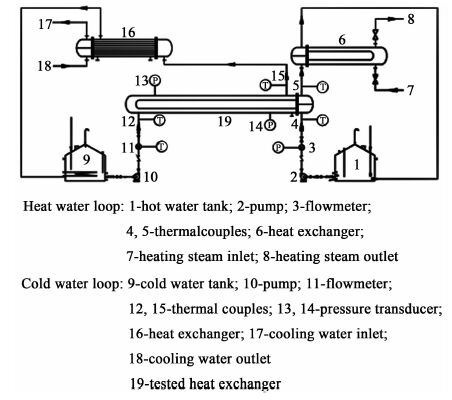
1 螺旋折流板换热器中试试验螺旋折流板换热器中试试验装置流程图如图 1所示。系统包括2个独立的循环:冷却工作介质及加热工作介质循环系统,建立了管壳式换热器中试试验平台对3台螺旋角分别为7°、13°和25°的螺旋折流板管壳式换热器的壳程流阻和传热特性进行研究。此外中试试验中采用了2种类型的换热管,分别是普通光管和横槽换热管,测试了2种换热管对于壳程传热与流阻性能的影响。螺旋折流板换热器的结构参数见表 1。利用中试试验所得到的光滑管和横槽管螺旋折流板换热器壳程换热系数与压降数据,建立采取遗传算法优化的多层感知器神经网络预测模型。
|
| 图 1 中试试验系统流程图 Figure 1 Experimental system schematic |
| |
| 参数 | 数值 |
| 壳体内径/mm | 500 |
| 换热管外径/mm | 19 |
| 换热管内径/mm | 15 |
| 换热管排列方式 | 正方形 |
| 换热器长度/mm | 6 000 |
| 换热管数量/个 | 208 |
| 管间距/mm | 25 |
| 进口直径/mm | 150 |
| 出口直径/mm | 150 |
试验过程中,壳程入口体积流量取值范围设置为50~150 m3/h。管程入口体积流量取值范围设置为50~90 m3/h。
2 多层感知器优化模型的参数选择本研究建立的多层感知器预测模型是在利用Matlab2010A软件中的神经网络工具包基础上编程实现的。所建立的网络结构中,输入层中包含9个独立变量,分别是壳程体积流量Vs、管程体积流量Vt、壳程流体进口温度Ts、管程流体进口温度Tt、螺旋角β、螺距B、螺旋周期数S、管子槽深e和槽距tp。其中,壳程与管程工作介质都是水,壳程入口温度40~60 ℃,管程入口温度70~90 ℃,其余输入变量的取值范围见表 2。输出层包含有2个输出变量,分别是壳程换热系数和壳程压降,是评价换热器性能的主要指标。
| 螺旋角β/(°) | 螺距B/mm | 螺旋周期数S | 管子槽深e/mm | 槽距tp/mm |
| 7 | 36.25 | 38 | 0 | 0 |
| 7 | 36.25 | 38 | 2 | 10 |
| 13 | 77.60 | 17 | 0 | 0 |
| 13 | 77.60 | 17 | 2 | 10 |
| 25 | 159.70 | 8 | 0 | 0 |
| 25 | 159.70 | 8 | 2 | 10 |
将换热器中试试验中得到的562组实验数据按比例随机分成3组,其中的60%用来训练网络,20%用于验证网络的过拟合性,20%用于测试网络性能,即它的泛化能力。多层感知器模型隐含层传递函数设为Sigmoid函数,输出层传递函数设为线性函数。为了有效的训练网络,将输入输出变量统一归一化到[0.15,0.85]范围。训练过程中采用了Levenberg-Marquardt (TRAINLM)函数作为训练函数。验证过程最大迭代失败次数设为20次,学习速率设定为0.01。为了有效地评价多层感知器模型对于壳程换热系数以及压降训练与预测时的误差,选择平均相对误差作为评价标准,按公式(1)计算:
| $MRE=\frac{1}{M}\sum _{i=1}^{M}\left| \frac{{{A}^{e}}-{{A}^{p}}}{{{A}^{e}}} \right|~$ | (1) |
其中Ae是实验结果,Ap是预测结果,M是数据总数。
网络的预测能力,即泛化能力通过预测输出值和实验值之间的平均准确度R和分散度σ来比较。
| $R=\frac{1}{N}\sum _{i=1}^{N}{{R}_{i}}=\frac{1}{N}\sum _{i=1}^{N}\frac{{{A}^{e}}}{{{A}^{p}}}$ | (2) |
| $\sigma =\sqrt{\sum _{i=1}^{N}\frac{{{(R-{{R}_{i}})}^{2}}}{N}}$ | (3) |
对于用来优化多层感知器网络的遗传算法,选择预测值和给定输出值之间的平均相对误差的绝对值之和作为其适应度函数,计算方法如公式(4)。
| $F=\sum _{i=1}^{M}\left| \frac{{{A}^{e}}-{{A}^{p}}}{{{A}^{e}}} \right|~$ | (4) |
在遗传算法的优化过程中,操作选择轮盘赌算法,种群规模设为40,进化次数设为200,交叉操作和变异操作的概率分别设置为0.4和0.1。
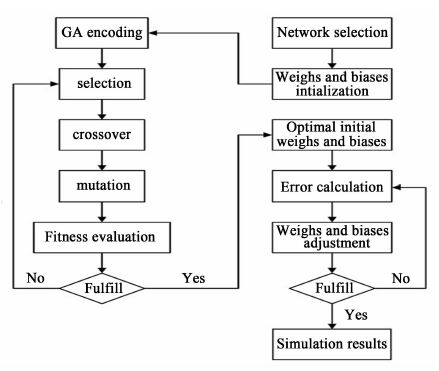
利用遗传算法优化多层感知器神经网络模型的流程如图 2所示。
|
| 图 2 遗传算法优化多层感知器模型流程 Figure 2 Procedures of the MLP network optimization with the genetic algorithm |
| |
图 3显示的是遗传算法优化多层感知器网络过程中的适应度值变化。采用的网络结构是9-7-5-2,即一层7个节点的第一隐含层,一层5个节点的第二隐含层。在初始阶段,适应度值很大,说明当前种群所代表的初始权值与阀值设置不适应所建立的网络,会引起较大的训练及预测误差。随着这些种群个体在前期进化过程中被不断淘汰,误差总和开始迅速下降,到一定进化步骤之后逐渐变化为阶梯型下降,在大约110步之后,曲线开始变得平缓,并且达到其最小值,说明优化过程结束。

|
| 图 3 适应度值变化曲线 Figure 3 The process of evolution |
| |
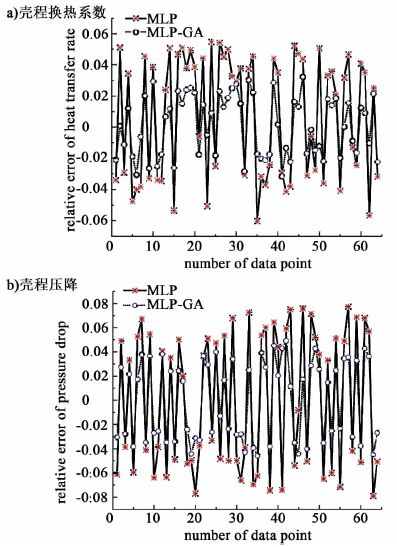
图 4a)和图 4b)显示的是经过优化的多层感知器模型(MLP-GA)与未经优化的模型(MLP)在对换热器壳程换热系数和压降进行预测时的相对误差分布图。红色星号代表的是未经优化的多层感知器神经网络,而蓝色圆圈代表的是经过遗传算法优化后的多层感知器模型。
|
| 图 4 对换热器壳程换热系数和压降进行预测时的相对误差分布图 Figure 4 Relative error scatter of and between the predictions and experiment data |
| |
从图 4中可以看出,经过优化的网络模型显示出了更高的预测精确度和稳健性,克服了初始权值与阀值的随机选择对其预测能力造成的影响。虽然采取遗传算法进行优化会减慢多层感知器网络的训练速度,但是这种优化策略能够使模型预测能力得到显著增强。因此接下来所采用的不同结构的多层感知器网络均使用遗传算法进行优化。
3.2 遗传算法优化的多层感知器模型训练预测结果本研究选择7种多层感知器模型网络结构对实验数据进行训练与测试,表 3和表 4分别显示的是这7种不同网络结构模型对壳程换热系数和压降的预测结果。从表 3和表 4中可以发现,对于单隐含层网络,当节点数从5增加到7时,训练过程的平均相对误差值(MRE)发生下降,这说明隐含层内节点数的适当增加能够提高训练过程的准确度。而对于双隐含层网络,当第一隐含层节点数由6增加到8的时候,预测输出值和实验值之间的平均准确度(R)和分散度(σ)并没有随之降低,所以单纯地提高节点数不一定意味着网络预测性能的提高。尽管9-8-5-2的网络结构训练过程中的MRE值最低,但是泛化能力表现却不是最好的。而9-7-5-2网络结构训练过程对于壳程换热系数以及压降预测的平均相对误差分别为1.0012%和2.0423%,虽然不是最好的,但是其测试过程R分别为1.0143和1.0291,σ分别为0.0605和0.0956,是所有网络结构中最低的,说明其泛化能力是最好的。因此,在预测本试验螺旋折流板换热器壳程换热系数和壳程压降的多层感知器模型中,9-7-5-2是最佳的网络结构。
| 网络结构 | 训练误差 | 测试误差 | |
| MRE/% | R | σ | |
| 9-5-2 | 2.5945 | 1.0223 | 0.0987 |
| 9-6-2 | 2.3512 | 1.0208 | 0.1004 |
| 9-7-2 | 2.0783 | 1.0281 | 0.0973 |
| 9-6-5-2 | 1.1526 | 1.0196 | 0.0872 |
| 9-7-5-2 | 1.0012 | 1.0143 | 0.0605 |
| 9-8-5-2 | 0.9924 | 1.0184 | 0.0781 |
| 9-7-4-2 | 1.1201 | 1.0176 | 0.0986 |
| 关联式 | 6.0823 | 1.0608 | 0.2136 |
| 网络结构 | 训练误差 | 测试误差 | |
| MRE/% | R | σ | |
| 9-5-2 | 4.2342 | 1.0552 | 0.1633 |
| 9-6-2 | 3.7164 | 1.0486 | 0.1578 |
| 9-7-2 | 3.3038 | 1.0411 | 0.1546 |
| 9-6-5-2 | 2.3205 | 1.0345 | 0.1217 |
| 9-7-5-2 | 2.0423 | 1.0291 | 0.0956 |
| 9-8-5-2 | 2.0189 | 1.0338 | 0.1125 |
| 9-7-4-2 | 2.1636 | 1.0356 | 0.0975 |
| correlation | 10.2873 | 1.1029 | 0.3321 |
图 5a)和图 5b)显示的是由经过优化的多层感知器模型训练过程所预测的壳程换热系数与压降值同实验值的对比。

|
| 图 5 优化的多层感知器模型训练过程预测值与实验值对比 Figure 5 Prediction of shell-side heat transfer rate and pressure drop by the MLP-GA with training data |
| |
由图 5可以看到,大部分训练过程的预测输出值都非常接近于对角线,即训练过程预测输出值与实验值接近一致。
由于多层感知器模型最重要的是其泛化能力,即对于训练数据范围以外数据预测的准确度,因此不仅要求其对于训练数据预测准确度,更要考察其对于测试数据预测的准确度。
图 6a)和图 6b)显示的是经过优化的多层感知器模型测试阶段所预测的壳程换热系数与压降值同实验值的对比。可以发现,基本上预测输出值都很接近对角线,说明预测输出值与实验值接近一致,证明了我们所建立的遗传算法优化的多层感知器网络在预测螺旋折流板换热器壳程换热系数和压降时具有良好的泛化能力。

|
| 图 6 优化的多层感知器模型测试过程预测值与实验值对比 Figure 6 Prediction of shell-side heat transfer rate and pressure drop by the MLP-GA with testing data |
| |
将中试试验所得到的螺旋折流板换热器水-水试验数据做回归处理得到努赛尔数(Nu)及摩擦因子(f),形如Nu=CRemPr1/3以及f=φReω的关联式,适用范围是8000<Re<12000,2.4<Pr<4.1。壳程进口温度为40 ℃,管程进口温度为70 ℃时,3种不同螺旋角的关联式如下所示:
| $7{}^\circ :Nu=0.1881R{{e}^{0.5307}}P{{r}^{1/3}},f=0.462R{{e}^{-0.226}}$ | (5) |
| $13{}^\circ :Nu=0.2926R{{e}^{0.5009}}P{{r}^{1/3}},f=2.0807R{{e}^{-0.371}}~$ | (6) |
| $25{}^\circ :Nu=0.5647R{{e}^{0.4456}}P{{r}^{1/3}},f=2.9973R{{e}^{-0.427}}$ | (7) |
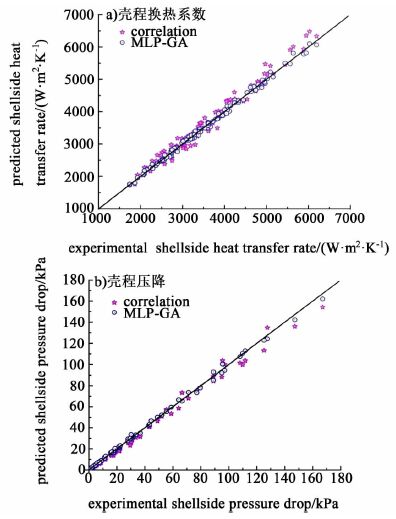
图 7a)和图 7b)显示的是优化的多层感知器预测模型同壳程进口温度为40 ℃时的回归关联式在预测精度上的对比。
|
| 图 7 优化的多层感知器网络和关联式预测精度对比 Figure 7 Comparison of shell-side heat transfer rate and pressure drop predictions by the MLP-GA and correlations |
| |
由图 7可以看出,不管是对于壳程换热系数还是壳程压降,回归关联式计算结果与真实值相差较大。而利用多层感知器预测模型所得到的预测结果具有很好的精确度。
从表 3和表 4中也可以看出,回归关联式所得到的计算结果精确度要远远低于我们所测试的所有结构类型的多层感知器预测网络。
此外,通过多层感知器预测网络能够直接利用输入变量的数值得到对应的壳程换热系数和压降,而关联式需要先计算出壳程传热Nu数以及摩擦因子f,然后再将其转化为壳程换热系数以及压降值。因此,不管是从预测的准确度,还是方便性来讲,多层感知器预测网络与回归关联式相比,都具有很大优势。
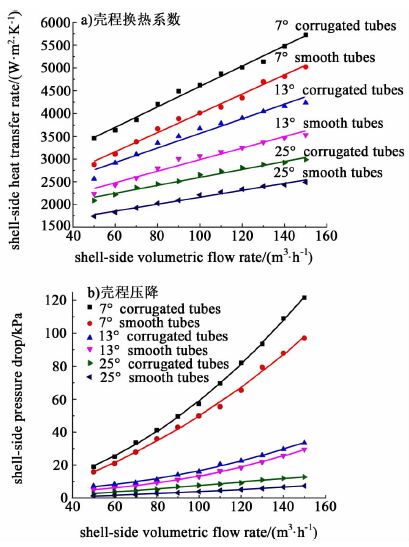
本研究建立的遗传算法优化的多层感知器模型(MLP-GA)可以用来预测输入参数对输出的影响。图 8a)和图 8b)显示使用MLP-GA方法在训练数据范围对换热器壳程不同体积流量下的壳程换热系数及壳程压降的预测。
|
| 图 8 遗传算法优化的多层感知器模型预测不同体积流量下换热器壳程换热系数及壳程压降 Figure 8 Predictions for shell-side heat transfer rate and pressure drop vs. shell-side volumetric flow rate by MLP-GA |
| |
由图 8可以看出,6种型式换热器的壳程换热系数均随体积流量的增加而增大,同一体积流量下,螺旋角越小,壳程换热系数越高。在相同螺旋角下,横槽管换热器的壳程换热系数较光滑管高。相同体积流量下,7°螺旋角换热器壳程压降明显高于其他几种型式。相同螺旋角的情况下,横槽管换热器壳程压降均高于光滑管换热器。壳程传热系数及壳程压降的网络预测值与实验值规律一致。
4 结论通过换热器中试试验平台考察了不同螺旋角横槽管和光滑管螺旋折流板换热器的壳程性能,利用中试试验数据建立了预测螺旋折流板换热器壳程换热系数与压降的多层感知器神经网络模型,并利用遗传算法对多层感知器预测模型进行了优化,得到以下结论。
1) 遗传算法优化的多层感知器模型预测精度要高于未经优化的模型,遗传算法优化能够提高多层感知器模型的预测准确度和稳健性,克服了初始权值和阀值随机选择的不利影响。
2) 多层感知器模型的网络结构要根据实际应用中的预测精度来进行选择。经过比较,我们选择了训练误差和泛化性能综合起来最好的9-7-5-2的网络结构,此结构训练过程对于壳程换热系数和压降预测的平均相对误差分别为1.0012%和2.0432%,测试过程预测的平均准确度为1.0143和1.0291,分散度为0.065和0.0956。
3) 遗传算法优化的多层感知器网络模型的预测精度要高于回归关联式。
4) 采用遗传算法优化的多层感知器模型(MLP-GA)预测体积流量对壳程换热系数及壳程压降的影响。壳程换热系数均随体积流量的增加而增大,且螺旋角越小,壳程换热系数越高,横槽管换热器的壳程换热系数较光滑管高。7°螺旋角换热器壳程压降明显高于13°和25°,横槽管换热器壳程压降高于光滑管换热器。
| [1] | Master B, Chunangad K, Boxma A, et al. Most frequently used heat exchangers from pioneering research to worldwide applications[J]. Heat Transfer Engineering,2006,27 (6) : 4–11 |
| [2] | Stehl K P, Wadekar V V. Different strategies to improve industrial heat exchange[J]. Heat Transfer Engineering,2002,23 (6) : 36–48 |
| [3] | Chen G, Wang Q. Experimental and numerical studies of shell-and-tube heat exchangers with helical baffles[J]. ASME,2009 : 601–609 |
| [4] | Jafari N M R, Shafeghat A. Fluid flow analysis and extension of rapid design algorithm for helical baffle heat exchangers[J]. Applied Thermal Engineering,2008,28 (11/12) : 1324–1332 |
| [5] | Kral D, Stehlik P, Van Der Ploeg H, et al. Helical baffles in shell-and-tube heat exchangers, Part I: Experimental verification[J]. Heat Transfer Engineering,1996,17 (1) : 93–101 |
| [6] | Lei Y, He Y, Chu P, et al. Design and optimization of heat exchangers with helical baffles[J]. Chemical Engineering Science,2008,63 (17) : 4386–4395 |
| [7] | Lutcha J, Nemcansky J. Performance improvement of tubular heat exchangers by helical baffles[J]. Chemical Engineering Research & Design,1990 : 263–270 |
| [8] | Peng B, Wang Q, Zhang C, et al. An experimental study of shell-and-tube heat exchangers with continuous helical baffles[J]. Journal of Heat Transfer,2007,129 (10) : 1425–1431 |
| [9] | Zhang J, Li B, Huang W, et al. Experimental performance comparison of shell-side heat transfer for shell-and-tube heat exchangers with middle-overlapped helical baffles and segmental baffles[J]. Chemical Engineering Science,2009,64 (8) : 1643–1653 |
| [10] | Diaz G, Sen M, Yang K, et al. Dynamic prediction and control of heat exchangers using artificial neural networks[J]. International Journal of Heat and Mass Transfer,2001 : 1671–1679 |
| [11] | Pacheco-Vega A, Sen M, Yang K, et al. Neural network analysis of fin-tube refrigerating heat exchanger with limited experimental data[J]. International Journal of Heat and Mass Transfer,2001,44 (4) : 763–770 |
| [12] | Islamoglu Y, Kurt A, Parmaksizoglu C. Performance prediction for non-adiabatic capillary tube suction line heat exchanger an artificial neural network[J]. Energy Conversion and Management,2005 : 223–232 |
| [13] | Hao P, Xiang L. Neural networks analysis of thermal characteristics on plate-fin heat exchangers with limited experimental data[J]. Applied Thermal Engineering,2009 : 2251–2256 |
| [14] | Xie G, Wang Q, Zeng M, et al. Heat transfer analysis for shell-and-tube heat exchangers with experimental data by artificial neural networks approach[J]. Applied Thermal Engineering,2007,27 (5/6) : 1096–1104 |
 2016, Vol. 33
2016, Vol. 33





