2. 上海中兴派能能源科技有限公司, 上海 201203
2. Shanghai Pylon Technology Company, Shanghai 201203, China
为缓解石油短缺带来的能源危机并保护人类的生存环境,电动汽车(EV)/混合动力汽车(HEV)正在世界范围内获得关注与推广。动力电池组是EV/HEV的关键组成部分。在众多化学电源中,锂离子电池因其比能量密度高、质量轻、充放电循环寿命长等优点成为EV/HEV电池的首选。热管理是延长锂离子电池组使用寿命、维护电池组运行安全的重要手段。受电池材料热稳定性的限制,在高温下电池内部容易发生各种副反应,导致电池寿命大幅降低;在极端条件下,电池组甚至可能发生热失控,从而严重影响电池组运行安全[1]。一般认为,锂离子电池组最适宜的工作温度范围为20~60 ℃,且电池组内的最大温差不应超过5 ℃[2]。因此,一套有效的热管理系统对于电池组的管理来说极其重要。
主动冷却是电池组热管理的一种常用冷却方法,该方法采用空气或液体为冷却介质对电池组进行强制对流冷却。空气冷却系统的优势在于结构简单、运行和维护成本低[3],但该系统无法实现极端条件下电池组的有效热管理。Nelson等[4]的实验表明,当15 mm×100 mm×110 mm方型电池温度超过66 ℃时,采用空冷系统很难将电池温度降低到52 ℃以下。Wu等[5]的模拟以及实验结果也表明在高倍率放电、高环境温度(>40 ℃)条件下,采用空气冷却并不能将电池温度控制在适宜的工作温度范围内。液体的导热系数和比热容均大于空气,在相同流速下其对流换热能力要远高于空气,理论上是一种较好的冷却介质。但液体冷却系统的制造和维护成本高,例如需要保证该系统具有足够好的密封及绝缘设计,这极大制约了其在电池组热管理上的应用[6]。因此,改进空气冷却方法以提高其控温效果可能更容易为电池组热管理系统所接受。
本研究中提出了一种翅片-空气协同冷却的新方法,即将翅片置于电池间隙中,并强迫空气在该间隙中流动以进行散热。采用有限元方法对电池组进行了三维数值模拟。详细分析了翅片-空气协同冷却的控温效果,并将其与传统空气冷却方法的结果进行了对比。对翅片在协同冷却中强化传热的机理也进行了讨论。
1 模型建立过程 1.1 模拟单元的选择锂离子电池组由多个单电池经串并联连接构成,所用单电池可为圆柱形、方型、薄片型等。本研究基于最常见的18650型LiMn2O4/C圆柱形电池构成的电池组,单电池的容量为1 500 mAh。
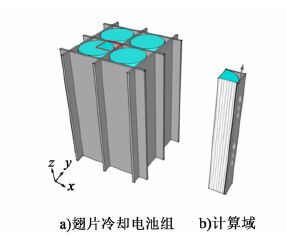
电池组的热管理采用翅片-空气协同冷却法。如图 1a)所示,铝制翅片置于电池间隙中,翅片厚度与电池间距相等,翅片高度与电池高度相等;空气在电池与翅片围成的空隙中流动,与电池及翅片进行热交换从而带走热量。为简化计算,取图 1a)所示电池组中的重复单元[即图 1a)中红线框所示区域]为计算域,如图 1b)所示。因为电池尺寸固定,当改变翅片厚度时,计算域在x,y方向的尺度相应改变。图 1b)中的箭头表示空气流动方向。对传统空气冷却方法进行模拟分析时,模拟单元的选取与图 1b)所示类似,但模拟单元中不考虑翅片的存在,即图 1b)中翅片所占区域由空气域代替。
|
| 图 1 电池组及电池模拟单元示意图 Figure 1 Schematic diagram of battery pack and simulation unit of battery |
| |
圆柱型锂离子电池是由正极集流体、正极活性材料、隔膜、负极活性材料、负极集流体这5层结构叠加卷绕而成的。各层所用材料分别为Al、LiMn2O4、聚丙烯/聚乙烯/聚丙烯3层隔膜、石墨、Cu。由于电解液填充在正负极活性材料及隔膜的孔隙内,正负极活性材料层及隔膜层的导热系数需考虑电解液的影响,其计算方程为[7]:
| ${{\lambda }_{i}}={{\lambda }_{m}}(1-\varepsilon )+{{\lambda }_{f}}$ | (1) |
其中ε表示孔隙率,λm表示未填充电解液的正负极活性材料及隔膜的导热系数,λf表示电解液的导热系数,λi表示填充电解液之后正负极活性材料及隔膜的导热系数,各材料的物性参数见表 1。
| 孔隙率 | 密度/ (kg·m-3) | 比热容/ (J·kg-1·K-1) | 导热系数/ (W·m-1·K-1) | 厚度/ μm | |
| Al | 2 710 | 902 | 237 | 20 | |
| LiMn2O4 | 0.25 | 2 370 | 1 321 | 1.48 | 180 |
| PP/PE/PP | 0.47 | 1 400 | 1 551 | 0.35 | 40 |
| 石墨 | 0.30 | 1 347 | 1 437 | 1.04 | 120 |
| Cu | 8 930 | 386 | 398 | 10 | |
| 电解液 | 1 375 | 1 223 | 0.59 | ||
| 空气 | 1.185 | 1 005 | 0.03 | ||
| 不锈钢 | 7 850 | 475 | 44.5 | 200 |
为简化计算,三维非稳态传热模型中所作的假设为:1) 电池的物性参数不随温度变化;2) 电池内部各处的产热速率相同;3) 电池表面的热辐射量相比于电池热传导量和对流换热量来说很小,可忽略不计;4) 空气的流动视为不可压缩流动。当空气的流速小于1/3声速即风速小于113 m/s时,可认为是不可压缩气体,本研究中空气的流速远小于这个值,故空气的流动视为不可压缩流动[9]。
1.2.1 控制方程电池是该模型中唯一的热源,其在放电过程中产生的热量包括以下两部分:1)电池内阻产生的焦耳热;2)电化学反应的熵变。若以Qb表示电池单位体积的产热速率,则计算公式为[10]:
| ${{Q}_{b}}=\frac{1}{V}\left[ ~I(E-{{E}_{ocv}})-IT\frac{d{{E}_{ocv}}~}{dT}~~ \right]$ | (2) |
其中I、E、Eocv分别代表了电流(放电时I<0,充电时I>0)、电池电压、电池开路电压,Vb代表电池的体积。方程(2)还可以用内阻的形式来表达:
| ${{Q}_{b}}=\frac{1}{{{V}_{b}}}\left[ ~{{I}^{2}}{{R}_{i}}-IT\frac{d{{E}_{ocv}}}{~dT}~ \right]$ | (3) |
其中Ri表示电池的内阻。电池在高倍率放电过程中焦耳热占主导地位,电化学反应熵变可以忽略[11],故本研究中电池的单位体积产热速率可以简化为:
| ${{Q}_{b}}=\frac{\text{ }{{I}^{2}}{{R}_{i}}~}{{{V}_{b}}}$ | (4) |
电池内部存在热传导过程,其能量方程为:
| $\begin{align} & \rho {{C}_{p}}~\frac{\partial {{T}_{h}}}{\partial t}~=\frac{\partial }{\partial x}\left( {{\lambda }_{x,b}}\frac{\partial {{T}_{h}}}{\partial x} \right)+\frac{\partial }{\partial y}\left( {{\lambda }_{x,b}}\frac{\partial {{T}_{h}}}{\partial y} \right)+ \\ & \frac{\partial }{\partial z}\left( {{\lambda }_{x,b}}\frac{\partial {{T}_{h}}}{\partial z} \right)+{{Q}_{b}} \\ \end{align}$ | (5) |
其中ρ、Cp、Qb分别表示电池的平均密度、平均比热容以及单位体积发热功率,λx,b、λy,b、λz,b分别表示电池不同方向上的导热系数,t表示时间,Tb表示电池的温度。为简化模拟过程,不考虑电池内部的层状结构。值得注意的是,各材料的热阻沿电池径向表现为串联关系,沿轴向表现为并联关系,因此电池的导热系数存在各向异性,在径向与轴向应给予分别计算[12],计算方法为:
| $\rho {{C}_{p}}=\frac{\sum{{{\rho }_{i}}{{C}_{p,i}}{{V}_{i}}~}}{\sum{{{V}_{i}}~}}$ | (6) |
| ${{\lambda }_{x,b}}={{\lambda }_{y,b}}=\frac{\sum{{{L}_{i}}~}}{\sum{({{L}_{i}}/{{\lambda }_{i}})}}$ | (7) |
| ${{\lambda }_{z,b}}=\frac{\sum{({{L}_{i}}/{{\lambda }_{i}})}}{\sum{{{L}_{i}}}}$ | (8) |
其中ρi、Cp,i、Vi、Li、λi分别代表锂离子电池中各层的密度、比热容、体积、厚度和导热系数。
翅片内部的能量积累完全由热传导引起,其能量控制方程如式(9):
| ${{\rho }_{f}}{{C}_{p,f}}\frac{\partial {{T}_{f}}}{\partial t}~={{\lambda }_{f}}\frac{\partial {{T}_{f}}}{\partial x}+{{\lambda }_{f}}\frac{\partial {{T}_{f}}}{\partial y}+{{\lambda }_{f}}\frac{\partial {{T}_{f}}}{\partial z}$ | (9) |
其中ρf、Cp,f、λf分别表示翅片的密度、比热容、导热系数,Tf表示翅片的温度。
空气内部的能量积累包括热传导和热对流两部分,其能量控制方程为:
| ${{\rho }_{a}}{{C}_{p,a}}~\frac{\partial {{T}_{a}}~}{\partial t}=\nabla \cdot ({{\lambda }_{a}}\nabla {{T}_{a}})+{{\rho }_{a}}{{C}_{p,a}}{{u}_{a}}\nabla {{T}_{a}}$ | (10) |
其中ρa、Cp,a、λa分别表示空气的密度、比热容、导热系数,Ta表示空气的温度,ua表示空气的流速。
空气在翅片和电池之间的区域流动,质量守恒方程即连续性方程:
| $\nabla {{u}_{a}}=0$ | (11) |
空气的速度控制方程采用不可压缩Navier-Stokes层流流动方程:
| ${{\rho }_{a}}\frac{\partial {{u}_{a}}~}{\partial t}={{\rho }_{a}}{{g}_{a}}-\nabla {{\rho }_{a}}+{{u}_{a}}{{\nabla }^{2}}{{u}_{a}}$ | (12) |
其中ga、Pa表示重力加速度和压强。
1.2.2 初始条件和边界条件 1.2.2.1 初始条件电池、翅片以及空气的初始温度与环境温度相同,为25 ℃:
| ${{T}_{b}}={{T}_{f}}={{T}_{a}}=25(℃)$ | (13) |
空气的初始速度为定值:
| ${{u}_{a}}=constant$ | (14) |
电池与翅片的接触面上,流入该界面的能量等于流出该界面的能量。
| ${{\lambda }_{b}}\nabla {{T}_{b}}={{\lambda }_{f}}\nabla {{T}_{f~}}$ | (15) |
电池与空气的接触面上,流入该界面的能量等于流出该界面的能量。
| ${{\lambda }_{b}}\nabla {{T}_{b}}={{\lambda }_{a}}\nabla {{T}_{a~}}$ | (16) |
电池与空气以及电池与翅片的接触面两侧温度相等。
| ${{T}_{b,surface}}={{T}_{f,surface}}~$ | (17) |
| ${{T}_{b,surface}}={{T}_{a,surface}}$ | (18) |
在整个电池组系统中,电池组上下表面会安置电路板,所以电池以及翅片上下表面近似绝热,即表面上没有能量通过,所以有:
| ${{\lambda }_{b}}\nabla {{T}_{b}}=0$ | (19) |
| ${{\lambda }_{f}}\nabla {{T}_{f~}}=0$ | (20) |
相邻单元与单元之间的接触面为对称性边界,在此边界上能量的净传输量为0。
| ${{\lambda }_{b}}\nabla {{T}_{b}}=0$ | (21) |
| ${{\lambda }_{f}}\nabla {{T}_{f~}}=0$ | (22) |
入口处,空气温度为固定值。
| ${{T}_{a,inlet}}=constant~$ | (23) |
空气进口处为恒定速度边界:
| ${{u}_{a,inlet}}=constant$ | (24) |
空气出口为开放边界,设压强恒定为标准大气压:
| ${{P}_{a}}={{P}_{0}}=101.325(kPa)~$ | (25) |
空气为牛顿型流体,它在电池及翅片表面流动时遵循牛顿黏性定律,其表面流动速度为0。
| ${{u}_{a,surface}}=0$ | (26) |
本研究中,模拟单元内的流场和温度场采用有限元方法进行求解,所用软件为Comsol Multiphysics。运算在联想深腾1800高性能服务器上进行,求解流程如图 2所示。

|
| 图 2 数值计算流程图 Figure 2 Schematic block diagram of numerical calculation |
| |
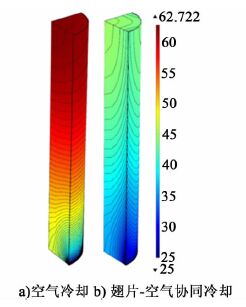
环境温度为25 ℃,7 C放电倍率下,比较了采用空气冷却法、翅片-空气协同冷却法电池放电结束时电池的温度分布情况,结果如图 3所示。
|
| 图 3 空气冷却及翅片-空气协同冷却时电池放电终止时电池的温度分布图(放电倍率7 C,翅片厚度0.5 mm) Figure 3 Temperature distribution of air cooled battery and the fin-air cooled at the end of discharge (discharge rate is 7 C; the thickness of fin is 0.5 mm) |
| |
2种方法中,空气流速均为1 m ·s-1。7 C放电倍率下,采用传统空气冷却法时,电池在放电结束时最大温度达到了62.7 ℃,已超过了电池的正常工作温度范围,如果电池的放电倍率再增大,采用空气冷却法就有可能引发电池热失控。而在采用翅片-空气协同冷却法时,电池的最大温度约为44.9 ℃,相比于传统的空气冷却,电池的最大温度降低了18 ℃,且由图 3可知电池内部温度分布的均匀性也有明显提高。这说明翅片-空气协同冷却方法的散热能力远强于传统空气冷却方法。为了进一步说明翅片-空气协同冷却方法的优势,我们调整了采用传统空气冷却方法时的空气流速,以确保电池最高温降低到与采用翅片-空气协同冷却方法时相同。这时空气流速为15 m ·s-1,是翅片-空气协同冷却时空气流速的15倍;该过程总的送风功率为3.59 W,是翅片-空气协同冷却过程总吹风功率(0.026 W)的136倍。该结果表明翅片-空气协同冷却方法在减少电池组热管理的能耗上具有巨大优势。
电池的放电倍率越高,电池的温度也会越高,翅片-空气协同冷却方法对电池组的控温效果也会有所差异。表 2给出了电池以不同倍率放电完毕时电池的最大温度数据。由表 2可知,随着放电倍率的提高,电池的最大温度也随之升高,但采用翅片-空气协同冷却方法时该温度的升高幅度远小于采用传统空气冷却方法时的幅度。因此,在需要电池进行高倍率放电的场合,如电池应用于混合动力汽车时,采用翅片-空气协同冷却方法将更有效地保障电池组的运行安全。
| 放电倍率/ C | Tmax(空气冷却)/ ℃ | Tmax(翅片-空气 协同冷却)/℃ |
| 4 | 39.7 | 32.2 |
| 5 | 50.3 | 37.8 |
| 6 | 56.2 | 41.7 |
| 7 | 62.7 | 44.9 |
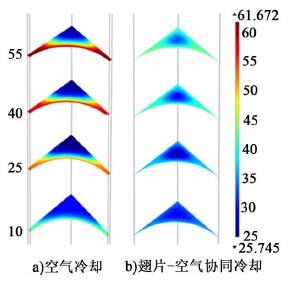
3.1 节的结果表明,与传统空气冷却方法相比,翅片-空气协同冷却方法能更有效地抑制电池的温升。为探究翅片强化传热的机理,在传统空气冷却系统与翅片-空气协同冷却系统的空气流道高度方向上,取电池放电完毕后空气流速截面图和温度截面图并进行对比,如图 4及图 5所示。

|
| 图 4 空气冷却及翅片-空气协同冷却时空气的速度截面图(放电倍率7 C,翅片厚度0.5 mm) Figure 4 The sectional views of the air flow fields in a) the air cooling system b) the fin-air cooling system (discharge rate is 7 C; the thickness of fin is 0.5 mm) |
| |
|
| 图 5 空气冷却及翅片-空气协同冷却时空气温度截面图 (放电倍率7 C,翅片厚度0.5 mm) Figure 5 The sectional views of the air temperature fields in a) the air cooling system b) the fin-air cooling system (discharge rate is 7 C;the thickness of fin is 0.5 mm) |
| |
由图 4和图 5中可知,翅片加入前后,流道中空气的流场发生了改变,进而影响了空气的温度场。在传统空气冷却系统中,热交换仅发生在电池与空气的交界面上,流道中远离该交界面的空气的散热能力并未得到充分利用。而在翅片-空气协同冷却系统中,电池产生的热量传递给翅片后,空气与翅片的交界面上也会发生热交换,即翅片是电池热量传递给空气的媒介。因此与传统空气冷却方法相比,翅片-空气协同冷却方法能够增大传热面积,从而能更有效地抑制电池的温升。
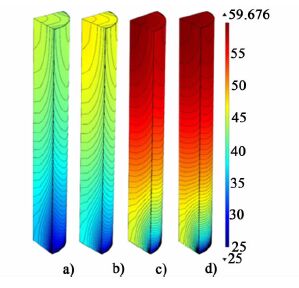
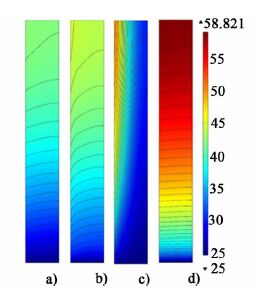
另一方面,电池传导给翅片的热量将从电池-翅片接触面沿翅片厚度、长度及高度方向传导。而翅片在其长度及高度方向上所接触的空气具有不同的温度。根据对流换热原理,翅片与空气的温差越大,在这两者间传热的推动力也就越大。因此在翅片与低温空气的交界面上,翅片向空气传热较快,带走的热量经由翅片内部的热传导得到迅速补充,从而强化了翅片与空气的整体传热。根据上述分析可推论,翅片内部在长度及高度方向上的热传导在翅片强化传热过程中将起重要作用。为验证该推论,我们分别对翅片在厚度、长度及高度方向上的导热系数取较小值(1 W ·m-1 ·K-1),模拟计算电池及翅片的温度分布,结果如图 6及图 7所示,其中 a)为λthickness=λlength=λheight,b)为λthickness=1 W ·m-1 · K-1,c)为λlength=1 W ·m-1 ·K-1,d)为λheight=1 W ·m-1 ·K-1(放电倍率7 C,翅片厚度0.5 mm)。
|
| 图 6 翅片厚度、长度、高度方向导热系数分别取极小值和实际值时电池放电终止时电池的温度分布图 Figure 6 Impact of fin’s thermal conductivity of each direction on the heat dissipation using the fin-air cooling method |
| |
|
| 图 7 翅片厚度、长度、高度方向导热系数分别取极小值和实际值时翅片表面的表面温度分布图 Figure 7 Impact of fin’s thermal conductivity of each direction on temperature of fins using fin-air cooling method |
| |
由图 6可知,分别限制了热量在翅片厚度、长度及高度方向的热传导后,电池的温度均有所提高,但提高幅度差别巨大。相比之下,限制翅片厚度方向的热传导对电池散热影响较小,这是由于翅片较薄,厚度方向导热系数变小也无法明显影响该方向的热量传递。限制翅片长度与高度方向的热传导对电池散热影响较大,这一结果与上述推论一致。远离电池表面的空气温度较低,与相应位置翅片间的传热较快,所以限制了翅片长度方向的热传导后,该处翅片上被带走的热量无法得到快速补充,导致翅片表面沿长度方向出现明显的温度梯度[见图 7c)];翅片沿高度方向亦然[见图 7d)]。因此,翅片的作用除增大传热面积外,还在于能够迅速地将热量补充至传热较快的位置,使流道中温度较低的空气获得充分利用。这一机理也可用于解释翅片-空气协同冷却方法能够提高电池内部温度均匀性的现象。
根据上述分析,若需进一步强化翅片传热的能力,则除了增大翅片的表面积外,还可通过其它方法增强翅片在长度及高度方向的热传导能力。其中后者可通过两种方法实现:1)增大翅片厚度;2)增大翅片的导热系数。图 8给出了翅片厚度对放电终止时电池温升的影响,可知翅片厚度越大,翅片-空气协同冷却方法的控温效果越明显。这是由于增大翅片厚度能够增大翅片内部沿长度及高度方向热传导的截面积,从而强化传热。但是翅片厚度增大意味着电池间距变大、翅片质量增加,会导致电池组体积与重量增加,因此在电池组热管理系统设计时应予以权衡。表 3给出了翅片采用不同材料时电池的温升情况,可知翅片材料的导热系数对翅片-空气协同冷却方法的控温效果有重要影响。这是由于导热系数越大,翅片沿长度、高度方向及厚度方向的热阻就越小,控温效果就越好。

|
| 图 8 不同翅片厚度下电池放电终止时电池的最大温度图(放电倍率7 C,翅片材质为铝材) Figure 8 The maximum temperature of battery at discharge end with different thickness of fins(the discharge rate is 7 C,the material of fin is aluminum) |
| |
| 导热系数/(W·m-1·K-1) | Tmax/(℃) | |
| 铜 | 400.00 | 38.3 |
| 铝 | 160.00 | 44.9 |
| 铁 | 76.20 | 50.1 |
| 铅 | 35.30 | 54.7 |
| 塑料 | 0.18 | 62.7 |
| 无翅片 | 62.8 |
为有效抑制锂离子电池组在大倍率放电过程中的温升,提出了一种新的热管理方法,即翅片-空气协同冷却法。通过数值模拟检验了该方法的控温效果。结果表明,与传统空气冷却方法相比,翅片-空气协同冷却法不仅能有效降低电池的最大温度,提高单电池内部温度分布的均匀性,还在很大程度上降低了空冷散热的能耗。电池的放电倍率越大,翅片-空气协同冷却的控温效果就越明显。对翅片强化传热机理的分析表明,除增大传热面积外,翅片还能够通过内部热传导强化与流道中温度较低空气的传热,从而有效抑制了电池的温升。根据该机理,增大翅片厚度及选择导热系数大的材料均能提高翅片-空气协同冷却法的控温效果。此冷却方法简单易行,具有较大的潜在实用价值。
| [1] | Kizilel R, Sabbah R, Selman J R, et al. An alternative cooling system to enhance the safety of Li-ion battery packs[J]. Journal of Power Sources,2009,194 (2) : 1105–1112 |
| [2] | Kruger I, Sievers M, Schmitz G. Thermal modeling of automotive lithium ion cells using the finite elements method in modelica[C]//Proceedings 7th Modelica Conference, Italy, 2009, 43: 1-8 |
| [3] | Park H. A design of air flow configuration for cooling lithium ion battery in hybrid electric vehicles[J]. Journal of Power Sources,2013 : 30–36 |
| [4] | Paul N, Dennis D, Khalil A, et al. Modeling thermal management of lithium-ion PNGV batteries[J]. Journal of Power Sources,2002 : 349–356 |
| [5] | Mao S, Liu K, Yung Y W, et al. Heat dissipation design for lithium-ion batteries[J]. Journal of Power Sources,2002 : 160–166 |
| [6] | Rao Z, Wang S. A review of power battery thermal energy management[J]. Renewable and Sustainable Energy Reviews,2011,15 (9) : 4554–4571 |
| [7] | Cheng L, Ke C, Fengchun S, et al. Research on thermo-physical properties identification and thermal analysis of EV Li-ion battery[C]//Vehicle power and propulsion conference, VPPC'09, IEEE, 2009: 1 643-1 648 |
| [8] | Teng H, Ma Y, Yeow K, et al. Thermal characterization of a Li-ion battery module cooled through aluminum heat-sink plates[J]. SAE International,2011,4 (3) : 1311–1342 |
| [9] | 朱晓彤. RAV-4电动汽车电池组风冷系统的研究[D]. 南京: 南京航空航天大学,2007 |
| [10] | Zhu C, Li X, Song L, et al. Development of a theoretically based thermal model for lithium ion battery pack[J]. Journal of Power Sources,2013 : 155–164 |
| [11] | Xun J, Liu R, Jiao K. Numerical and analytical modeling of lithium ion battery thermal behaviors with different cooling designs[J]. Journal of Power Sources,2013 : 47–61 |
| [12] | Chen Y, Evans J W. Thermal analysis of lithium polymer electrolyte batteries by a twodimensional model-Thermal behaviour and design optimization[J]. Electrochimica Acta,1994,39 (4) : 517–526 |
 2016, Vol. 33
2016, Vol. 33





