
2. 中国电子科技集团第十八研究所, 天津 300381
2. Tianjin Institute of Power Sources, Tianjin 300381, China
直接甲醇燃料电池(DMFC)结构简单,安全性能高,持续供电时间长,能量密度高,对环境友好,可以作为飞机、火车、汽车以及便携式电子产品的理想电源[1]。但经过近20 a的研究,DMFC的阴极水淹、甲醇渗透、成本高等问题依然阻碍着DMFC的商业化。
直接甲醇液流燃料电池(DMRFC)使用液流电池电极代替传统的DMFC阴极电极,DMRFC的阴极只使用了一层电极,没有催化层和扩散层,而且反应液为氧化还原电对。Ilicic等[2]构筑的直接液流燃料电池(DLRFC)使用甲醇、甲酸等做阳极燃料,Fe3+/Fe2+为阴极氧化剂。DLRFC阴极和阳极均为液体进料,避免了阴极的水淹问题,阳极燃料渗透到阴极不会反应,避免了燃料渗透问题,阴极不需要使用贵金属催化剂,降低了电池的成本。
目前关于DMRFC的模拟研究还很少,Singh等[3]建立了一个电池结构和DMRFC一样的质子交换膜液流燃料电池模型,其阳极使用氢气为燃料,阴极使用5价钒和4价钒的氧酸盐作为氧化还原电对。但该模型只考虑了复杂的阴极过程,而没有考虑阳极电化学反应和物质传输。
本研究将建立1个二维两相等温的DMRFC单电池模型,该模型考虑了电池阳极和阴极所有层中的传输现象,以及二氧化碳气体的产生和甲醇通过质子交换膜的渗透,并通过该模型研究了阳极扩散层厚度,阳极催化层厚度和阴极Fe3+浓度对电池性能的影响。
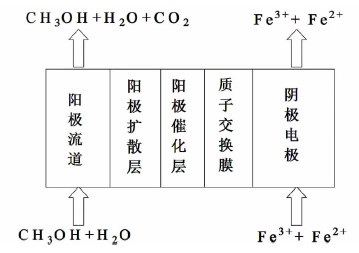
1 模型 1.1 模型的建立DMRFC的工作原理如图 1所示,模拟区域包括阳极流道(AFC)、阳极扩散层(ADL)、阳极催化层(ACL)、质子交换膜(PEM)和阴极电极(CE)。甲醇溶液沿流道通过阳极扩散层到达阳极催化层发生氧化反应,Fe3+在阴极电极处被还原为Fe2+,该电池的反应方程式可表述为:
|
| 图 1 DMRFC工作原理示意图 Fig. 1 The schematic diagram of DMRFC |
| |
阳极
| $${\rm{C}}{{\rm{H}}_3}{\rm{OH}} + {{\rm{H}}_2}{\rm{O}} \to {\rm{C}}{{\rm{O}}_2} + 6{{\rm{H}}^ + } + 6{{\rm{e}}^ - }$$ | (1) |
阴极
| $$6{\rm{F}}{{\rm{e}}^{3 + }} + 6{{\rm{e}}^ - } \to 6{{\rm{e}}^{2 + }}$$ | (2) |
总反应如式(3)。
| $${\rm{C}}{{\rm{H}}_3}{\rm{OH}} + {{\rm{H}}_2}{\rm{O}} + 6{{\rm{e}}^{2 + }} \to {\rm{C}}{{\rm{O}}_2} + 6{{\rm{H}}^ + } + 6{{\rm{e}}^{2 + }}$$ | (3) |
在本模型中使用如下假设:1)电池工作在恒温稳定的状态;2)流体为不可压缩的层流流动;3)扩散层、扩散层、质子交换膜、阴极电极为均质的和各向同性的多孔介质;4)产生的CO2气体不溶于甲醇水溶液;5)质子交换膜为水饱和;6)忽略集流板和阴阳极间的接触电阻;7)重力效应忽略不计。
1.1.1 物质传输方程甲醇在AFC和ADL中的传输方程如式(4)。
| $$\nabla \cdot \left( { - s_1^{1.5}D_{{\rm{MEOH}}}^{{\rm{eff}}}\nabla {C_{{\rm{MEOH}}}}} \right) + {u_1} \cdot {C_{{\rm{MEOH}}}} = 0$$ | (4) |
DMEOHeff为甲醇的有效扩散速率,ul为甲醇的流速,CMEOH为甲醇的摩尔浓度,sl为液体饱和度,由式(5)表示。
| $${s_1} = \frac{{{\rho _g}\left( {{C_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} - C_{{\rm{C}}{{\rm{O}}_{2,{\rm{g}}}}}^{{\rm{sat}}}} \right)}}{{{\rho _1}\left( {C_{{\rm{C}}{{\rm{O}}_{2,1}}}^{{\rm{sat}}} - {C_{{\rm{C}}{{\rm{O}}_2}}}} \right) + {\rho _g}\left( {{C_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} - C_{{\rm{C}}{{\rm{O}}_{2,{\rm{g}}}}}^{{\rm{sat}}}} \right)}}$$ | (5) |
CsatCO2,g表示CO2气体在气相中的饱和浓度,CsatCO2,l表示CO2气体在液相中的饱和浓度,ρg和ρl为气相和液相密度。
所有的有效扩散系数需要进行Bruggeman修正如式(6)。
| $${D^{{\rm{eff}}}} = {\varepsilon ^{1.5}}D$$ | (6) |
ε为多孔介质孔隙率。
CO2气体在AFC和ADL的传输方程如式(7)。
| $$\nabla \cdot \left( { - s_{\rm{g}}^{1.5}D_{{\rm{C}}{{\rm{O}}_2}}^{{\rm{eff}}}\nabla {C_{{\rm{C}}{{\rm{O}}_2}}}} \right) + {u_{\rm{g}}} \cdot {C_{{\rm{C}}{{\rm{O}}_2}}} = 0$$ | (7) |
sg为二氧化碳气体饱和度,sg和sl之和为1。
甲醇在ACL中的物质传输方程如式(8)。
| $$\begin{array}{l} \nabla \cdot \left( { - D_{{\rm{MEOH}}}^{{\rm{eff}}}\nabla {C_{{\rm{MEOH}}}}} \right) + {u_1} \cdot \nabla {C_{{\rm{MEOH}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{ - {j_{\rm{a}}}}}{F}\left( {\frac{1}{6} + n_{\rm{d}}^{{\rm{MeOH}}}} \right) \end{array}$$ | (8) |
ja为阳极体积电流密度,ndMeOH为甲醇的电拖曳系数,如式(9)所示。
| $$n_{\rm{d}}^{{\rm{MeOH}}} \cong n_{\rm{d}}^{{{\rm{H}}_{\rm{2}}}{\rm{O}}}\frac{{{C_{{\rm{MeOH}}}}}}{{{C_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\left| {_{{\rm{ACL|PEM}}}} \right.$$ | (9) |
其中nH2Od表示水的拖曳系数。
CO2气体在ACL中的传输方程如式(10)。
| $$\nabla \cdot \left( { - D_{{\rm{ACL,C}}}^{{\rm{eff}}}\nabla {C_{{\rm{C}}{{\rm{O}}_2}}}} \right){u_{\rm{g}}} \cdot \nabla {C_{{\rm{C}}{{\rm{O}}_2}}} = \frac{{{j_{\rm{a}}}}}{{6F}}$$ | (10) |
甲醇和水会经过质子交换膜渗透到阴极电极,甲醇在质子交换膜中的物质传输方程如式(11)。
| $$\nabla \cdot \left( { - D_{{\rm{PEM}}}^{{\rm{eff}}}\nabla {C_{{\rm{MEOH}}}}} \right) = 0$$ | (11) |
渗透到阴极电极的甲醇不参加反应,其在阴极电极的物质传输方程如式(12)。
| $$\nabla \cdot \left( { - D_{{\rm{PEM}}}^{{\rm{eff}}}\nabla {C_{{\rm{MEOH}}}}} \right) = 0$$ | (12) |
Lcell表示电池的高度,U表示甲醇在阴极电极处的层流流速。
Fe3+和Fe2+在阴极电极中的物质传输使用修正过的Nernst-Planck方程来描述,其物质传输方程如式(13)。
| $$\nabla \cdot \left( { - D_i^{{\rm{eff}}}\nabla {C_i} - \frac{{{z_i}{C_i}D_i^{{\rm{eff}}}}}{{RT}}F\nabla {\emptyset _1}} \right) + u \cdot \nabla {C_i} = \frac{{ - {j_{\rm{c}}}}}{F}$$ | (13) |
zi表示物质i的化学价,∅l表示质子导体电势,i代表Fe3+和Fe2+。
1.1.2 连续性和动量守恒方程气液两相在AFC和ADL中的连续性方程如式(14)。
| $$\nabla \cdot \left( {{s_i}{\rho _i}{u_i}} \right) = 0$$ | (14) |
i代表气相或液相。
气液两相在ACL中的连续性方程如式(15)和(16)。
| $${\rho _1}\nabla \cdot {u_1} = \sum {\frac{{ - {j_{\rm{a}}}}}{{6F}}{M_k}} $$ | (15) |
| $${\rho _{\rm{g}}}\nabla \cdot {u_{\rm{g}}} = v{M_{{\rm{C}}{{\rm{O}}_2}}}$$ | (16) |
Mk为物质k的摩尔质量,k代表CH3OH和H2O。
阳极流道中的动量守恒方程如式(17)。
| $${s_1}{\rho _1}\left( {{u_1} \cdot \nabla } \right){u_1} = - \nabla {P_1} + \nabla \cdot \left( {{s_1}{u_1}\nabla {u_1}} \right) + {s_1}{\rho _1}g$$ | (17) |
在ADL和ACL中,毛细压强和液相饱和度的关系如式(18)。
| $${P_{\rm{c}}} = {P_{\rm{g}}} - {P_1} = \sigma \cos \theta {\left( {\varepsilon /K} \right)^{0.5}}J\left( {{s_1}} \right)$$ | (18) |
其中Pc为毛细压强,σ为表面张力系数,θ为接触角,J(sl)为Leverett函数,如式(19)所示。
| $$J\left( {{s_1}} \right) = 1.417{s_1} - 2.12s_1^2 + 1.26s_1^3$$ | (19) |
使用Darcy定律来描述气液两相的动量守恒方程。
| $${u_i} = - K\frac{{{k_{{\rm{r}}i}}}}{{{\mu _i}}}\nabla {P_i}$$ | (20) |
K表示多孔介质的绝对渗透率,kri表示相对渗透率,μi表示动力学黏度,Pi表示压强。
| $${k_{{\rm{r}}i}} = s_i^3$$ | (21) |
阴极电极使用Darcy定律为动量守恒方程。
| $$\frac{\mu }{K}u = - \nabla P$$ | (22) |
其中阴极电极的渗透率如式(23)所示[4]。
| $$K = \frac{{d_{\rm{f}}^2{\varepsilon ^3}}}{{16{k_{{\rm{CK}}}}{{\left( {1 - \varepsilon } \right)}^2}}}$$ | (23) |
kCK表示Carman-Kozeny常数,df表示阴极电极纤维直径。
1.1.3 质子和电子守恒方程根据欧姆定律可以得到模型在不同区域的质子电流密度和电子电流密度,如方程(24)和(25)所示。
| $${i_1} = - {\sigma _1}\nabla {\emptyset _1}\left( {{\rm{ACL,PEM,CE}}} \right)$$ | (24) |
| $${i_{\rm{s}}} = - {\sigma _{\rm{s}}}\nabla {\emptyset _{\rm{s}}}\left( {{\rm{ADL,ACL,CE}}} \right)$$ | (25) |
il表示质子电流密度,is表示电子电流密度,σl为质子电导率,σs为电子电导率,∅l为电解质电势,∅s为电子导体电势。
阳极扩散层和质子交换膜中的电荷守恒方程如式(26)和(27)。
| $$\nabla {i_{\rm{s}}} = 0\left( {{\rm{ADL}}} \right)$$ | (26) |
| $$\nabla {i_1} = 0\left( {{\rm{PEM}}} \right)$$ | (27) |
在阳极催化层(ACL),电荷守恒方程如式(28)和(29)。
| $$\nabla {i_1} = {j_{\rm{a}}}$$ | (28) |
| $$\nabla {i_{\rm{s}}} = - {j_{\rm{a}}}$$ | (29) |
在阴极电极(CE),电荷守恒方程如式(30)和(31)。
| $$\nabla {i_1} = {j_{\rm{c}}}$$ | (30) |
| $$\nabla {i_{\rm{s}}} = {j_{\rm{c}}}$$ | (31) |
甲醇氧化产生的阳极体积电流密度用方程(32)表示[5],阳极过电势如式(33)。
| $${j_a} = \frac{{\alpha i_{{\rm{oa}}}^{{\rm{ref}}}{S_1}{C_{{\rm{MeOH}}}}\exp \left( {\left( {{\alpha _{\rm{a}}}F/RT} \right){\eta _{\rm{a}}}} \right)}}{{{C_{{\rm{MeOH}}}} + {k_{{\rm{MEOH}}}}\exp \left( {\left( {{\alpha _{\rm{a}}}F/RT} \right){\eta _{\rm{a}}}} \right)}}$$ | (32) |
ioaref表示参考交换电流密度,αa表示阳极催化层中的电荷传输系数,α表示阳极催化层的有效比表面积,kMEOH为甲醇的氧化反应速率,EaEq为阳极平衡电极电势。
阴极的电化学反应使用Butler-Volmer方程表示,阴极的体积电流密度如式(34)[6]。
| $${j_{\rm{c}}} = j_{\rm{c}}^0\left[ {\exp \left( {\frac{{{\alpha _{{\rm{c}}1}}{F_{{\eta _{\rm{c}}}}}}}{{RT}}} \right) - \exp \left( { - \frac{{{\alpha _{{\rm{c2}}}}{F_{{\eta _{\rm{c}}}}}}}{{RT}}} \right)} \right]$$ | (34) |
| $$i_{\rm{c}}^0 = Fk{\left( {{C_{2{\rm{s}}}}} \right)^{{\alpha _{{\rm{c}}1}}}}{\left( {{C_{3{\rm{s}}}}} \right)^{{\alpha _{{\rm{c2}}}}}}$$ | (35) |
| $${\eta _{\rm{c}}} = {\phi _{\rm{s}}} - {\emptyset _1} - E_{\rm{c}}^{{\rm{Eq}}}$$ | (36) |
C2s和C3s分别表示Fe2+和Fe3+在石墨毡反应处参加反应的实际表面浓度,αc1和αc2分别表示氧化和还原的电荷传输系数,ic0表示阴极的交换电流密度,k表示阴极标准反应速率常数。
1.2 边界条件甲醇在阳极入口处的浓度为已知,水在阳极入口处的浓度可由式(37)求得,阴极入口处的Fe3+和Fe2+浓度为已知。
| $${C_{{{\rm{H}}_{\rm{2}}}{\rm{O,in}}}} = \frac{{{\rho _{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}{{{M_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}} \times \left( {1 - \frac{{{C_{{\rm{MEOH,in}}}}{M_{{\rm{MEOH}}}}}}{{{\rho _{{\rm{MEOH}}}}}} - \frac{{{C_{{\rm{H}}_{{\rm{in}}}^ + }}{M_{{{\rm{H}}^ + }}}}}{{{\rho _{{{\rm{H}}^ + }}}}}} \right)$$ | (37) |
阳极流道和阳极扩散层交界面的电势为零,如式(38),阴极和阴极集流体(CC)的交界面电势为电池电压,如式(39)。
| $${\emptyset _{{\rm{s,AFC/ADL}}}} = 0$$ | (38) |
| $${\emptyset _{{\rm{s,CE/CC}}}} = {V_{{\rm{cell}}}}$$ | (39) |
电池出口处边界条件如式(40),电池内部边界为连续性边界条件,其余边界条件为电绝缘和无滑移边界条件。
| $$ - n \cdot {D_i}\nabla {C_i} = 0$$ | (40) |
平均电流密度通过对阳极催化层中电流密度的积分表示,如式(41)所示。
| $${{i}_{\text{cell}}}=\frac{1}{{{L}_{\text{cell}}}}\iint{{{i}_{\text{a}}}\text{d}x\text{d}{{y}_{\text{ACL}}}}$$ | (41) |
电池的功率密度使用式(42)计算。
| $${W_{{\rm{cell}}}} = {i_{{\rm{cell}}}}{V_{{\rm{cell}}}}$$ | (42) |
通过有限元方法离散化模型中所使用的方程,并使用商业化软件Comsol Multiphysics4.2a求解,模型所需要的基本参数如表 1所示。
| 参数 | 数值 |
| 阳极扩散层孔隙率εADL | 0.6[7] |
| 阳极催化层孔隙率εACL | 0.4[7] |
| 质子交换膜孔隙率εPEM | 0.28[7] |
| 阴极电极孔隙率εCE | 0.68 |
| 碳电极平均孔直径df | 1.7×10-5 m[8] |
| 阳极扩散层电导率σADL | 300 S·m-1 |
| 质子交换膜电导率σPEM | 10.98×${\rm{e}}\left( {1268\left[ {\frac{1}{{303}} - \frac{1}{T}} \right]} \right)$S·m-1 |
| 阴极电极电导率σCE | 500 S·m-1 |
| 甲醇在水中的扩散系DMEOH | 2.8×10-9${\rm{e}}\left( {\frac{{2436}}{{353}} - \frac{{2436}}{T}} \right)$ m2·s-1[9] |
| 甲醇在膜中的扩散系数DMEOH,PEM | 4.9×10-10${\rm{e}}\left( {\frac{{2436}}{{353}} - \frac{{2436}}{T}} \right)$ m2·s-1[9] |
| Fe3+的扩散系数(296 K)DFe3+ | 3.32×10-10 m2·s-1[10] |
| Fe2+的扩散系数(296 K)DFe2+ | 3.95×10-10 m2·s-1[10] |
| CO2气体的扩散速率DCO2 | 3.0×10-5×${\left( {\frac{T}{{353.15}}} \right)^{1.5}}$ m2·s-1[11] |
| 气体的黏度μg | 2.03×10-5 kg·m-1·s-1[12] |
| 液体黏度μl | 4.05×10-4 kg·m-1·s-1[12] |
| Kozeny-Carman常数kCK | 4.28[9] |
| 阴极反应速率常数k | 1.6×10-5${\rm{e}}\left( {\frac{{{\rm{FE}}_{\rm{c}}^0}}{R}\left[ {\frac{1}{{{T^{{\rm{ref}}}}}} - \frac{1}{T}} \right]} \right)$ m·s-1[6] |
| 阳极参考交换电流密度ioaert | 94.25×${\rm{e}}\left( {\frac{{35571}}{R}\left[ {\frac{1}{{353}} - \frac{1}{T}} \right]} \right)$ A·m-2[13] |
| 甲醇氧化反应速率kMEOH | 2.265×10-3 mol·m-3[5] |
| 水的电拖曳系数nd | 2.9×${\rm{e}}\left( {\frac{{1029}}{{333}} - \frac{{1029}}{T}} \right)$ |
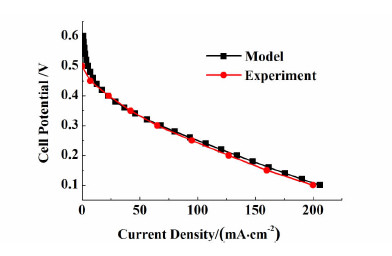
为了验证模型的准确性,将模拟结果同Llicic[2]的实验结果对比。从图 2中可以看出模拟结果同实验结果很好的吻合。电池的工作温度为70 ℃,阴极溶液组成为0.81 mol·L-1 NH4Fe(SO4)2+0.09 mol·L-1FeSO4+0.5 mol·L-1 H2SO4混合溶液,阳极溶液组成为2 mol·L-1 CH3OH+0.5 mol·L-1 H2SO4混合溶液,阴阳极流体流量都为5 mL·min-1。
|
| 图 2 DMRFC两相模型的验证 Fig. 2 The validation of DMRFC two-phase model |
| |
不同扩散层厚度对电池性能的影响如图 3所示。

|
| 图 3 阳极扩散层厚度对电池性能的影响 Fig. 3 The influence of ADL thickness on cell performance |
| |
从图 3中可以看出,随着阳极扩散层厚度的增加,电池的性能降低。当扩散层厚度从2×10-5 m增加到6×10-4 m时,电池的最大电池功率从32.18 mW·cm-2减少到了24.35 mW·cm-2,极限电流密度从253.93 mA·cm-2减少到184.65 mA·cm-2,当扩散层厚度为0 m即没有扩散层时,电池的功率密度和极限电流密度为最大,达到34.30 mW·cm-2和273.7 mA·cm-2。这是由于随着阳极扩散层厚度的增加,甲醇水溶液向阳极催化层扩散需要经过更长的距离,不利于甲醇水溶液在扩散层中的对流扩散传输,而且随着扩散层厚度的增加,扩散层的电阻也会不断增加,加大了电池的欧姆阻抗,从而降低了电池性能。从理论上分析,越薄的扩散层有利于甲醇快速传输到催化层参加反应,能够显著减少传质阻力,越有利于提高电池性能,但太薄的扩散层机械强度过低,不利于对催化层的支撑,容易导致催化剂的脱落,因此要根据实际情况来选择合适的扩散层厚度。
2.3 阳极催化层厚度的影响阳极催化层是甲醇参加电化学反应的场所,不同催化层厚度对电池性能的影响如图 4所示。

|
| 图 4 阳极催化层厚度对电池性能的影响 Fig. 4 The influence of ACL thickness on cell performance |
| |
当催化层厚度为3×10-5 m,催化剂PtRu/C[40%,n(Pt)/n(Ru)=1]载量为2 mg·cm-2,催化剂在催化层中均匀分布,即同一催化层截面催化剂含量相同,催化剂含量和催化层厚度成正比。催化层厚度为10-5 m时,由于催化层太薄而没有为反应提供足够的催化剂,导致催化层中电化学反应的动力学过程十分缓慢,从而降低了电池的性能。当催化层厚度不断增加时,电池的性能不断提高,这是由于随着催化层厚度的提高,催化剂的载量也跟着增高,为甲醇参加电化学反应提供了更多的活性位,提高了电池电化学反应的动力学性能。从图 4中还可以看出,当催化层厚度大于5×10-5 m时,电池性能随着催化层厚度的增加并没有显著提高,这是由于增加催化层的厚度,增大了甲醇水溶液的传质阻力和电池的欧姆阻抗,抵消了催化活性增强的影响,电池性能的提高将变得缓慢。因此在选择催化层厚度时,催化层太薄不利于提供足够的催化剂,而降低电池性能,催化层太厚则会增加成本、传质阻力和欧姆阻抗,因此在设计电池时要综合考虑各方面的影响来确定催化层厚度。
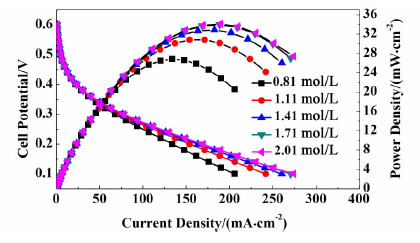
2.4 Fe3+浓度的影响不同Fe3+浓度对电池电压和功率密度的影响如图 5所示。
|
| 图 5 Fe3+浓度对电池性能的影响 Fig. 5 The influence of Fe3+ concentration on cell performance |
| |
从图 5中可以看出,在低电流密度区域,增加Fe3+浓度对电池性能影响很小,这是由于在低电流密度区域,Fe3+的消耗少,0.63 mol·L-1的Fe3+已经足够满足电化学反应的需求,当继续增加Fe3+浓度时,会形成富足的Fe3+浓度,多余的Fe3+并没有参加反应,所以对电池的性能影响不大。在高电流密度区域,增大Fe3+浓度会显著提高电池的性能,高的Fe3+浓度会使电池拥有高的极限电流密度,这是由于在高电流密度下,Fe3+的消耗过多,增加Fe3+浓度将会满足阴极电化学反应对Fe3+的需求。当Fe3+浓度从0.81 mol·L-1增加到1.41 mol·L-1时,电池的最大功率密度由26.83 mW·cm-2增加到了32.87 mW·cm-2,电池性能显著提高。但当Fe3+浓度大于1.41 mol·L-1时,增加Fe3+浓度并没有提高电池性能,这是由于电池的性能是受阴阳极氧化还原电位共同决定的,在阳极电位不变情况下,单纯的增加阴极反应物浓度并非总能提高阴极氧化还原电位。
3 结论建立了一个DMRFC二维两相模型,并和实验数据对比,发现模拟的极化曲线和实验结果吻合很好,验证了模型的正确性,利用该模型得到以下结论。
1)减小阳极扩散层的厚度有利于减少物质传输阻力和电池的欧姆阻抗,从而可以增加电池的性能,但是扩散层太薄的机械强度不利于支撑催化层,降低了电池的结构稳定性,所以应该根据实际需要,综合考虑选择合适的扩散层厚度。
2)增大阳极催化层的厚度,提高了催化剂的含量,能够显著提高电池的性能,但当催化层厚度大于5×10-5 m时,物质传输阻力和电池欧姆阻抗的增大会抵消催化剂含量增加的影响,同时电池成本也会增加,因此应该选择厚度适中的催化层厚度。
3)提高阴极电极入口的Fe3+浓度,能够给阴极反应提供更多的反应物质,提高阴极反应的动力学性能,提高电池性能,但当Fe3+浓度高于1.41 mol·L-1时,浓度的增加并不能提高电池性能。
| [1] | Kamarudin S K, Achmad F, Daud W R W. Overview on the application of direct methanol fuel cell (DMFC) for portable electronic devices[J]. International Journal of Hydrogen Energy,2009,34 (16) : 6 902–6 916 |
| [2] | Ilicic A B, Dara M S, Wilkinson D P, et al. Improved performance of the direct methanol redox fuel cell[J]. Journal of Applied Electrochemistry,2010,40 (12) : 2 125–2 133 |
| [3] | Singh R, Shah A A, Potter A, et al. Performance and analysis of a novel polymer electrolyte membrane fuel cell using a solution based redox mediator[J]. Journal of Power Sources,2012 : 159–163 |
| [4] | Tomadakis M M. Viscous permeability of random fiber structures:Comparison of electrical and diffusional estimates with experimental and analytical results[J]. Journal of Composite Materials,2005,39 (2) : 163–188 |
| [5] | Meyers J P, Newman J. Simulation of the direct methanol fuel cell[J]. Journal of the Electrochemical Society,2002,149 (6) : A718–A728 |
| [6] | Shah A A, Tangirala R, Singh R, et al. A Dynamic unit cell model for the all-vanadium flow battery[J]. Journal of The Electrochemical Society,2011,158 (6) : A671–A677 |
| [7] | Ge J, Liu H. A three-dimensional mathematical model for liquid-fed direct methanol fuel cells[J]. Journal of Power Sources,2006,160 (1) : 413–421 |
| [8] | Zhou H, Zhang H, Zhao P, et al. A comparative study of carbon felt and activated carbon based electrodes for sodium polysulfide/bromine redox flow battery[J]. Electrochimica Acta,2006,51 (28) : 6 304–6 312 |
| [9] | Colpan C O, Fung A, Hamdullahpur F. 2D modeling of a flowing-electrolyte direct methanol fuel cell[J]. Journal of Power Sources,2012 : 301–311 |
| [10] | Stephenson D, Kim S, Chen F, et al. Electrochemical model of the Fe/V redox flow battery[J]. Journal of the Electrochemical Society,2012,159 (12) : A1 993–A2 000 |
| [11] | Wang Z, Wang C. Mathematical modeling of liquid-feed direct methanol fuel cells[J]. Journal of the Electrochemical Society,2003,150 (4) : A508–A519 |
| [12] | Yang W, Zhao T. A two-dimensional, two-phase mass transport model for liquid-feed DMFCs[J]. Electrochimica Acta,2007,52 (20) : 6 125–6 140 |
| [13] | Yang W, Zhao T. Two-Phase, mass-transport model for direct methanol fuel cells with effect of non-equilibrium evaporation and condensation[J]. Journal of Power Sources,2007,174 (1) : 136–147 |
 2016, Vol. 33
2016, Vol. 33






