目前,我国钻井液的固相控制主要特点是浅地层需要处理的钻井液流量大;深地层需要处理的钻井液流量小,黏度高,并且随着钻井工艺水平的不断提高,传统钻井振动筛已不能满足实际的工程需要。
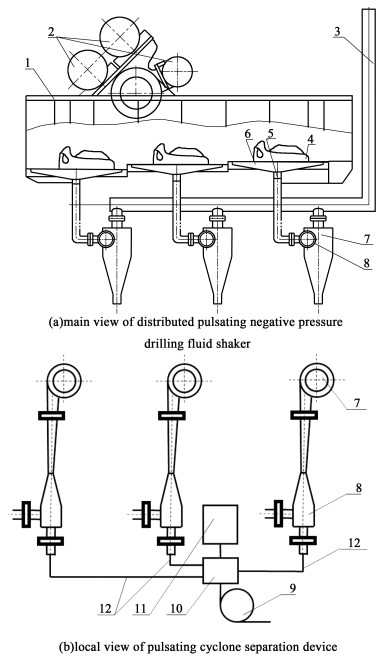
挪威CUBILITY AS公司发明了Mud Cube固相控制系统[1],利用带式真空过滤与高频微振的复合作用实现固液分离,可以将排出钻屑的含液率从传统振动筛的80%以上降低到40%以下,筛网下气液混合物,通过重力分离实现气液分离,通过二级过滤实现油雾分离,但该系统成本高,易损件寿命短,功耗大。丹尼尔·盖·波默洛[2]提出了在传统钻井液振动筛的筛网下部复合真空作用,强化振动筛的固液分离能力,大幅降低排出钻屑的含液量,并通过重力分离原理实现气液分离,但其真空大小受振动筛的振动参数限制,不能太大,因此难以充分发挥真空对钻屑的干燥作用。侯勇俊等[3-5]提出的脉动负压振动设备如图 1,通过压缩空气脉动喷射在筛面下产生脉冲负压,可充分发挥负压对钻屑的干燥作用;喷射泵排出的气液混合物通过旋流器实现气液分离,很显然,进入旋流器的气液混合物压力是脉动的,旋流器的气液分离性能及变化规律需要深入研究。
|
| 1-Screen frame; 2-Vibrating motor; 3-Gas discharge pipe; 4-Screen; 5-Flexible pipe; 6-Mud plate; 7-Gas-liquid cyclone separator; 8-Injection pump; 9-Air compressor; 10-High pressure air distributor; 11-Distribution motor; 12-High pressure air distribution line 图 1 脉动进料旋流分离器局部视图 Fig.1 Local view of the pulsating feed cyclone separator |
| |
杨兆铭等[6]设计了一种二级旋流气液分离装置,通过CFD和试验结合的方法对简化的分离装置内部流场的非对称性进行分析,发现入口面积和升气管的大小会影响旋流流场的稳定性。左鹏等[7]针对一种多旋臂的气液旋流分离器利用CFD模拟的方式选取RSM模型对其进行气相的流场特性分析,得到了和实验值较为符合的压力降分布。刘彩玉等[8]通过CFD仿真模拟对一种同向出流气液分离器进行了流场分析,通过性能规律曲线进行了参数优选,并制作了试验模型进行了验证。韩国的Chu等[9]通过CFD和CFD-DEM双向耦合的方式对自然旋流介质旋流器(NMC)进行了分析,将模拟结果与物理实验结果进行了比较,并对2种重要的操作参数,即介质速度和质量比在NMC入口的影响进行了数值研究。Liu和Yan等[10]使用Fluent仿真软件对井下油水旋流分离器进行分析,研究了几何因素对分离效率和分流比的影响,优化了几何结构,发现在下锥角在大于0.5°,小于3.0°时,可获得合适的分流比和高效率。
上述研究中,不论是气液分离还是固液分离都是采用稳定进料的边界条件进行模拟分析,均未曾研究过脉动进料边界条件下分离器的分离性能及其影响参数。
1 数值模拟 1.1 流体控制方程工作流体在旋流分离中常常呈强烈三维旋流状态,各相之间呈各向异性,根据常见湍流模型分类及特点[11, 12],选择雷诺应力(RSM模型)作为数值模拟计算的湍流模型,其流体控制方程[13]如下。
(1) 连续性方程:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x_j}\left(\rho u_j\right)=0 $ | (1) |
式(1)中:速度uj为j方向上的分量,j表示空间坐标,j=1,2,3;ρ表示流体密度。
(2) 动量方程:
| $ \frac{\partial}{\partial t}\left(\rho u_i\right)+\frac{\partial}{\partial x_j}\left(\rho u_i u_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_j}\left(\tau_{i j}\right)+\rho \mathrm{g}_i+F_i $ | (2) |
式(2)中:uiuj表示速度在ij方向上的分量;p为静压;τij等于黏性应力张量;ρgi指i方向上的重力体积力;Fi表示i方向的外部体积力和其他用户自定义源项之和。
(3) 分离效率:旋流分离器中气液2项分离方程[14]可通过同一位置的钻井液、气体作圆周运动的离心力的大小来表示。
| $ F_{i=z, k}=\frac{K M v^2}{R} $ | (3) |
| $ v=2 {\rm{ \mathsf{ π}}} n R $ | (4) |
| $ M_{j=z, k}=\rho V g $ | (5) |
| $ \frac{{{F_z}}}{{{F_k}}} = \frac{{4K{M_z}{n^2}{{\rm{ \mathsf{ π} }}^2}R}}{{4K{M_k}{n^2}{{\rm{ \mathsf{ π} }}^2}R}} = \frac{{4K{\rho _z}Vg{n^2}{{\rm{ \mathsf{ π} }}^2}R}}{{4K{\rho _k}Vg{n^2}{{\rm{ \mathsf{ π} }}^2}R}} = \frac{{{\rho _z}}}{{{\rho _k}}} $ | (6) |
式(3)~式(6)中:Fi=z, k表示为钻井液或气体所受离心力,N;K表示质量修正系数,为无量纲常数;Mj=z, k表示钻井液或空气质量,kg·m-3;v表示钻井液或空气作圆周运动的线速度,m·s-1;R表示钻井液或空气作圆周运动的半径,m;n表示钻井液或空气作圆周运动的转数。根据式(6)知,工作流体的分离离心力大小与其密度有关,旋流分离器正是利用这一工作原理进行气液分离。
目前数值模拟中对于定义旋流分离器气液分离效率的方法较多,在Fluent中为表示旋流分离器的气液分离效率[15],定义气体溢流口质量流量与气体进口质量之比为该分离器的气液分离效率。
| $ E = \frac{{{Q_{\rm{o}}}}}{{{Q_{\rm{i}}}}} \times 100\% $ | (7) |
式(7)中;E表示气体分离效率,%;Qo表示气体溢流口质量流量,kg·s-1;Qi表示气体入口质量流量,kg·s-1。
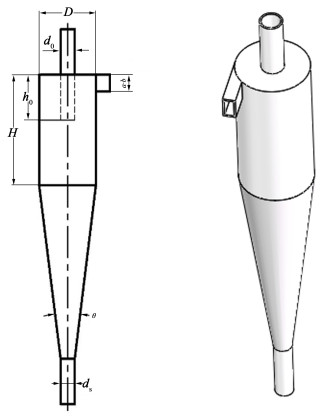
1.2 物理模型与边界参数 1.2.1 几何模型及参数基于里马特经验公式[16]得到旋流分离器的几何模型的结构参数,建立流体域,相关旋流结构如图 2所示,初始几何参数尺寸如表 1所示。
|
| 图 2 旋流分离器结构模型 Fig.2 Structural model of cyclone separator |
| |
| 项目 | 数值 |
| D/mm | 200 |
| a×b/mm2 | 60×35 |
| d0/mm | 68 |
| ds/mm | 50 |
| H/mm | 389 |
| h0/mm | 160 |
| θ/(°) | 14 |
选择CFD计算软件为Fluent,多相流模型为混合(mixture)模型,相数为2,设置的相关材料物理参数如表 2所示。
| 介质 | 密度/(kg·m-3) | 黏性/(Pa·s) | 比例 | 次序 |
| 高压空气 | 4.62 | 1.793×10-5 | 0.8 | 次要 |
| 钻井液 | 1600 | 1.095×10-3 | 0.2 | 主要 |
旋流分离器流体计算域采用以六面体结构网格为主的划分方式,为了保证在入口网格的平顺性和计算结果的精确性,对进口处的网格进行非结构化细化。为保证仿真结果的准确性和稳定性,采用上述相同的物理参数和边界条件对网格数量10万、22万、30万、50万和80万5种旋流分离器模型进行数值模拟,以旋流分离器气液分离效率为指标,对网格无关性验证后,最终确定选择网格数量为220 792个。
1.2.4 初值边界条件和计算格式在稳定进料条件下,设初始进料压力0.3 MPa,设置进口边界条件为速度入口,钻井液和空气进口速度均为24 m·s-1;溢流口和底流口均采用压力出口边界条件,设置出口压力为0;溢流口气体回流率为1,底流口气体回流率为0;壁面采用光滑无位移的边界;压力-速度场采用SIMPLEC算法,压力插值采用PRESTO格式,其余项均采用QUICK为主的二阶收敛格式。
2 2种状态下的变量控制 2.1 稳定进料条件下的变量稳定进料状态下,查阅相关参考文献[17, 18]可以得知其影响气液分离效率的因素主要包含2大类:模型本身的结构参数和介入待分离的流体参数(操作参数),为保证在本工况下的最佳气液分离效率,需对相关参数采取控制变量法进行参数优选得到最佳分离效率曲线下的相关参数,进行仿真计算时,为保证变量唯一性,除变量值发生改变外,其他未提及参数均按初始参数设置。结构和操作参数及其变量值如表 3和表 4所示。
| 序号 | 变量名称 | 变量值 |
| 1 | 溢流管深度/mm | 100、120、140、160 |
| 2 | 入口截面积a×b/mm2 | 40×30、50×35、60×30、60×35 |
| 3 | 锥角/(°) | 12、14、16 |
| 4 | 溢流口直径/mm | 50、56、62、68 |
| 序号 | 变量名称 | 变量值 |
| 1 | 钻井液密度/(kg·m-3) | 1 200、1 400、1 600、1 800、2 000 |
| 2 | 钻井液流速/(m·s-1) | 12、16、20、24、28 |
| 3 | 底流背压/Pa | 0、300、600、900、1200 |
| 4 | 空气体积分数 | 0.2、0.4、0.6、0.8 |
为实现脉动进料边界条件下对旋流分离器的
入口条件控制,需借助Fluent的用户自定义函数[19-22]即UDF进行编程编译,本研究使用的是Visual Studio 2015进行C文件的编程和储存。为得到在脉冲进料边界下的最佳分离效率,需要控制变量对脉冲函数类型、脉冲频率、脉冲速度峰值等影响参数进行优选。模拟工程状态下的脉冲,可以以Fluent中的UDF函数作为边界条件来代替实际工程中的配送器,如图 1所示。为探究脉冲条件下各个参数对分离效率的影响情况,本节将从脉冲类型、脉冲频率大小、脉冲速度峰值大小等3个主要参数进行控制变量,进行仿真计算时,为保证变量唯一性,除变量值发生改变外,其他未提及参数均按初始参数设置,部分UDF函数如下。
(1) 矩形脉冲函数:
if (t>=0&&t<=0.5) v=0;
else if (t>0.5&&t<=1) v=24。
(2) 三角形脉冲函数:
if (t>=0&&t<=0.5) v=48t;
else if (t>0.5&&t<=1) v=48-48t。
(3) 正弦波形脉冲函数:
v=12sin((0.8πt-π/2)+12。
在钻井工程实际生产中,常用脉冲频率一般为0.1~1.0 Hz,为实现脉动流体入口速度在0~24 m/s之间周期性来回切换,得到最佳分离效率下的脉冲频率,通过VS软件以C语言程序进行编译并加载到Fluent中进行边界条件控制,相关脉冲参数及其变量值如下表 5所示。
| 序号 | 变量名称 | 变量值 |
| 1 | 脉冲函数类型 | 矩形、三角形、正弦 |
| 2 | 脉冲频率/Hz | 0.2、0.4、0.6、0.8、1.0 |
| 3 | 峰值脉冲速度/(m·s-1) | 12、16、20、24 |
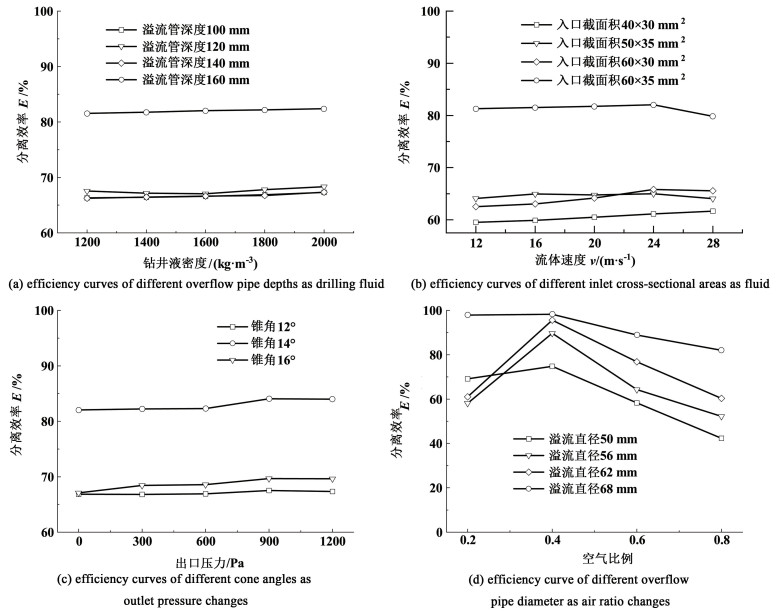
监测仿真计算结果中的气体进口质量流量和溢流出口的质量流量,通过式(7)进行计算得到气液分离效率,其效率曲线如图 3所示。
|
| 图 3 不同结构参数在不同操作参数下的效率曲线变化 Fig.3 The efficiency variation of different structure parameters with different operation parameters |
| |
从图 3(a)中横向对比发现随着钻井液密度的增加,整体分离效率略有波动,说明钻井液密度在小范围幅度变化时对气液分离效率影响很小,纵向对比中,溢流管深度在160 mm时气液分离效率最高,其他3者气液分离效率随参数变化时,气液分离效率稳定在67%附近。图 3(b)中4种不同入口截面积随着不同入口速度的变化,分离效率波动幅度较小,当入口截面积为60×35 mm2时其分离效率和其他3者差异较大。从图 3(c)中,横向对比发现在出口压力900 Pa时,3种结构下气液分离效率会略微提高;纵向对比中发现当锥角为14°时,气液分离效率比其他2种结构更高。从图 3(d)中横向对比发现压缩空气比重大小能较大地影响分离效率,体积分数在40%左右时,气液分离效率达到最高98.2%,纵向随着溢流直径的增加,整体分离效率有逐渐提高的趋势。
综上,当稳定进料旋流气液分离器的结构参数如溢流直径62 mm、溢流管深度160 mm、锥角14°、入口截面积60×35 mm2时,气液分离效率最高。当压缩气体占比0.4时,气液分离效率达到最高98.2%,操作参数中的进口速度、钻井液密度、背压等的改变使分离效率在小范围内有所波动,说明在一定程度上调节操作参数可使得气液分离效率提高。
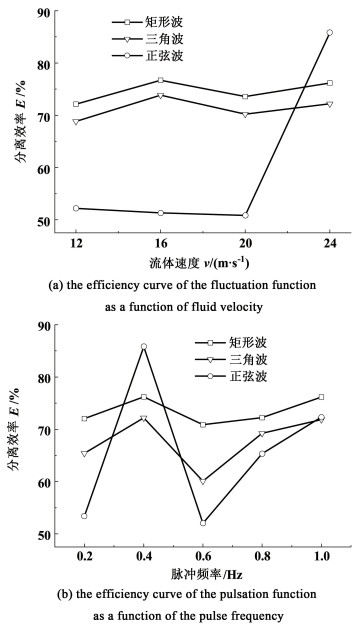
3.1.2 脉动进料效率曲线及参数优选以同样的方式将脉动进料条件下仿真得到的气体进口质量流量和溢流口质量流量,通过式(7)计算后可以得到关于3种函数在不同脉冲参数下的效率性能曲线图(图 4)。
|
| 图 4 不同脉冲参数下效率变化曲线 Fig.4 The efficiency variation curve under different pulse parameters |
| |
从图 4(a)可以看出,脉冲速度在12~20 m·s-1时,矩形脉冲波形下的气液分离效率是最高的,脉冲速度在20~24 m·s-1时,正弦波形脉冲下的气液分离效率最高;在图 4(b)中,3种脉冲波形在频率为0.4 Hz时气液分离效率都较其他更高。尤其是正弦波形,当脉冲频率为0.4 Hz,脉冲速度为24 m·s-1时,正弦脉冲的气液分离效率最高,达到85.5%。在一定程度上三角波和正弦波效率曲线走势接近,但工程实际控制中很难做到像矩形脉冲一样的速度陡降或陡升,三角波和正弦形波更为贴近实际工程。综上,选择正弦波作为分离函数来控制边界条件进行分离,最适宜分离频率为0.4 Hz,脉冲入料平均速度为24 m·s-1。
3.2 2种进料状态下的流场迹线及气相分布为进一步清晰地表示出脉动进料条件下的流场内部参数,如切向速度、径向压力、湍流动能等变化情况,对旋流分离器的内部流场进行探究和分析,得到了2种进料状态下的流场迹线云图(图 5)和气相体积分数分布云图(图 6)。
|
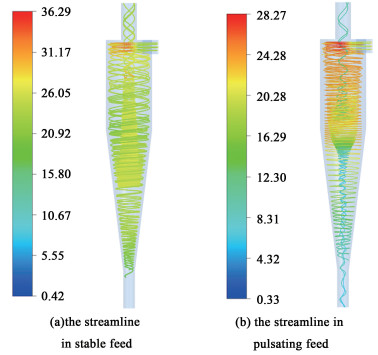
| 图 5 2种不同进口压力状态下的流场轨迹云图(m·s-1) Fig.5 The nephograms of streamline under two different inlet states(m·s-1) |
| |
|
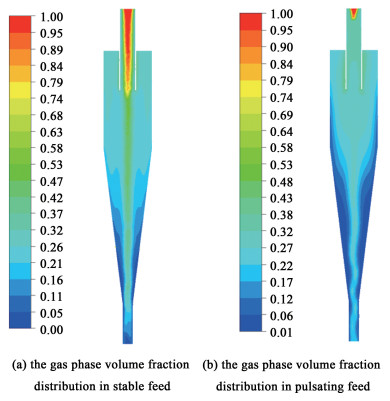
| 图 6 2种不同进口压力状态下的气相体积分数分布云图 Fig.6 The nephograms of gas phase volume fraction distribution under two different inlet states |
| |
从图 5中可以看出,2者速度峰值出现的位置相似,脉动进料条件下,速度峰值较稳定进料更低,从速度云图中可以发现,脉动进料条件下速度值从旋流器进口到底流口降低的幅度比稳定进料条件下低,速度下降得越慢,内部轴向压力降和压力损失越低。从旋流迹线上来看,2种进料状态下气液两相的轨迹线都比较明显,均未出现紊乱流线和逆流线,在脉动条件下,气液分离能形成较好的稳定性,旋流中部都形成了空气柱的轨迹线,值得注意的是,在空气柱的大小方面,稳定进料状态下的分离区域的空气柱较脉动进料状态下更大,这也是导致脉动进料下的气液分离效率较稳定进料状态下低一些的原因之一。
从图 6中可以看出,稳定进料状态的稳态计算状态下,气相体积分数多集中于溢流管附近,分离效果良好,旋流器混流区、旋流区和分离区壁面处气相几乎为0。脉动进料状态下,溢流管附近的气相体积分数略低于稳定进料状态,在旋流区和分离区附近还含有部分气相,说明在实际的脉动进料状态下进行气液分离的分离效率要低于稳定进料状态。从气相体积分数分布来看,2种进料状态都有沿Z轴近似左右对称分布的规律,内部主要气相分布位置较为相似,脉动进料条件下的分离区的气相分布稍有波动。
3.3 2种进料状态下流场参数变化情况 3.3.1 湍动能湍流动能和湍流耗散率都是表征流体运动稳定性的指标,湍流动能和湍流耗散率越大,流体运动越不稳定,越容易产生涡流。本研究以湍流动能为例,通过与稳定进料状态下同参数的旋流分离器内部流场进行比较,并截取3个主要运动界面:混流区(Mixed flow zone)、旋流区(Swirling zone)、分离区(Separation zone),如图 7所示,分析得到了如图 8所示的湍流动能变化情况示意图。

|
| 图 7 取点截面示意图 Fig.7 Schematic diagram of cross section of taking points |
| |
|
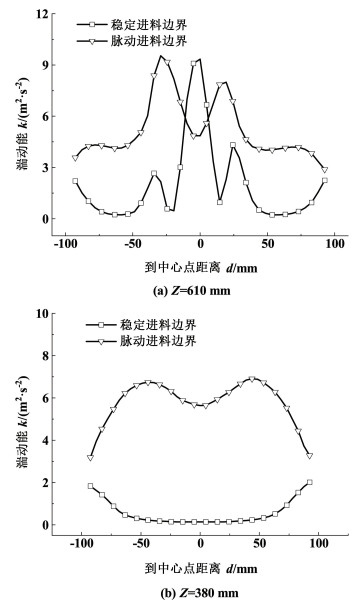
| 图 8 2种不同进料条件下分离器内部湍流动能变化 Fig.8 Variation of turbulent kinetic energy inside the separator under two different feeding conditions |
| |
从图 8的分析可以得到,脉动进料条件在进口(混流区Z=610 mm)截面、Z=380 mm的旋流区的平均湍流动能均高于稳定进料状态,脉动进料条件在此截面湍流动能变化无序,波动较大,流体性质不稳定,易产生涡流。在Z=0 mm时的分离区时,壁面处稳定进料条件下的湍流动能是高于脉动进料条件下的,其余地方的湍流动能均低于脉动进料条件下,说明脉动条件工作流体在壁面处稳定性更好,其他区域则是稳定进料条件下的稳定性更好。
3.3.2 径向压力降压力降是进行旋流分离器结构设计的重要考虑因素,在某一范围内,适当的压力降不仅让旋流分离器内部流体的运动更加稳定,还会极大地促进多相流之间的分离。本研究对在2种不同进料状态的旋流分离器内部的压力降分布情况进行对比,通过压力降的变化来预测流体运动的趋势和流体的稳定性。内部流场按压力作用方向可分为轴向压力降和径向压力降2种,以同一平面上即径向压力降为例,理论上径向压力梯度变化越大,越有利于两相的分离。
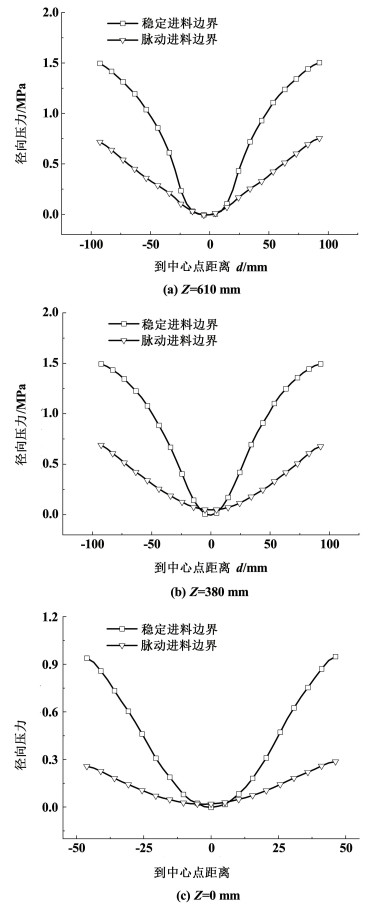
在图 9中横向对比来看稳定进料条件下从混流区从壁面到中心点径向压力平均值要大于脉动进料条件下同位置时的平均径向压力值,2种进料条件下点位越靠近中心点其径向压力值越低;2者的径向压力变化趋势都是关于Z轴近似左右对称的,这说明了运动的相对稳定性,均未出现紊乱流波动的情况。从旋流分离器的进口到底流口,即图 9(a)~图 9(c)的纵向对比来看,稳定进料条件下的压力梯度变化更大,这说明稳定进料下多相流的气液分离效率更高,更适合两相分离。
|
| 图 9 2种不同进料条件下分离器内部径向压力变化 Fig.9 Variation of radial pressure inside the separator under two different feeding conditions |
| |
旋流分离器内部速度矢量主要由3个方向上的分量组成,主要包括轴向速度、径向速度和切向速度3种,其中对分离效率影响最大的是切向速度。
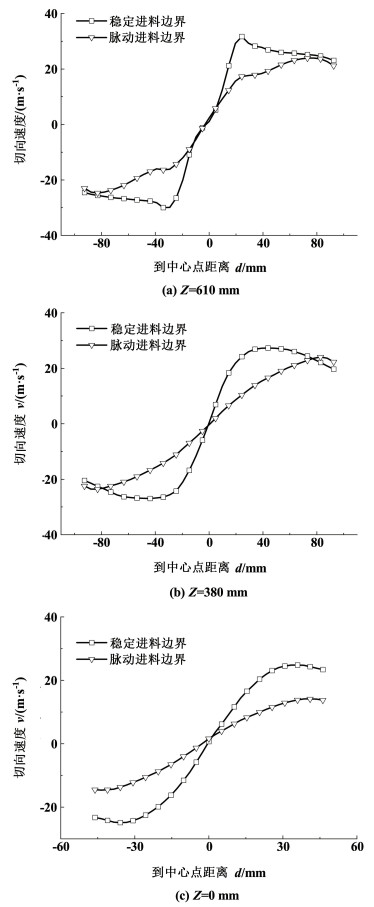
从图 10的2种不同进料工况的切向速度的分析中可知,在Z=380 mm的壁面处,脉动进料的切向速度值是大于稳定进料条件下的切向速度值,此时脉动进料下的速度流场更适合进行气液分离,而在Z=0 mm出口截面和Z=610 mm进口截面,稳定进料条件下壁面处的切向速度略大于脉动进料时的切向速度,此时稳定进料条件下的流场更适合进行气液分离。脉动进料条件下3个不同截面在在靠近中心点附近的切向速度值均小于稳定进料下的切向速度值,从气相分离角度来说,空气柱附近的气相切向速度越低,中心点的气相更易分离。
|
| 图 10 2种不同进料条件下分离器内部切向速度变化 Fig.10 Variation of tangential velocity inside the separator under two different feeding conditions |
| |
通过Fluent对旋流分离器的模拟仿真,对2种进料状态下的流场进行分析对比可得到如下结论。
1) 通过稳定进料条件下的气液旋流器仿真模拟,优选出溢流管直径68 mm,溢流管深度160 mm,入口截面积60×35 mm2,锥角度数14°等最适宜结构参数,在空气比例0.4,底流背压900 Pa的操作参数下会有最高分离效率98.2%。
2) 脉动进料条件下选用正弦波形作为脉冲波形较好。相同的其他参数条件下,采用频率为0.4 Hz的正弦脉冲进料时,旋流分离器的分离效率最高,可达85.5%,脉动进料使分离器的分离效率比稳定进料有所降低。
3) 通过稳定进料和脉动进料下的流体运动轨迹云图发现2者运动轨迹相似,运动迹线清晰,无紊乱流和逆流,在脉动进料条件下流场能实现良好的稳定性。对比2者的气相体积分布云图得到相似的呈中心对称分布规律,气液分离效果良好。
4) 通过进一步对比2种进料状态下流场参数的变化,相比于稳定进料状态,脉动进料时其内部湍流动能均值和幅值增大、切向速度均值和幅值降低、径向压力降梯度降低,上述参数变化是导致脉动进料气液效率降低的主要原因之一。
| [1] |
MELHUS T, MOWREY C, VASSHUS J K, et al. Intelligent, automated shale conveyance: Rotary screen vacuum assisted gas and solids separation system for drilling fluids[C]//2010 AADE Fluids Conference and Exhibition, Houston, Texas: 2010
|
| [2] |
丹尼尔·盖·波默洛. 用于干燥钻探切削物的真空系统和方法的优化: CN105498339A[P]. 2018-03-02 POMERLEAU Daniel Guy. Optimization of vacuum systems and methods for drying drill cuttings: CN105498339A[P]. 2016-03-02 (in Chinese) |
| [3] |
侯勇俊, 王钰文, 方潘, 等. 脉动负压振动设备: CN106194084B[P]. 2019-12-27 HOU Yongjun, WANG Yuwen, FANG Pan, et al. Pulse negative pressure vibrating equipment: CN106194084B[P]. 2019-12-27 (in Chinese) |
| [4] |
侯勇俊, 李芬. 脉冲气液喷射器基本性能的研究[J]. 工程热物理学报, 2020, 41(7): 1649-1659. HOU Yongjun, LI Fen. Study on basic performance of pulsed gas-liquid ejector[J]. Journal of Engineering Thermophysics, 2020, 41(7): 1649-1659. (in Chinese) |
| [5] |
侯勇俊, 李芬, 吴先进, 等. 负压钻井液振动筛气液喷射器性能的数值模拟研究[J]. 工程设计学报, 2019, 26(4): 423-432. HOU Yongjun, LI Fen, WU Xianjin, et al. Numerical simulation study of the performance of gas-liquid ejector in negative pressure drilling fluid shale shaker[J]. Chinese Journal of Engineering Design, 2019, 26(4): 423-432. DOI:10.3785/j.issn.1006-754X.2019.04.008 (in Chinese) |
| [6] |
杨兆铭, 陈建磊, 韩云蕊, 等. 二级旋流气液分离装置设计与流场特性模拟[J]. 过程工程学报, 2018, 18(6): 1198-1209. YANG Zhaoming, CHEN Jianlei, HAN Yunrui, et al. Design of two-stage swirling gas-liquid separator and simulation of flow field characteristics[J]. The Chinese Journal of Process Engineering, 2018, 18(6): 1198-1209. (in Chinese) |
| [7] |
左鹏, 姚秀颖, 卢春喜. 多旋臂气液旋流分离器内气相流动特性分析[J]. 过程工程学报, 2021, 21(9): 1042-1053. ZUO Peng, YAO Xiuying, LU Chunxi. Analysis on gas-phase flow characteristics in multi-spiral gas-liquid vortex separator[J]. The Chinese Journal of Process Engineering, 2021, 21(9): 1042-1053. (in Chinese) |
| [8] |
刘彩玉, 张爽, 耿海洋, 等. 同向出流气液分离器流场分析及结构参数优选[J]. 石油机械, 2020, 48(2): 90-96. LIU Caiyu, ZHANG Shuang, GENG Haiyang, et al. Flow field analysis and parameters optimization of a co-rotating outflow gas-liquid separation hydrocyclone[J]. China Petroleum Machinery, 2020, 48(2): 90-96. (in Chinese) |
| [9] |
CHU K, CHEN J, YU A B, et al. Numerical studies of multiphase flow and separation performance of natural medium cyclones for recovering waste coal[J]. Powder Technology, 2017, 314: 532-541. DOI:10.1016/j.powtec.2016.10.047 |
| [10] |
LIU S, YAN Y, GAO Y. Optimization of geometry parameters with separation efficiency and flow split ratio for downhole oil-water hydrocyclone[J]. Thermal Science and Engineering Progress, 2018, 8: 370-374. DOI:10.1016/j.tsep.2018.08.011 |
| [11] |
KAYA F, KARAGOZ I. Performance analysis of numerical schemes in highly swirling turbulent flows in cyclones[J]. Current Science, 2008, 94(10): 1273-1278. |
| [12] |
王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
| [13] |
[美] TU J, YEOH G H, LIU C著; 王晓冬译. 计算流体力学: 从实践中学习: A practical approach[M]. 沈阳: 东北大学出版社, 2009
|
| [14] |
WANG C, JI C, ZOU J. Simulation and experiment on transitional behaviours of multiphase flow in a hydrocyclone[J]. The Canadian Journal of Chemical Engineering, 2015, 93(10): 1802-1811. DOI:10.1002/cjce.22274 |
| [15] |
朱红钧, 林元华, 谢龙汉. FLUENT流体分析及仿真实用教程[M]. 北京: 人民邮电出版社, 2010.
|
| [16] |
庞学诗. 水力旋流器技术与应用[M]. 北京: 中国石化出版社, 2011.
|
| [17] |
闫雄雄, 李承溥. 水力旋流器结构参数对分离性能的影响分析[J]. 石油化工设备, 2011, 40(S2): 70-72. YAN Xiongxiong, LI Chengpu. Analysis of the influence of hydrocyclone structure parameters on separation performance[J]. Petro-Chemical Equipment, 2011, 40(S2): 70-72. (in Chinese) |
| [18] |
邱良燕, 戴石良, 李贝贝, 等. 新型旋流分离器的结构优化与实验研究[J]. 化学工程, 2020, 48(10): 63-67, 78. QIU Liangyan, DAI Shiliang, LI Beibei, et al. Structural optimization and experimental study of new cyclone separator[J]. Chemical Engineering (China), 2020, 48(10): 63-67, 78. (in Chinese) |
| [19] |
LI W, WU X, ZHANG D, et al. Preliminary study of coupling CFD code FLUENT and system code RELAP5[J]. Annals of Nuclear Energy, 2014, 73: 96-107. |
| [20] |
RYBDYLOVA O, POULTON L, QUBEISSI M A, et al. A model for multi-component droplet heating and evaporation and its implementation into ANSYS Fluent[J]. International Communications in Heat and Mass Transfer, 2018, 90: 29-33. DOI:10.1016/j.icheatmasstransfer.2017.10.018 |
| [21] |
辛颖. Fluent UDF方法在数值波浪水槽中的应用研究[D]. 辽宁大连: 大连理工大学, 2013 XIN Ying. Application of fluent udf method in the study of numerical wave tank[D]. Liaoning Dalian: Dalian University of Technology, 2013 (in Chinese) |
| [22] |
胡坤, 胡婷婷, 马海峰. ANSYS Fluent实例详解[M]. 北京: 机械工业出版社, 2019.
|
| [23] |
金雪菲. 液液两相分离装置结构研究与流场分析研究[D]. 杭州: 浙江大学, 2011 JIN Xuefei. Flow field research and structure research of liquid-liquid separator[D]. Hangzhou: Zhejiang University, 2011: 35-70(in Chinese) |
| [24] |
FENG J, TANG X, WANG W, et al. A combined method in parameters optimization of hydrocyclone[J]. Mathematical Problems in Engineering, 2016. DOI:10.1155/2016/9209362 |
 2022, Vol. 39
2022, Vol. 39





